Sequential k-Means Clustering
Another way to modify the k-means procedure is
to update the means one example at a time, rather than all at once. This
is particularly attractive when we acquire the examples over a period of
time, and we want to start clustering before we have seen all of the examples.
Here is a modification of the k-means procedure that operates sequentially:
- Make initial guesses for the means m1,
m2, ..., mk
- Set the counts n1, n2, ..., nk to
zero
- Until interrupted
- Acquire the next example, x
- If mi is closest to x
- Increment ni
- Replace mi by mi
+ (1/ni)*( x - mi)
- end_if
- end_until
It is a good exercise to show that the resulting mi
is the average of all of the examples x that were closest
to mi when they were acquired.
This also suggests another alternative in which we replace the counts by
constants. In particular, suppose that a is a constant between 0 and 1,
and consider the following variation:
- Make initial guesses for the means m1,
m2, ..., mk
- Until interrupted
- Acquire the next example, x
- If mi is closest to x
, replace mi by mi
+ a*( x - mi )
- end_until
Electrical engineers familiar with DSP will say that we have replaced an
averaging operation by a low-pass-filtering operation. The result might
be called the "forgetful" sequential k-means
procedure. It is not hard to show that mi is a weighted
average of the examples that were closest to mi,
where the weight decreases exponentially with the "age" to the
example. To be more precise, if mo is the initial
value of mi and if xj
is the jth of n examples that were used to form mi,
then it is not hard to show that
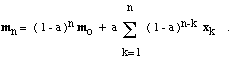
Thus, the initial value mo is eventually
forgotten, and recent examples receive more weight than ancient examples.
This variation of k-means is particularly simple to implement, and it is
attractive when the nature of the problem changes over time and the cluster
centers "drift." It also leads naturally to the idea of self-organizing
feature maps.
 Back to Fuzzy k-Means
Back to Fuzzy k-Means
 On to SOFM
On to SOFM  Up to Clustering
Up to Clustering
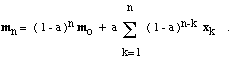
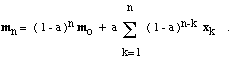
![]() Back to Fuzzy k-Means
Back to Fuzzy k-Means
![]() On to SOFM
On to SOFM ![]() Up to Clustering
Up to Clustering