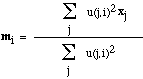The Fuzzy-k-Means Procedure

The clusters produced by the k-means procedure are sometimes called "hard" or "crisp" clusters, since any feature vector x either is or is not a member of a particular cluster. This is in contrast to "soft" or "fuzzy" clusters, in which a feature vector x can have a degree of membership in each cluster.* The fuzzy-k-means procedure of Dunn and Bezdek (see Bezdek) allows each feature vector x to have a degree of membership in Cluster i:

Make initial guesses for the means m₁, m₂,..., m_k
Until there are no changes in any mean:
- Use the estimated means to find the degree of membership u(j,i) of x_j in Cluster i;
  for example, if a(j,i) = exp(- || x_j - m_i ||²), one might use u(j,i) = a(j,i) / sum_j a(j,i)
- For i from 1 to k
  - Replace m_i with the fuzzy mean of all of the examples for Cluster i --
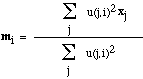
- end_for
end_until

For those who are interested, there are a number of ways to generalize this procedure further (see Bezdek). It has the advantage that it more naturally handles situations in which subclasses are formed by mixing or interpolating between extreme examples, so that it makes more sense to say that x is 40% in Cluster 1 and 60% in Cluster 2, rather than having to assign x completely to one cluster or the other.
________
* In the case of the fuzzy-k-means procedure, the degree of membership can also be interpreted probabilistically as the square root of the a posteriori probability the x is in Cluster i. See Duda and Hart, Section 6.4.

Back to k-means

On to Sequential

Up to Clustering