 K-d Trees
K-d Trees
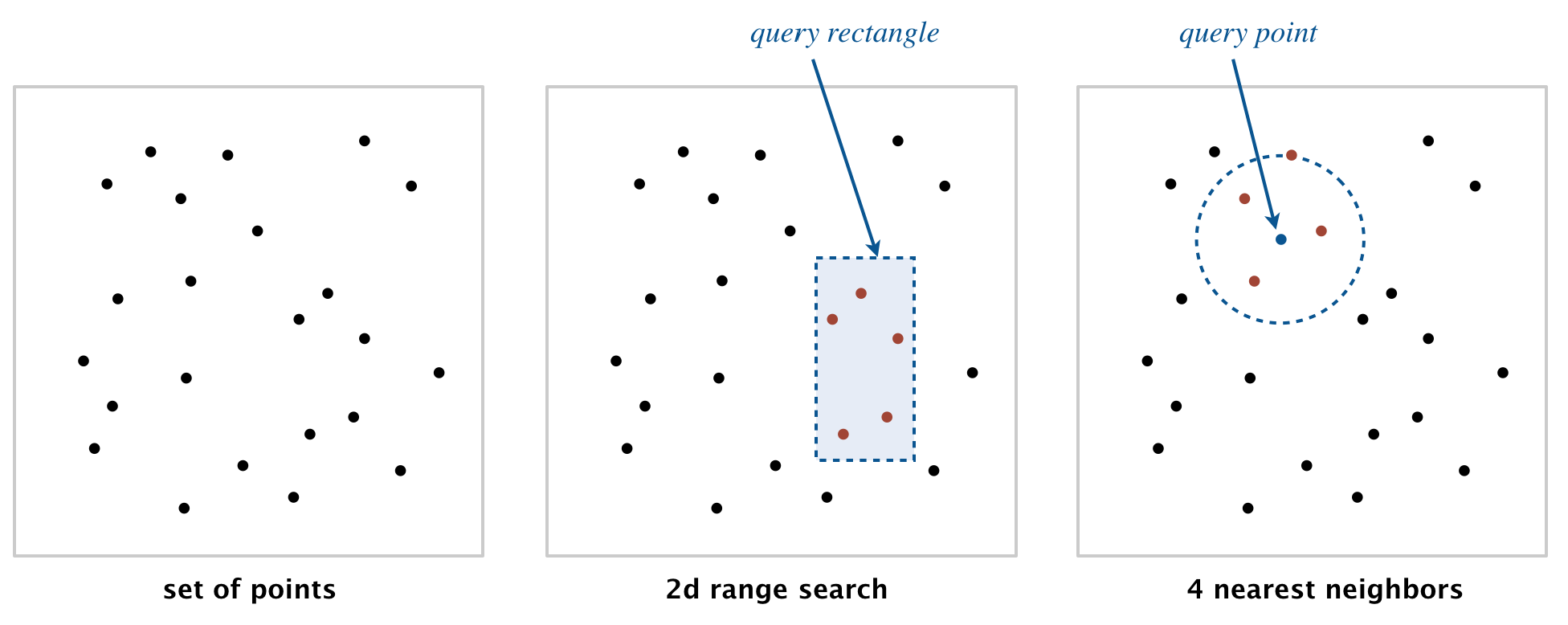
Geometric primitives.
To get started, use the following geometric primitives for points and
axis-aligned rectangles in the plane.
algs4.jar) represents points in the plane.
Here is the subset of its API that you may use:
public class Point2D implements Comparable<Point2D> {
// construct the point (x, y)
public Point2D(double x, double y)
// x-coordinate
public double x()
// y-coordinate
public double y()
// square of Euclidean distance between two points
public double distanceSquaredTo(Point2D that)
// for use in an ordered symbol table
public int compareTo(Point2D that)
// does this point equal that object?
public boolean equals(Object that)
// string representation with format (x, y)
public String toString()
}
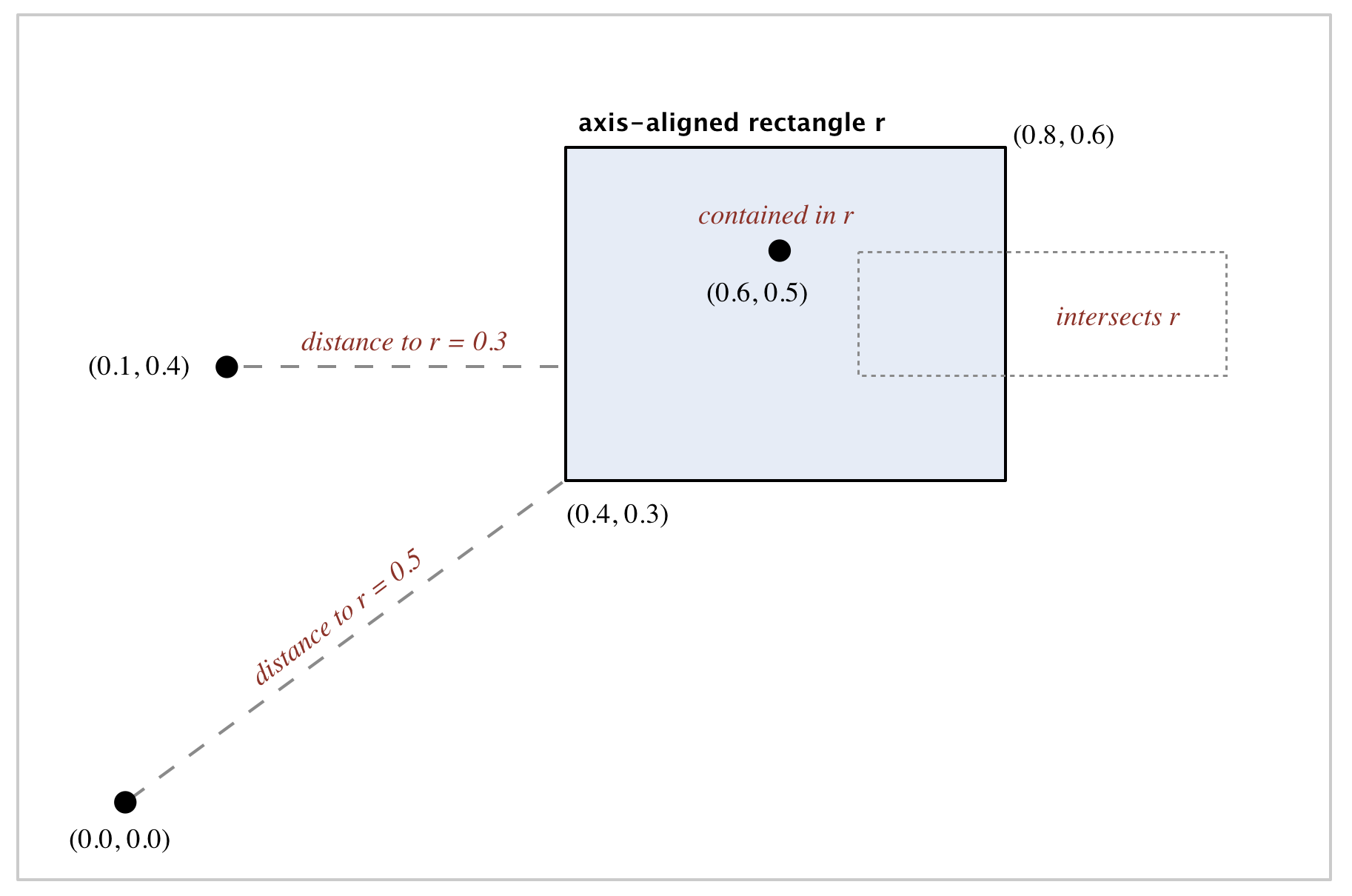
algs4.jar) represents axis-aligned rectanges.
Here is the subset of its API that you may use:
public class RectHV {
// construct the rectangle [xmin, xmax] x [ymin, ymax]
public RectHV(double xmin, double ymin, double xmax, double ymax)
// minimum x-coordinate of rectangle
public double xmin()
// minimum y-coordinate of rectangle
public double ymin()
// maximum x-coordinate of rectangle
public double xmax()
// maximum y-coordinate of rectangle
public double ymax()
// does this rectangle contain the point p (either inside or on boundary)?
public boolean contains(Point2D p)
// does this rectangle intersect that rectangle (at one or more points)?
public boolean intersects(RectHV that)
// square of Euclidean distance from point p to closest point in rectangle
public double distanceSquaredTo(Point2D p)
// does this rectangle equal that object?
public boolean equals(Object that)
// string representation with format [xmin, xmax] x [ymin, ymax]
public String toString()
}
Brute-force implementation.
Write a mutable data type PointST.java that uses a red–black BST to
represent a symbol table whose keys are two-dimensional points, by implementing the following API:
public class PointST<Value> {
// construct an empty symbol table of points
public PointST()
// is the symbol table empty?
public boolean isEmpty()
// number of points
public int size()
// associate the value val with point p
public void put(Point2D p, Value val)
// value associated with point p
public Value get(Point2D p)
// does the symbol table contain point p?
public boolean contains(Point2D p)
// all points in the symbol table
public Iterable<Point2D> points()
// all points that are inside the rectangle (or on the boundary)
public Iterable<Point2D> range(RectHV rect)
// a nearest neighbor of point p; null if the symbol table is empty
public Point2D nearest(Point2D p)
// unit testing (required)
public static void main(String[] args)
}
Implementation requirements.
You must use either
RedBlackBST or
java.util.TreeMap;
do not implement your own red–black BST.
Corner cases.
Throw an IllegalArgumentException if any argument is null.
Unit testing.
Your main() method must call each public constructor and method directly and
help verify that they work as prescribed (e.g., by printing results to standard output).
Performance requirements.
In the worst case, your implementation must support size() in constant time;
put(), get() and contains() in \(\Theta(\log n\)) time;
and points(), nearest(), and range()
in \(\Theta(n)\) time,
where n is the number of points in the symbol table.
2d-tree implementation.
Write a mutable data type KdTreeST.java that uses a 2d-tree to
implement the same API (but renaming PointST to KdTreeST).
A 2d-tree is a generalization of a BST to two-dimensional keys.
The idea is to build a BST with points in the nodes,
using the x- and y-coordinates of the points
as keys in strictly alternating sequence, starting with the x-coordinates.
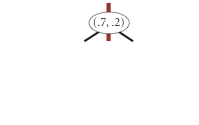
insert (0.7, 0.2) 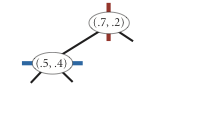
insert (0.5, 0.4) 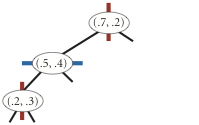
insert (0.2, 0.3) 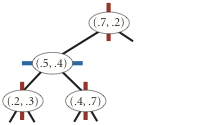
insert (0.4, 0.7) 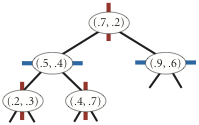
insert (0.9, 0.6)
points() method must return the points in level order:
first the root, then all children of the root (from left/bottom to right/top),
then all grandchildren of the root (from left to right), and so forth.
The level-order traversal of the above 2d-tree is
(0.7, 0.2), (0.5, 0.4), (0.9, 0.6), (0.2, 0.3), (0.4, 0.7).
This method is useful to assist you (when debugging) and
us (when grading).
The prime advantage of a 2d-tree over a BST is that it supports efficient implementation of range search and nearest-neighbor search. Each node corresponds to an axis-aligned rectangle, which encloses all of the points in its subtree. The root corresponds to the entire plane [(−∞, −∞), (+∞, +∞ )]; the left and right children of the root correspond to the two rectangles split by the x-coordinate of the point at the root; and so forth.
Clients. You may use the following two interactive client programs to test and debug your code.
Analysis of running time. Analyze the effectiveness of your approach to this problem by estimating how many many nearest-neighbor searches per second that each of your two implementations can perform for input1M.txt (1 million points), where the query points are uniformly random points in the unit square. Count only the time for the nearest-neighbor searches, not the time to read and insert the points.
Challenge for the bored. Add the following method
to KdTreeST.java:
This method returns the k points that are closest to the query point (in any order); return all n points in the data structure if n ≤ k. It must do this in an efficient manner, i.e. using the technique from k-d tree nearest neighbor search, not from brute force. Once you’ve completed this class, you’ll be able to run BoidSimulator.java (which depends upon both Boid.java and Hawk.java). Behold their flocking majesty.public Iterable<Point2D> nearest(Point2D p, int k)
Submission.
Submit only PointST.java and KdTreeST.java.
We will supply algs4.jar.
You may not call library functions except those in
those in java.lang, java.util, and algs4.jar.
Finally, submit readme.txt
and acknowledgments.txt
files and answer the questions.
Grading.
file points PointST.java10 KdTreeST.java24 readme.txt6 40
Reminder: You can lose up to 4 points for poor style
and up to 4 points for inadequate unit testing.