 K-d Trees
K-d Trees
What should I do if a point is inserted twice in the data structure? The data structure represents a symbol table, so you should replace the old value with the new value.
How do I return an Iterable<Point2D>?
Add the Point2D objects you want to a Stack<Point2D> or
Queue<Point2D>
and return that.
Of course, your client code should not depend on whether the iterable returned
is a stack or queue (because it could be any iterable).
What should points() return if there are no points in the data structure?
What should range() return if there are no points in the range?
The API says to return an Iterable<Point2D>, so you should return
an iterable with zero points.
What should nearest() return if there are two (or more) nearest points?
The API does not specify, so you may return
any nearest point (up to floating-point precision).
I run out of memory when running some of the large sample files. What should I do?
Be sure to ask Java for additional memory,
e.g., java-algs4 -Xmx1600m RangeSearchVisualizer input1M.txt.
Can I use the distanceTo() method in Point2D and RectHV?
No, you may use only the subset of the methods listed in the assignment specification.
You should be able to accomplish
the same result (more efficiently) with distanceSquaredTo().
Can I use the X_ORDER() and Y_ORDER() comparators
in Point2D?
No, you may use only the subset of the methods listed in the assignment specification.
You should be able to accomplish
the same result by calling the methods x() and y().
Is a point on the boundary of a rectangle considered inside it? Do two rectangle intersect if they have just one point in common? Yes and yes. Here are the APIs for Point2D and RectHV.
How can I create a RectHV for the entire plane or a halfplane?
You can use the values
Double.POSITIVE_INFINITY or
Double.NEGATIVE_INFINITY for one (or more) of the coordinates when you
create a RectHV.
What does the notation [0.5, 0.75] × [0.25, 0.375] mean when specifying a rectangle?
It is the Cartesian product
of the x-interval [0.5, 0.75] and the y-interval [0.25, 0.375]:
the rectangle that includes all points with both 0.5 ≤ x ≤ 0.75
and 0.25 ≤ y ≤ 0.375.
Note that the arguments to the RectHV
constructor are in the order xmin, ymin, xmax, and ymax
but the toString() method uses the Cartesian product notation.
In which order should the points() method in PointST return the points?
The API does not specify the order, so any order is fine.
What makes KdTreeST difficult? How do I make the best use of my time? Debugging performance errors is one of the biggest challenges. It is very important that you understand and implement the key optimizations described in the assignment specification:
range() or nearest() until you understand these rules.
I'm nervous about writing recursive search tree code. How do I even start on KdTreeST.java?
Use BST.java as a guide.
The trickiest part is understanding how the put() method works. You do not need to
include code that involves storing the subtree sizes
(since this is used only for ordered symbol table operations).
Will I lose points for a non-recursive implementation of range search? No. While we recommend using a recursive implementation (both for elegance and as a warmup for nearest-neighbor search), you are free to implement it without using recursion.
What should I do if a point has the same x-coordinate as the point in a node when inserting or searching in a 2d-tree? Go to the right subtree as specified in the assignment under Search and insert.
Sample input files. Download kdtree.zip. It contains sample input files in the specified format.
Testing the bounding boxes.
If you include the RectHV bounding boxes in the k-d tree nodes,
you want to make sure that you got it right. Otherwise, the mistake might
not manifest itself until either range search and/or nearest neighbor search.
Here are the bounding boxes corresponding to the nodes in input5.txt:
toString() method format of RectHV
which is \([x_{min}, x_{max}] \; \times \; [y_{min}, y_{max}]\) instead of
\((x_{min}, y_{min})\) to \((x_{max}, y_{max})\).
Testing put() and points() in KdTreeST.
The client KdTreeVisualizer.java
reads a sequence of points from a file (given as a command-line argument) and
draws the corresponding k-d tree. It does so by reconstruting the k-d tree from
the level-order traversal returned by points().
Note that it assumes all points are inside the unit square.
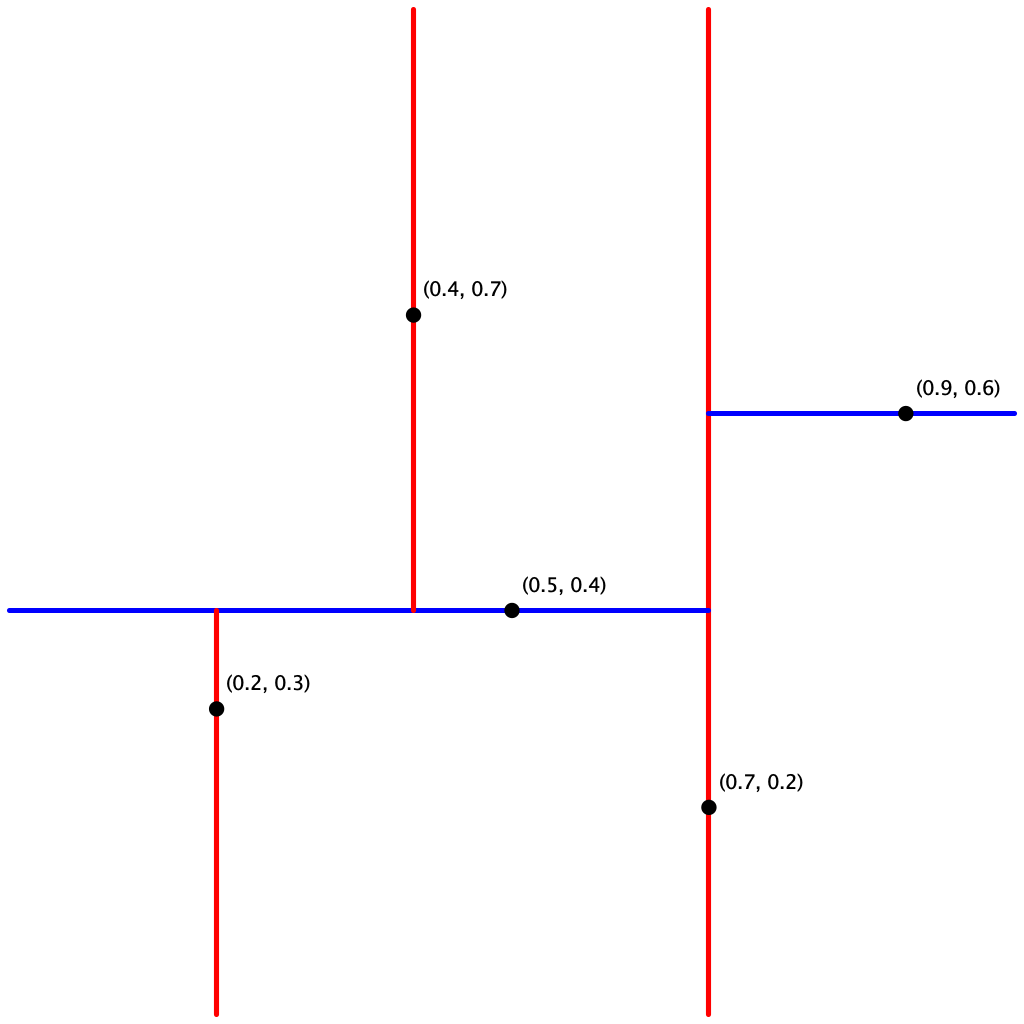
input5.txt 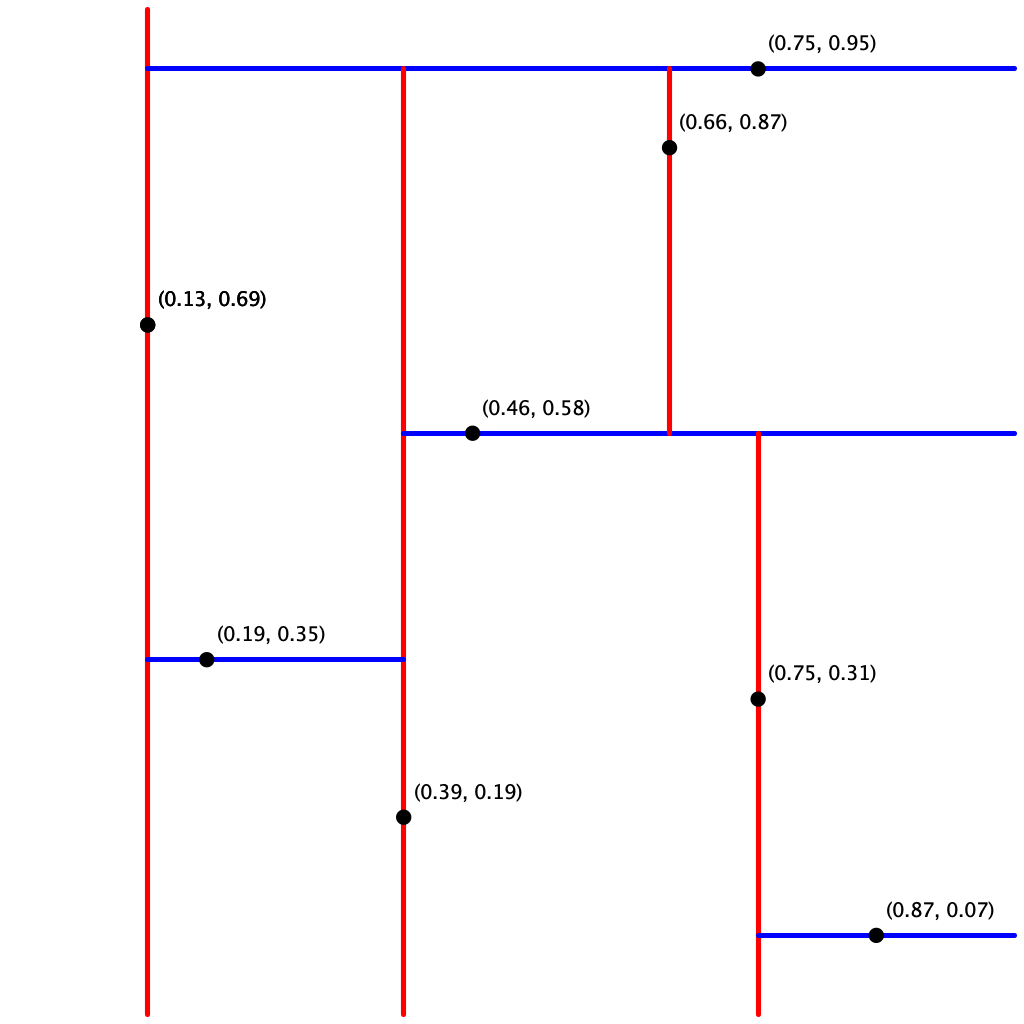
input8.txt 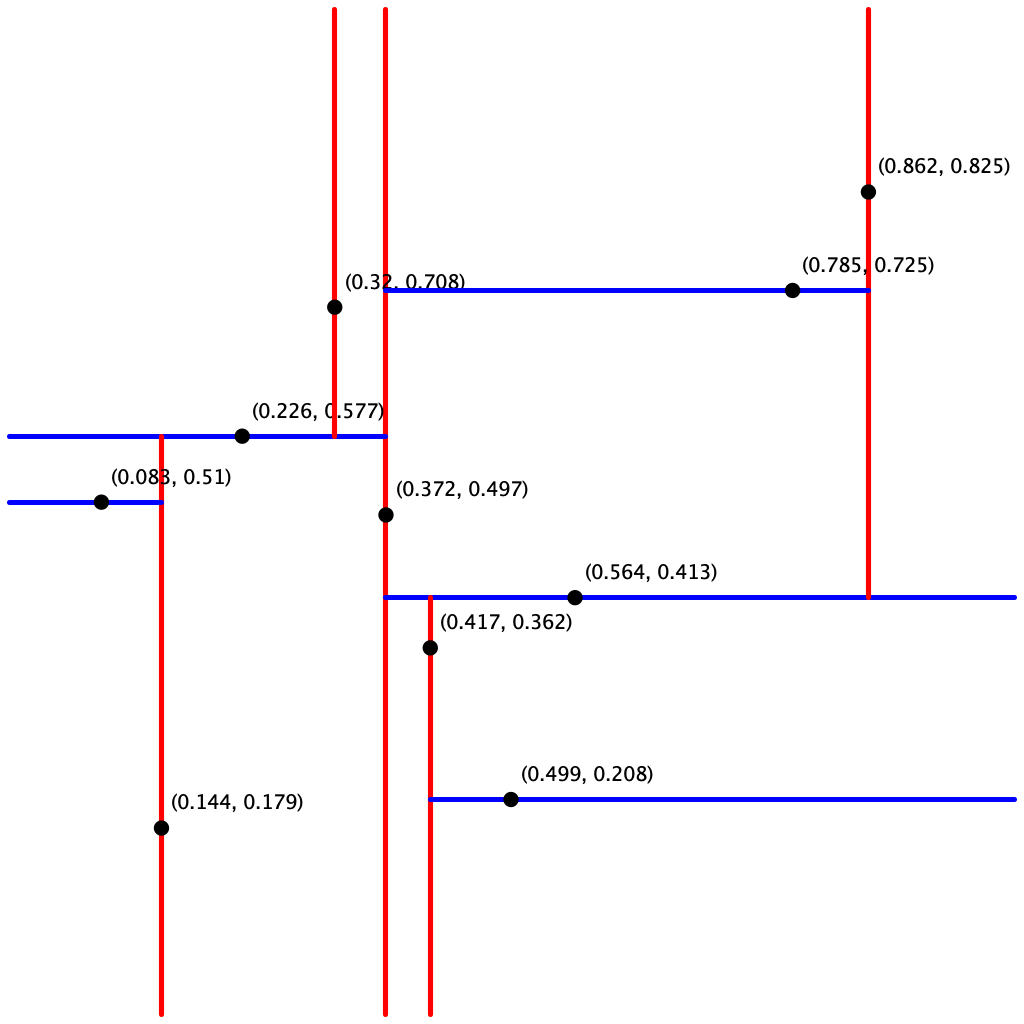
input10.txt
Testing range() and nearest() in KdTreeST.
A good way to test these methods is to perform
the same sequence of operations on both the PointST and
KdTreeST data types and identify any discrepancies.
The key is to implement a reference solution in which you have confidence.
The brute-force implementation PointST can serve this purpose
in your testing.
range() in PointST and blue the points returned by
the method range() in KdTreeST.
nearest() in PointST and blue the point returned by
the method nearest() in KdTreeST.
How do I measure the number of calls per second to nearest()?
Here is one reasonable approach.
input1M.txt and insert those 1 million points into the k-d tree.
nearest() with random points in the unit square.
nearest().
You can use Stopwatch or StopwatchCPU.
How do I generate a uniformly random point in the unit square?
Make two calls to StdRandom.uniformDouble(0.0, 1.0)—one for the x-coordinate
and one for the y-coordinate.
These are purely suggestions for how you might make progress on KdTreeST.java.
You do not have to follow these steps.
PointST. This should be straightforward if you use
either
RedBlackBST
or
TreeMap
and are familiar with the subset of the
Point2D
and
RectHV
APIs that you may use.
After completing this step, you are only about 15% done with the assignment.
private class Node {
private Point2D p; // the point
private Value val; // the symbol table maps the point to this value
private RectHV rect; // the axis-aligned rectangle corresponding to this node
private Node lb; // the left/bottom subtree
private Node rt; // the right/top subtree
}
isEmpty() and size(). These should be very easy.
put() which does everything except set up the
RectHV for each node. Write the get() and contains() method, and use these to test that
put() was implemented properly. Note that put() and get()
are best implemented by using private helper methods analogous to those found on page 399
and in BST.java.
We recommend using the orientation (vertical or horizontal) as an argument to these helper methods.
A common error is to not rely on your base case (or cases). For example, compare the following two
get() methods for searching in a BST:
private Value get(Node x, Key key) {
if (x == null) return null;
int cmp = key.compareTo(x.key);
if (cmp < 0) return get(x.left, key);
else if (cmp > 0) return get(x.right, key);
else return x.val;
}
private Value overlyComplicatedGet(Node x, Key key) {
if (x == null) return null;
int cmp = key.compareTo(x.key);
if (cmp < 0) {
if (x.left == null) return null;
else return overlyComplicatedGet(x.left, key);
}
else if (cmp > 0) {
if (x.right == null) return null;
else return overlyComplicatedGet(x.right, key);
}
else return x.val;
}
The second method performs extraneous null checks that would otherwise be caught by the
base case. When there are multiple base cases, these extraneous checks proliferate and
make your code harder to read, maintain, and debug. Trust in the base case.
points() method. Use this to check the structure of your
k-d tree.
put() which sets up the RectHV for each Node.
range() method.
Test your
implementation using RangeSearchVisualizer.java,
which is described in the testing section.
nearest() method. This is the hardest method. We
recommend doing it in stages.
Test your implementation using NearestNeighborVisualizer.java, which is described in the testing section.
These are many ways to improve performance of your 2d-tree. Here are some ideas.
distanceSquaredTo() but not distanceTo().
RectHV in each 2d-tree node (though it
is probably wise in your first version).