Invariant Linear Discriminants

There is an important special case in which the Mahalanobis metric again results in linear discriminant functions. This case occurs when the clusters in all c classes have the same covariance matrix C. Geometrically, this situation arises when the clusters for all of the categories have the same ellipsoidal shape. Physically, this situation arises when the problem is to detect one of c different signals in the presence of additive noise, where the noise does not depend upon which of the signals is present. In that case, we can expand the squared Mahalanobis distance from the feature vector x to the mean vector m_k as

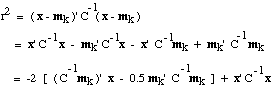
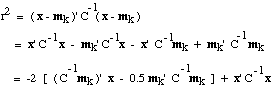
This should remind you of the similar expression we obtained for a minimum-Euclidean-distance classifier. Once again we can obtain linear discriminant functions by maximizing the expression in the brackets. This time we define the linear discriminant function g(x_k) by

where

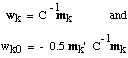
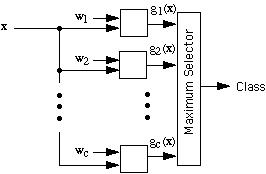
This result is very useful. Although it gives up the advantages of having curved decision boundaries, it retains the advantages of being invariant to linear transformations. In addition, it reduces the memory requirements from the c d-by-d covariance matrices to the c d-by 1 weight vectors w₁, w₂, ... , w_c, with a corresponding speed-up in the computation of the discriminant functions. Finally, when the covariance matrices are the same for all c classes, one can pool the data from all the classes and get a much better results from a limited amount of data.

Back to Metric Up to Mahalanobis