is called the Mahalanobis distance from the feature
vector x to the mean vector mx, where
Cx is the covariance matrix for x.
It can be shown that the surfaces on which r is constant are ellipsoids
that are centered about the mean mx. In the special case
where the features are uncorrelated and the variances in all directions
are the same, these surfaces are spheres, and the Mahalanobis distance becomes
equivalent to the Euclidean distance.
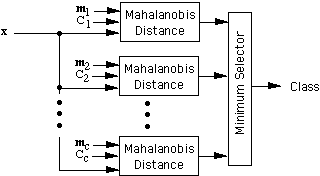
One can use the Mahalanobis distance in a minimum-distance classifier as
follows. Let m1, m2, ... , mc be the means (templates) for the c classes, and let C1, C2, ... , Cc be
the corresponding covariance matrices. We classify a feature vector x
by measuring the Mahalanobis distance from x to each of
the means, and assigning x to the class for which the Mahalanobis
distance is minimum.
The use of the Mahalanobis metric removes several of the limitations of the Euclidean metric:
However, there is a price to be paid for these advantages. The covariance matrices can be hard to determine accurately, and the memory and time requirements grow quadratically rather than linearly with the number of features. These problems may be insignificant when only a few features are needed, but they can become quite serious when the number of features becomes large.
- It automatically accounts for the scaling of the coordinate axes
- It corrects for correlation between the different features
- It can provide curved as well as linear decision boundaries