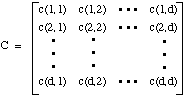
All of the covariances c(i,j) can be collected together into a covariance matrix C:
Covariance Matrix
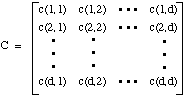
This matrix provides us with a way to measure distance that is invariant
to linear transformations of the data. Suppose that we start with a d-dimensional
feature vector x that has a mean vector mx
and a covariance matrix Cx. If we use the d-by-d matrix A to
transform x into y through
it is not hard to show that the mean vector for y is
given by
and the covariance matrix for y is given by
Suppose now that we want to measure the distance from x
to mx, or from y to my.
We could, of course, use the Euclidean norm, but it would be very unusual
if the Euclidean distance from x to mx
turned out to be the same as the Euclidean distance from y
to my. (Geometrically, that would happen only
if A happened to correspond to a rotation or a reflection, which is not
very interesting.) What we want to do is to normalize the distance, much
like we did when we defined the standardized distance
for a single feature. The question is: What is the matrix generalization
of the scalar expression
The answer turns out to be
If you know some linear algebra, you should be able to prove that this
expression is invariant to any nonsingular linear transformation. That is,
if you substitute y = A x and use the
formulas above for my and Cy, you
will get the very same numerical value for r, no matter what the matrix
A is.*
Now, suppose there is a feature space in which the clusters are spherical
and the Euclidean metric provides the right way to measure the distance
from y to my. In that space,
the covariance matrix is the identity matrix, and r is exactly the Euclidean
distance from y to my. But
since we can get to that space from the x space through
a linear transformation, and since r is invariant to linear transformation,
we can equally well compute r directly from