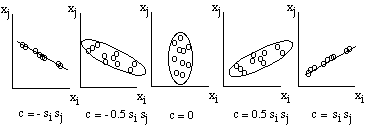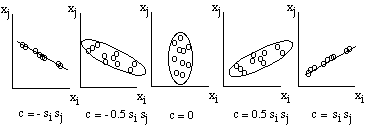Covariance
The covariance of two features measures their tendency to vary together,
i.e., to co-vary. Where the variance is the average of the squared deviation
of a feature from its mean, the covariance is the average of the products
of the deviations of feature values from their means.
To be more precise, consider Feature i and Feature j. Let { x(1,i), x(2,i),
... , x(n,i) } be a set of n examples of Feature i, and let { x(1,j), x(2,j),
... , x(n,j) } be a corresponding set of n examples of Feature j. (That
is, x(k,i) and x(k,j) are features of the same pattern, Pattern k.) Similarly,
let m(i) be the mean of Feature i, and m(j) be the mean of Feature j. Then
the covariance of Feature i and Feature j is defined by
c(i,j) = { [ x(1,i) - m(i) ] [ x(1,j) - m(j) ] + ... + [ x(n,i)
- m(i) ] [ x(n,j) - m(j) ] } / ( n - 1 ) .
The covariance has several important properties:
- If Feature i and Feature j tend to increase together, then c(i,j)
> 0
- If Feature i tends to decrease when Feature j increases, then c(i,j)
< 0
- If Feature i and Feature j are independent, then c(i,j) = 0 *
- | c(i,j) | <= s(i) s(j), where s(i) is the standard deviation of
Feature i
- c(i,i) = s(i)2 = v(i)
Thus, the covariance c(i,j) is a number between - s(i) s(j) and + s(i) s(j)
that measures the dependence between Feature i and Feature j, with c(i,j)
= 0 if there is no dependence. The correspondence between the covariance
and the shape of the data cluster is illustrated below.
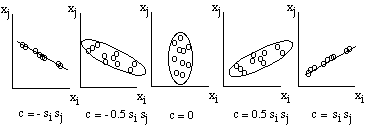
Back to Linear
On to Matrix
Up to Mahalanobis