Linear Discriminants

Recall that when we use a minimum-distance classifier to classify a feature vector x, we measure the distance from x to the templates m₁, m₂, ..., m_c and assign x to the class of the nearest template. Using the inner product to express the Euclidean distance from x to m_k, we can write

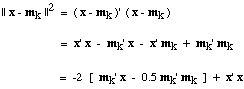
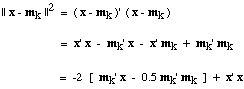
Notice that the x'x term is the same for every class, i.e., for every k. To find the template m_k that minimizes || x - m_k ||, it is sufficient to find the m_k that maximizes the bracketed expression, m_k' x - 0.5 m_k' m_k. Let us define the linear discriminant function g(x) by

g(x) = m' x - 0.5 || m ||² .

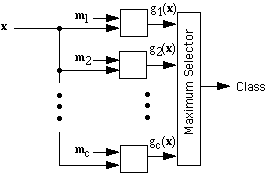
Then we can say that a minimum-Euclidean-distance clasifier classifies an input feature vector x by computing c linear discriminant functions g₁(x), g₂(x), ... , g_c(x) and assigning x to the class corresponding to the maximum discriminant function. We can also think of the linear discriminant functions as measuring the correlation between x and m_k, with the addition of a correction for the "template energy" represented by || m_k ||². With this correction included, a minimum-Euclidean-distance classifier is equivalent to a maximum-correlation classifier.

Back to Inner Prod. On to Boundaries Up to Simple Classifiers