Decision Boundaries

In general, a pattern classifier carves up (or tesselates or partitions) the feature space into volumes called decision regions. All feature vectors in a decision region are assigned to the same category. The decision regions are often simply connected, but they can be multiply connected as well, consisting of two or more non-touching regions.

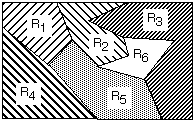
The decision regions are separated by surfaces called the decision boundaries. These separating surfaces represent points where there are ties between two or more categories.

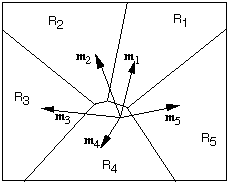
For a minimum-distance classifier, the decision boundaries are the points that are equally distant from two or more of the templates. With a Euclidean metric, the decision boundary between Region i and Region j is on the line or plane that is the perpendicular bisector of the line from m_i to m_j. Analytically, these linear boundaries are a consequence of the fact that the discriminant functions are linear. (With the Mahalanobis metric, the decision boundaries are quadratic surfaces, such as ellipsoids, paraboloids or hyperboloids.)

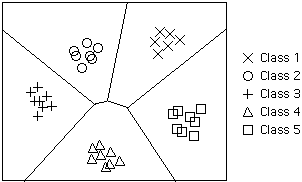
Nearest-template decision boundaries

How well the classifier works depends upon how closely the input patterns to be classified resemble the templates. In the example sketched below, the correspondence is very close, and one can anticipate excellent performance. However, things are not always this good in practice, and one should understand the limitations of simple classifiers.

Back to Linear Up to Simple Classifiers