Slider Puzzle Assignment

Write a program to solve the 8-puzzle problem (and its natural generalizations) using the A* search algorithm.

The problem. The 8-puzzle is a sliding puzzle that is played on a 3-by-3 grid with 8 square tiles labeled 1 through 8, plus a blank square. The goal is to rearrange the tiles so that they are in row-major order, using as few moves as possible. You are permitted to slide tiles either horizontally or vertically into the blank square. The following diagram shows a sequence of moves from an initial board (left) to the goal board (right).

Board data type. To begin, create a data type that models an n-by-n board with sliding tiles. Implement an immutable data type Board with the following API:

public class Board {

    // create a board from an n-by-n array of tiles,
    // where tiles[row][col] = tile at (row, col)
    public Board(int[][] tiles)
                                           
    // string representation of this board
    public String toString()

    // tile at (row, col) or 0 if blank
    public int tileAt(int row, int col)

    // board size n
    public int size()

    // number of tiles out of place
    public int hamming()

    // sum of Manhattan distances between tiles and goal
    public int manhattan()

    // is this board the goal board?
    public boolean isGoal()

    // does this board equal y?
    public boolean equals(Object y)

    // all neighboring boards
    public Iterable<Board> neighbors()

    // is this board solvable?
    public boolean isSolvable()

    // unit testing (required)
    public static void main(String[] args)

}

Constructor. You may assume that the constructor receives an n-by-n array containing a permutation of the n² integers between 0 and n² − 1, where 0 represents the blank square. You may also assume that 2 ≤ n ≤ 32,768.

String representation. The toString() method returns a string composed of n + 1 lines. The first line contains the board size n; the remaining n lines contains the n-by-n grid of tiles in row-major order, using 0 to designate the blank square.

Tile extraction. Throw an IllegalArgumentException in tileAt() unless both row and col are between 0 and n − 1.

Hamming and Manhattan distances. To measure how close a board is to the goal board, we define two notions of distance. The Hamming distance between a board and the goal board is the number of tiles in the wrong position. The Manhattan distance between a board and the goal board is the sum of the Manhattan distances (sum of the vertical and horizontal distance) from the tiles to their goal positions.

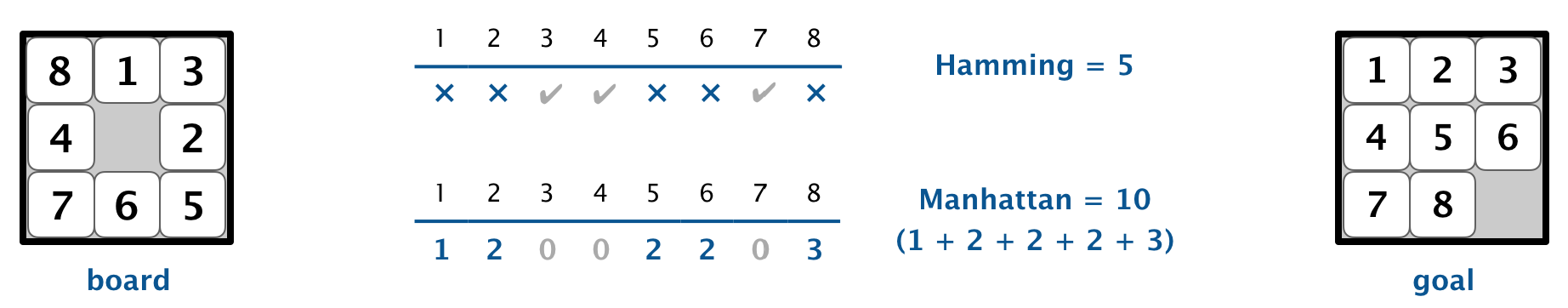
Comparing two boards for equality. Two boards are equal if they are have the same size and their corresponding tiles are in the same positions. The equals() method is inherited from java.lang.Object, so it must obey all of Java’s requirements.

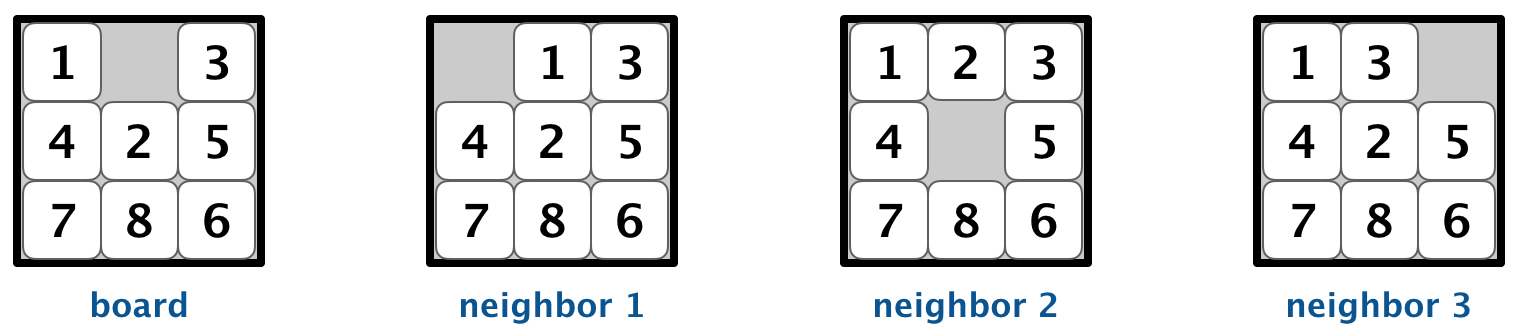
Neighboring boards. The neighbors() method returns an iterable containing the neighbors of the board. Depending on the location of the blank square, a board can have 2, 3, or 4 neighbors.

Detecting unsolvable boards. An efficient approach for detecting unsolvable boards is described in the next section.

Unit testing. Your main() method must call each public method directly and help verify that they works as prescribed (e.g., by printing results to standard output).

Performance requirements. Your implementation must achieve the following worst-case performance requirements:

The size() and tileAt() methods must take constant time.
The hamming(), manhattan(), and isGoal() methods must take constant time. See the optimizations section for more information.
The constructor, equals(), toString(), and neighbors() methods must take \(O(n^2)\) time.
The isSolvable() method must take \(O(n^4)\) time.

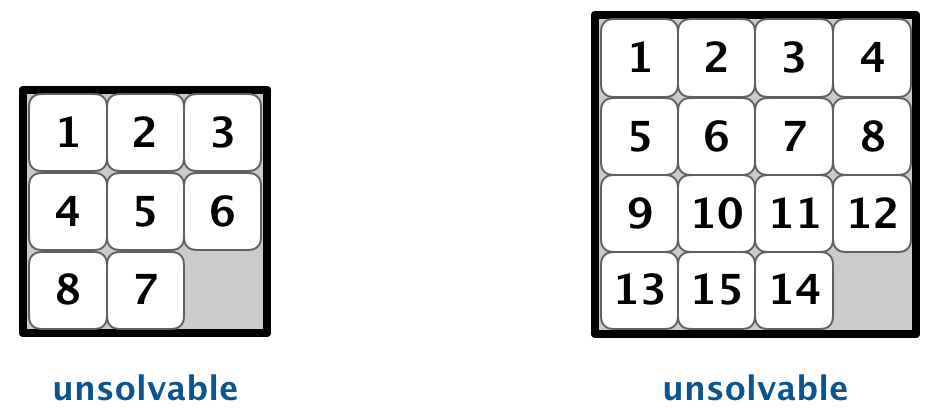
Detecting unsolvable boards. Not all initial boards can lead to the goal board by a sequence of moves, including these two:

Remarkably, we can determine whether a board is solvable without solving it! To do so, we count inversions, as described next.

Inversions. Given a board, an inversion is any pair of tiles i and j where i < j but i appears after j when considering the board in row-major order (row 0, followed by row 1, and so forth).
Odd-sized boards. First, we’ll consider the case when the board size n is an odd integer. In this case, each move changes the number of inversions by an even number. Thus, if a board has an odd number of inversions, it is unsolvable because the goal board has an even number (zero) of inversions.

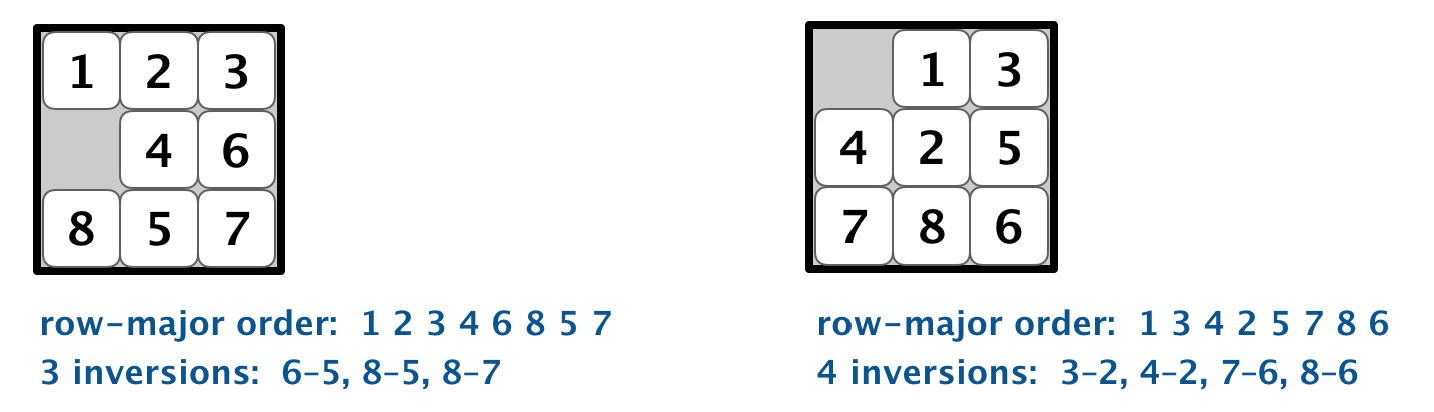
It turns out that the converse is also true: if a board has an even number of inversions, then it is solvable.

In summary, when n is odd, an n-by-n board is solvable if and only if its number of inversions is even.
Even-sized boards. Now, we’ll consider the case when the board size n is an even integer. In this case, the parity of the number of inversions is not invariant. However, the parity of the number of inversions plus the row of the blank square (indexed starting at 0) is invariant: each move changes this sum by an even number.

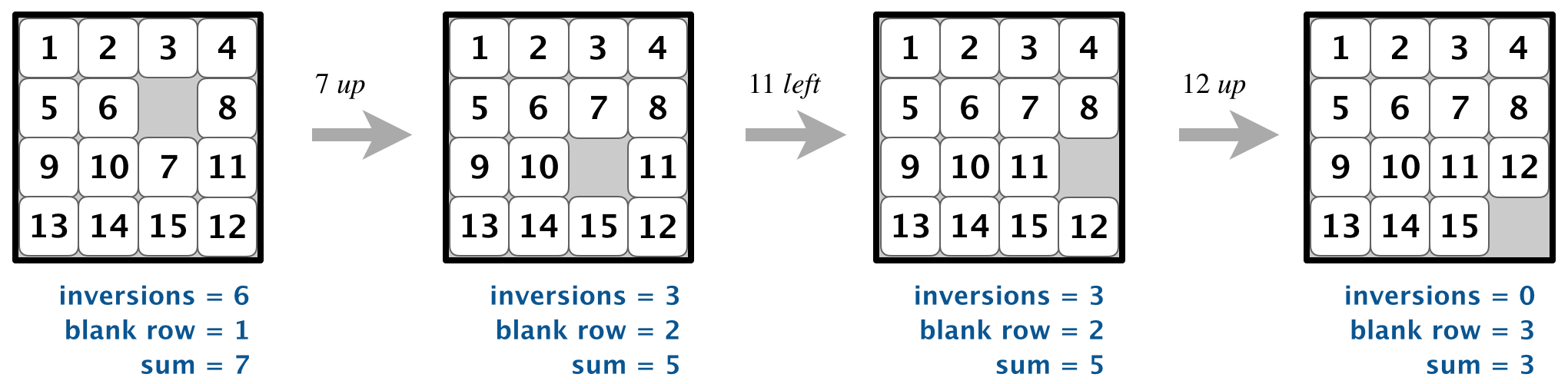
That is, when n is even, an n-by-n board is solvable if and only if the number of inversions plus the row of the blank square is odd.

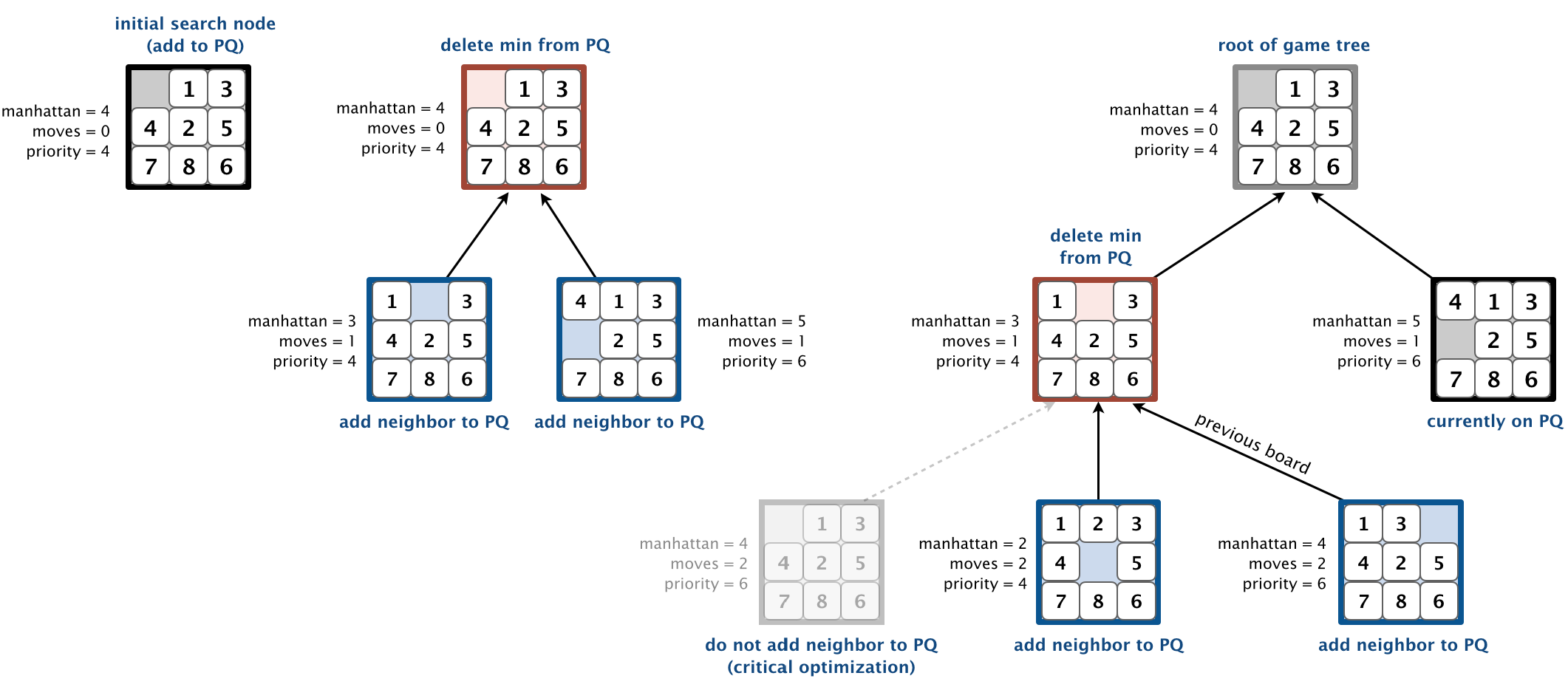
A* search. Now, we describe a solution to the 8-puzzle problem that illustrates a general artificial intelligence methodology known as the A* search algorithm. We define a search node of the game to be a board, the number of moves made to reach the board, and the previous search node. First, insert the initial search node (the initial board, 0 moves, and a null previous search node) into a priority queue. Then, delete from the priority queue the search node with the minimum priority, and insert onto the priority queue all neighboring search nodes (those that can be reached in one move from the dequeued search node). Repeat this procedure until the search node dequeued corresponds to the goal board.

The efficacy of this approach hinges on the choice of priority function for a search node. We consider two priority functions:

The Hamming priority function is the Hamming distance of a board plus the number of moves made so far to get to the search node. Intuitively, a search node with a small number of tiles in the wrong position is close to the goal, and we prefer a search node if has been reached using a small number of moves.
The Manhattan priority function is the Manhattan distance of a board plus the number of moves made so far to get to the search node.

To solve the puzzle from a given search node on the priority queue, the total number of moves we need to make (including those already made) is at least its priority, using either the Hamming or Manhattan priority function. Why? Consequently, when the goal board is dequeued, we have discovered not only a sequence of moves from the initial board to the goal board, but one that makes the fewest moves. (Challenge for the mathematically inclined: prove this fact.)

Game tree. One way to view the computation is as a game tree, where each search node is a node in the game tree and the children of a node correspond to its neighboring search nodes. The root of the game tree is the initial search node; the internal nodes have already been processed; the leaf nodes are maintained in a priority queue; at each step, the A* algorithm removes the node with the smallest priority from the priority queue and processes it (by adding its children to both the game tree and the priority queue).

For example, the following diagram illustrates the game tree after each of the first three steps of running the A* search algorithm on a 3-by-3 puzzle using the Manhattan priority function.

Solver data type. In this part, you will implement A* search to solve n-by-n slider puzzles. Create an immutable data type Solver with the following API:

public class Solver {

    // find a solution to the initial board (using the A* algorithm)
    public Solver(Board initial)

    // min number of moves to solve initial board
    public int moves()

    // sequence of boards in a shortest solution
    public Iterable<Board> solution()

    // test client (see below) 
    public static void main(String[] args)

}

Implementation requirement. To implement the A* algorithm, you must use the MinPQ data type for the priority queue.

Corner case. Throw an IllegalArgumentException in the constructor if the argument is null.

Unsolvable boards. Throw an IllegalArgumentException in the constructor if the initial board is not solvable.

Test client. Your test client should take the name of an input file as a command-line argument; print the minimum number of moves to solve the puzzle (or report that the puzzle is unsolvable); and print the sequence of boards in a corresponding solution (with each board preceded by a blank line). The input file contains the board size n, followed by the n-by-n grid of tiles, using 0 to designate the blank square.

~/Desktop/8puzzle> more puzzle04.txt 3 0 1 3 4 2 5 7 8 6 ~/Desktop/8puzzle> java-algs4 Solver puzzle04.txt Minimum number of moves = 4 3 0 1 3 4 2 5 7 8 6 3 1 0 3 4 2 5 7 8 6 3 1 2 3 4 0 5 7 8 6 3 1 2 3 4 5 0 7 8 6 3 1 2 3 4 5 6 7 8 0

~/Desktop/8puzzle> more puzzle3x3-unsolvable.txt 3 1 2 3 4 5 6 8 7 0 ~/Desktop/8puzzle> java-algs4 Solver puzzle3x3-unsolvable.txt Unsolvable puzzle

Two optimizations. To speed up your solver, implement the following two optimizations:

The critical optimization. A* search has one annoying feature: search nodes corresponding to the same board are enqueued on the priority queue many times (e.g., the bottom-left search node in the game-tree diagram above). To reduce unnecessary exploration of useless search nodes, when considering the neighbors of a search node, don’t enqueue a neighbor if its board is the same as the board of the previous search node in the game tree.
Caching the Hamming and Manhattan distances. To avoid recomputing the Hamming and Manhattan distances of a board from scratch each time during various priority-queue operations, precompute the values in the Board constructor; save them in instance variables; and return the saved values as needed. This caching technique is broadly applicable: consider using it in any situation where you are recomputing the same quantity many times and for which computing that quantity is a bottleneck operation.

Challenge for the bored. Implement a better solution which is capable of solving puzzles that the required solution is incapable of solving.

Submission. Submit the files Board.java and Solver.java (with the Manhattan priority). We will supply algs4.jar. Your may not call any library functions other than those in java.lang, java.util, and algs4.jar. You must use MinPQ for the priority queue. Finally, submit a readme.txt file and answer the questions.

Grading.

file points

Board.java 16

Solver.java 18

readme.txt 6

40

file	points
`Board.java`	16
`Solver.java`	18
`readme.txt`	6
	40

Reminder: You can lose up to 4 points for poor style and up to 4 points for inadequate unit testing.