The Atomic Nature of Matter


Download project ZIP | Submit to TigerFile

Getting Started

  • Review Section 2.4 in the textbook, especially the part on depth-first search.
  • Download and unzip atomic.zip , then open the atomic project in IntelliJ.
  • You make work with a partner on this project subject to these partnering rules.

Historical Perspective

Atoms played a central role in 20th-century physics and chemistry, but before 1908 the reality of atoms and molecules was not universally accepted. In 1827, the botanist Robert Brown observed the random, erratic motion of microscopic particles suspended in fluid. This phenomenon later became known as Brownian motion. Einstein hypothesized that the motion arises from countless collisions with much smaller particles, namely atoms and molecules.

In one of his 1905 “miracle year” papers, Einstein developed a quantitative theory of Brownian motion to help justify the existence of atoms as real, finite entities. His theory gave experimentalists a way to estimate molecular quantities using an ordinary microscope by observing the collective effect of many molecular collisions on a larger immersed particle. In 1908, Jean-Baptiste Perrin validated Einstein’s kinetic theory experimentally, providing direct evidence for the atomic nature of matter. Perrin’s experiments also yielded one of the earliest estimates of Avogadro’s number. For this work, he won the 1926 Nobel Prize in Physics.

The Problem

In this project, you will reproduce a modern version of Perrin’s experiment. Your job is greatly simplified because modern video and computer technology, combined with your programming skills, makes it possible to measure and track the motion of an immersed particle undergoing Brownian motion accurately. We provide video microscopy data of polystyrene spheres (beads) suspended in water.

The project has three pats:

  • identify beads in each frame,
  • track beads between consecutive frames to measure their displacements, and
  • analyze the displacement data by fitting Einstein’s model and estimating Avogadro’s number.

The Data

We provide 10 datasets, collected by William Ryu using fluorescent imaging. Each dataset is stored in a subdirectory named run_1 through run_10 and contains a sequence of 200 640-by-480 color images named frame00000.jpg through frame00199.jpg.

Here is a movie of several beads undergoing Brownian motion.

Below is a typical raw image (left) and a cleaned up version (right) produced by thresholding, as described below.

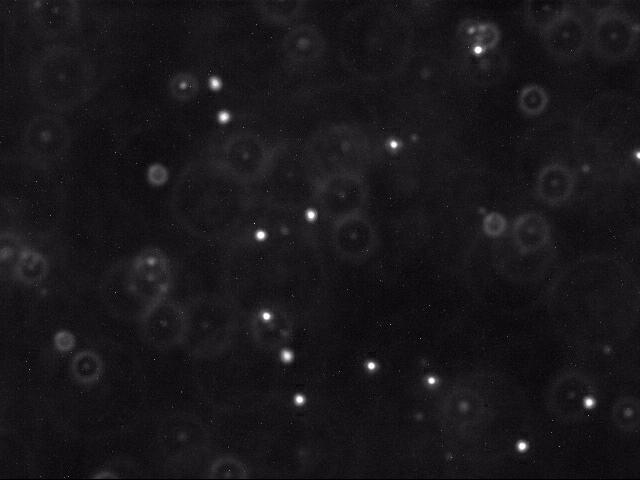frame of polystyrene spheres immersed in water
threshold frame of polystyrene spheres immersed in water

Each image shows a two-dimensional cross section of a microscope slide. The beads move within the the microscope’s field of view (the $x$- and $y$-directions). They also move in the $z$-direction, entering and leaving the microscope’s depth of focus. As a result, beads may appear with halos or disappear from the image entirely.

I. Particle Identification

Your first task is to identify beads in noisy images. Each image is 640-by-480 pixels. Each pixel is a Color object; convert it to a luminance (intensity) value between 0.0 (black) and 255.0 (white).

Whiter pixels correspond to beads (foreground) and darker pixels to water (background). The task has three steps:

  • Reading the image. Use the Picture data type to read the image.

  • Classifying the pixels as foreground or background. Use thresholding to separate foreground from background: pixels with luminance strictly below a threshold $\tau$ are background; all others are foreground. The example images above use $\tau = 180.0$. Use the intensity() method from Luminance.java.

  • Finding the beads. A bead appears as a roughly disc-shaped region of at least $min$ connected foreground pixels (typically 25). A blob (connected component) is a maximal set of connected foreground pixels, regardless of shape. We call any blob with at least $min$ pixels a bead. The center of mass of a blob is the average of the $x$- and $y$-coordinates of its pixels.

Create a helper data type Blob that has the following API.

       public class Blob {
            //  Creates an empty blob.
            public Blob()                          

            //  Adds pixel (x, y) to this blob.
            public void add(int x, int y)          

            //  Returns the number of pixels in this blob.
            public int mass()                      

            //  Euclidean distance between the centers of mass of the two blobs.
            public double distanceTo(Blob that)    

            //  Returns a string representation of this blob (see below).
            public String toString()               

            //  Tests this class by calling all instance methods directly.
            public static void main(String[] args) 
	}

Here are some details about the required behavior:

  • Coordinates. In this API, $x$ is the column index and $y$ is the row index.

  • Center of mass. The center of mass is the average of the pixels’ $x$- and $y$-coordinates.

  • String representation. The toString() method returns a string that contains, in order:

    • the blob’s mass,
    • one space,
    • the center of mass in the form $(x, y)$
    • $x$ and $y$ formatted with four digits after the decimal point.

  • Performance requirement. The constructor and each instance method must run in constant time.

Next, implement a data type BeadFinder with the following API. Use depth-first search to find connected components (blobs) in the thresholded image efficiently.

        public class BeadFinder {
            //  Finds all blobs in the given picture using luminance threshold tau.
            public BeadFinder(Picture picture, double tau)

            //  Returns all beads (blobs with >= min pixels).
            public Blob[] getBeads(int min)

            //  Test client (see below).
            public static void main(String[] args)
        }

The main() method takes three command-line arguments: an integer min, a floating-point number tau, and an image filename. It constructs a BeadFinder with threshold tau and print all beads (blobs with at least min pixels), as shown here:

~/Desktop/atomic> java-introcs BeadFinder 0 180.0 run_1/frame00001.jpg
29 (214.7241,  82.8276)
36 (223.6111, 116.6667)
 1 (254.0000, 223.0000)
42 (260.2381, 234.8571)
35 (266.0286, 315.7143)
31 (286.5806, 355.4516)
37 (299.0541, 399.1351)
35 (310.5143, 214.6000)
31 (370.9355, 365.4194)
28 (393.5000, 144.2143)
27 (431.2593, 380.4074)
36 (477.8611,  49.3889)
38 (521.7105, 445.8421)
35 (588.5714, 402.1143)
13 (638.1538, 155.0000)

~/Desktop/atomic> java-introcs BeadFinder 25 180.0 run_1/frame00001.jpg
29 (214.7241,  82.8276)
36 (223.6111, 116.6667)
42 (260.2381, 234.8571)
35 (266.0286, 315.7143)
31 (286.5806, 355.4516)
37 (299.0541, 399.1351)
35 (310.5143, 214.6000)
31 (370.9355, 365.4194)
28 (393.5000, 144.2143)
27 (431.2593, 380.4074)
36 (477.8611,  49.3889)
38 (521.7105, 445.8421)
35 (588.5714, 402.1143)

In the sample frame, there are 15 blobs, 13 of which are beads.

Q.Can I assume the image dimensions are all 640-by-480?
A.
No, your solution should handle images of any dimension.
Q.My program prints the same beads, but in a different order. Is that okay?
A.
Yes. The output order depends on how you store blobs and how you traverse the image (row-major vs. column-major).
Q.What are the conventions for pixels in a Picture?
A.
By convention, pixels are indexed by $(col, row)$. The first argument to get() is the column (increasing left-to-right) and the second is the row (increasing top-to-bottom).

II. Particle Tracking

The next step is to determine how far a bead moves time $t$ to time $t + \Delta t$. For our data, $\Delta t = 0.5$ seconds between frames. Assume each bead moves only a small amount between frames and that beads never collide. Beads may disappear between frames by leaving the field of view ($x$ or $y$) or by moving out of focus ($z$).

To track beads between consecutive frames, do the following: for each bead at time $t + \Delta t$, find the closest bead at time $t$ (Euclidean distance) and treat the pair as the same bead. If the distance exceeds $\Delta$ pixels, assume that one of the beads has either just appeared or just disappeared.

Next, write BeadTracker.java with a main() method:

  • Read min, tau, delta, and the image filenames from the command line.
  • For each pair of consecutive frames, identify beads in both images using BeadFinder.
  • Print each displacement (distance moved) that is at most delta, formatted with four digits after the decimal point, one per line, in the order discovered.
~/Desktop/atomic> java-introcs BeadTracker 25 180.0 25.0 run_1/*.jpg
7.1833
4.7932
2.1693
5.5287
5.4292
4.3962
...
Q.Do I need to track individual beads across multiple frames?
A.
No. Although tracking beads across many frames can be more accurate, this assignment only requires comparing beads in two consecutive frames.

III. Data Analysis

Einstein’s theory of Brownian motion links microscopic bead properties (such as radius and diffusivity) to macroscopic fluid properties (such as temperature and viscosity). Using video microscopy, we can estimate Avogadro’s number by observing the collective effect of many water molecules on a bead.

Estimating the self-diffusion constant $D$. The self-diffusion constant $D$ describes the random motion of a bead in water due to thermal collisions.

  • Model. In one dimension, the Einstein–Smoluchowski equation implies that a bead’s displacement over time $\Delta t$ has mean $0$ and variance $\sigma^2 = 2 D \Delta t$.
  • Estimation. Estimate $\sigma^2$ by averaging the squared displacements in the $x$- and $y$-directions.

    • Let $(\Delta x_1, \Delta y_1), \ldots, (\Delta x_n, \Delta y_n)$ be the $n$ observed displacements.

    • Let $r_1, \ldots, r_n$ denote the radial displacements.

    • $ \sigma^2 \; = \; \dfrac{(\Delta x^2_1+ \cdots + \Delta x^2_n) + (\Delta y^2_1+\cdots+\Delta y^2_n)}{2n} \; = \; \dfrac{r^2_1+\cdots+r^2_n}{2n} $

    • For our data, $\Delta t = 0.5$, so $D \approx \sigma^2$.

    • Convert pixels to meters: BeadTracker reports pixels, but the formula uses meters. To convert pixels to meters, multiply by $0.175 \times 10^{-6}$ (meters per pixel).

Estimating the Boltzmann constant $k$. The Boltzmann constant $k$ is a fundamental physical constant that relates a molecule’s average kinetic energy to its temperature. The Stokes–Einstein relation is $$D = \dfrac{k\, T}{6 \, \pi \, \eta \, \rho}.$$ It expresses the self-diffusion constant $D$ of a spherical bead in terms of $k$, the temperature $T$, the viscosity $\eta$, and the bead radius $\rho$. For our data:

  • $T = 297 \text{K}$,
  • $\eta = 9.135 \times 10^{-4} \; \text{N} \cdot \text{s} \cdot \text{m}^{-2}$, and
  • $\rho = 0.5 \times 10^{-6} \text{m}$.

Solve the Stokes–Einstein equation for $k$ using your estimate of $D$.

Estimating Avogadro’s number $N_A$. Avogadro’s number $N_A$ is the number of particles in one mole.

  • Since $k = R / N_A$, we have $N_A = R / k$, where $R \approx 8.31446 J \cdot \text{mol}^{-1} \cdot \text{K}^{-1}$ is the universal gas constant.
  • Use $R / k$ as your estimate of Avogadro’s number.

Write Avogadro.java. For the final part, write Avogadro.java with a main() method that:

  • reads the radial displacements $r_1, r_2, r_3, \ldots$ from standard input;
  • estimates Boltzmann’s constant $k$ and Avogadro’s number $N_A$ using the formulas above; and
  • prints $k$ and $N_A$ in scientific notation with four digits after the decimal point.

Here are a few sample executions. Your output should match exactly, including formatting:

~/Desktop/atomic> more displacements-run_1.txt
 7.1833
 4.7932
 2.1693
 5.5287
 5.4292
 4.3962
...

~/Desktop/atomic> java-introcs Avogadro < displacements-run_1.txt
Boltzmann = 1.2535e-23
Avogadro  = 6.6329e+23

~/Desktop/atomic> java-introcs BeadTracker 25 180.0 25.0 run_1/*.jpg | java-introcs Avogadro
Boltzmann = 1.2535e-23
Avogadro  = 6.6329e+23
Q.Do I need to worry about converting units?
A.
All parameters are given in SI units. The only conversion you need to do is from pixels to meters, as described above.
Q.My output matches the reference output, except sometimes they are off by 0.0001. Why could cause this?
A.
It is likely a combination of floating-point roundoff error and printing only 4 digits after the decimal point. For example, this discrepancy can arise if one solution computes the value 0.12345 (which gets rounded up to 0.1235) and another computes the value 0.1234499999999 (which gets rounded down to 0.1234). You need not worry about such discrepancies on this assignment.
Q.Can I use Java’s built-in libraries?
A.
You are free to use and of the libraries introduced in the course, including java.util.ArrayList.

Possible Progress Steps

Click here to show possible progress steps for Blob
  1. Observe that each directory run_1, run_2, …, run_9 contains a sequence of 200 JPEG images. In total, these data files consume 70MB of space. The file beads-run_1.txt lists the beads found in each frame of run_1 (using tau = 180.0 and min = 25). The files displacements-run_1.txt and displacements-run_2.txt are the output of BeadTracker for those runs.
  2. Implement the Blob data type. Do not store all of the individual pixels that comprise a blob; instead, store three values. Two alternatives are:
    • number of pixels, $x$-coordinate center of mass, and \(y\)-coordinate center of mass or
    • number of pixels, sum of \(x\)-coordinates, and sum of \(y\)-coordinates needed to compute the center of mass.
  3. Recall the main() method is used to write your test client. This is where you should thoroughly test your Blob implementation. For example, create various Blob objects and call the various Blob methods on these objects.
  4. Some FAQs:
  • How can I implement the toString() method to format the numbers? Use String.format(). It works like StdOut.printf(), but returns the resulting string instead of printing it. See pp. 130–132 of the textbook to learn more about formatted printing.
  • Which value should distanceTo() return if the mass of one or both blobs is zero? We recommend Double.NaN. Since this corner case is not specified in the API, we will not test it.
  • What should toString() return if the mass is zero? We recommend returning the value "0 (NaN, NaN)". Since this corner case is not specified in the API, we will not test it.
Click here to show possible progress steps for BeadFinder
  1. This is the most challenging code to implement.
  2. Review Section 2.4 in the textbook, especially the part on depth-first search. Finding all the pixels in a blob is similar to finding a percolating path.
  3. Write the constructor to find all of the blobs and initialize the instance variables. Most of the work for the BeadFinder data type will be here.
  4. The crux of this part is to write a private recursive method dfs() that locates all of the foreground pixels in the same blob as the foreground pixel (x, y). To do this, use depth-first search:
  • Mark pixel (x, y) as in the current blob.
  • Then recursively mark all of its foreground neighbors as in the current blob (but do not recur if the pixel has previously been marked or the pixel indices are out-of-bounds).
  • It is up to you to decide which arguments would be useful for the dfs() method.
  • The constructor should call dfs() from each unmarked pixel (x, y). All of the pixels encountered during a single call to dfs() comprise one blob.
  • Next, implement the method getBeads(int min) that searches through the blobs and stores all of the beads (blobs that contain at least the specified number of pixels) in a Blob array. The length of the array should be equal to the number of beads. To determine the number of beads, you may find it helpful to implement a private method countBeads(int min) that counts and returns the number of beads.
  • Implement a main() method that takes as command-line arguments min, tau, and the name of a JPEG file. The main() method prints the list of beads.
  1. Some FAQs:
  • Can I assume that the dimensions of all of the images are 640-by-480 pixels? No, do not hardwire these constants into your program. Use picture.width() and picture.height() for the width and height, respectively.
  • To compute the luminance of a pixel: First, get the Color value of that pixel. Then, use the appropriate method in Luminance.java (Program 3.1.3) to get the luminance value for that color. There is no need to copy this code.
  • Are diagonal pixels not considered adjacent? Use only the four ordinal neighbors (north, east, south, and west).
  • Must I print the beads and displacements in the same order as shown in the assignment specification? No, the order is not specified.
  1. Testing: The initial description of BeadFinder shows the output from running BeadFinder with run_1/frame00001.jpg. Note that the order in which you print the beads is not important. Here are the results for run_1/frame00000.jpg:
   java-introcs BeadFinder 0 180.0 run_1/frame00000.jpg

   37 (220.0270, 122.8919)
   1 (254.0000, 223.0000)
   17 (255.4118, 233.8824)
   23 (265.8261, 316.4348)
   36 (297.8333, 394.5000)
   39 (312.3077, 215.8205)
   23 (373.0000, 357.1739)
   19 (390.8421, 144.8421)
   31 (433.7742, 375.4839)
   32 (475.5000,  44.5000)
   31 (525.2903, 443.2903)
   24 (591.0000, 399.5000)
   35 (632.7714, 154.5714)

   java-introcs BeadFinder 25 180.0 run_1/frame00000.jpg

   37 (220.0270, 122.8919)
   36 (297.8333, 394.5000)
   39 (312.3077, 215.8205)
   31 (433.7742, 375.4839)
   32 (475.5000,  44.5000)
   31 (525.2903, 443.2903)
   35 (632.7714, 154.5714)

java-introcs BeadFinder 0 180.0 run_6/frame00010.jpg

    1 ( 25.0000, 373.0000)
    1 ( 26.0000, 372.0000)
    1 ( 27.0000, 373.0000)
    1 ( 29.0000, 369.0000)
   63 ( 34.2063,  32.3175)
    9 ( 97.0000, 341.0000)
   65 (141.4615,  54.0615)
   70 (165.8571, 165.2857)
   60 (173.5667, 200.5333)
   50 (198.7000, 113.0200)
    1 (254.0000, 223.0000)
   89 (276.9101, 306.6629)
   24 (296.3750,  82.9583)
   62 (306.6774, 474.6774)
   59 (339.1356,  81.5932)
   68 (358.9706, 159.0588)
   40 (397.0750,  39.2000)
   86 (573.3488, 427.0581)
   51 (611.7451, 143.8235)
   53 (636.1132, 230.6038)
   14 (634.5000, 421.7143)
   26 (636.5000,  35.0000)

   java-introcs BeadFinder 25 180.0 run_6/frame00010.jpg

   63 ( 34.2063,  32.3175)
   65 (141.4615,  54.0615)
   70 (165.8571, 165.2857)
   60 (173.5667, 200.5333)
   50 (198.7000, 113.0200)
   89 (276.9101, 306.6629)
   62 (306.6774, 474.6774)
   59 (339.1356,  81.5932)
   68 (358.9706, 159.0588)
   40 (397.0750,  39.2000)
   86 (573.3488, 427.0581)
   51 (611.7451, 143.8235)
   53 (636.1132, 230.6038)
   26 (636.5000,  35.0000)
Click here to show possible progress steps for BeadTracker
  1. The main() method in BeadTracker takes an arbitrary number of command-line arguments, args[0], args[1], and so forth.
  2. You need to consider only two frames at a time, so do not store all of the frames at the same time.
  3. Use the Picture data type to read a JPEG file.
  4. Some FAQs
  • What should I do if several of the beads in frame t+1 have the same bead in frame t as their closest bead? That happens only rarely, so you should not worry about it—just let the bead in frame t get paired a second time.
  • I am able to find beads and blobs correctly, but my BeadTracker gives a few errors, despite that it is mostly working. Why could this be?
    • Check that, for each bead in frame t + 1, you are finding the closest bead in frame t, and not vice versa.
    • Be sure to discard distances greater than delta, not greater than or equal to delta.
  • Why do I have to compare each bead in frame t + 1 to each bead in frame t? Why can’t I do it the other way around? It is an arbitrary choice, but one that you must follow because it is prescribed in the assignment specification.
  • Can I assume that all of the runs consist of 200 frames? No, do not hardwire 200 into your program. Use args.length for the number of command-line arguments.
  • How can I specify 200 image names on the command line? Use the wildcard capability of the terminal. For example, the following specifies (in alphabetical order) all .jpg files in the run_1 directory.
   java-introcs BeadTracker 25 180.0 25.0 run_1/*.jpg
  1. Testing: For reference, displacements-run_1.txt, displacements-run_2.txt, and displacements-run_6.txt contain a list of all of the displacements (using tau = 180.0 and min = 25) for run_1, run_2, and run_6, respectively. They were obtained by running
   java-introcs BeadTracker 25 180.0 25.0 run_1/*.jpg

   7.1833
   4.7932
   2.1693
   5.5287
   5.4292
   4.3962
   ...

   java-introcs BeadTracker 25 180.0 25.0 run_2/*.jpg

   5.1818
   7.6884
   6.7860
   6.4907
   4.2102
   1.1412
   4.4724
   7.5191
   3.0659
   4.4238
   5.0600
   1.7280
   ...

   java-introcs BeadTracker 25 180.0 25.0 run_6/*.jpg

   11.1876
   12.4269
   10.3113
    1.3954
    3.3196
    0.4732
    1.7367
    3.0060
    4.6087
    1.3282
    ...
Click here to show possible progress steps for Avogadro
  1. The main() method in Avogadro reads a sequence of floating-point numbers from standard input and prints the estimate of Avogadro’s number using the formulas provided in the assignment.
  2. To calculate \(σ^2\), use the second formula listed with radial displacements; these are the results from BeadTracker.
  3. Some FAQs:
  • How accurate of an estimate should I get? You should get within 10% or so of the exact value for Avogadro’s number \(6.022142 × 10^{23}\). The standard deviation of the radius of the beads is about 10%, so you should not expect results more accurate than this. Your output, however, should agree exactly with ours.
  • My physics is a bit rusty. Do I need to worry about converting units? Not much, since all of the constants are in SI units. The only conversion you should need to do is to convert from distances measured in pixels (the radial displacements) to distances measured in meters, by using the conversion factor of \(0.175 × 10^{−6}\) meters per pixel.
  • Checkstyle complains about the variables I named T and R. Which names should I use instead? A constant variable (a variable whose value does not change during the execution of a program, or from one execution of the program to the next) should begin with an uppercase letter and use underscores to separate any word boundaries, such as GRAVITATIONAL_CONSTANT. Constant variables should have more meaningful names, such as TEMPERATURE or GAS_CONSTANT.
  1. Testing - below are the output for displacements-run_1.txt, displacements-run_2.txt, and displacements-run_6.txt.
java-introcs Avogadro < displacements-run_1.txt

Boltzmann = 1.2535e-23
Avogadro  = 6.6329e+23

java-introcs Avogadro < displacements-run_2.txt

Boltzmann = 1.4200e-23
Avogadro  = 5.8551e+23

java-introcs Avogadro < displacements-run_6.txt

Boltzmann = 1.3482e-23
Avogadro  = 6.1670e+23
Click here to show possible progress steps for system testing
  1. As a final test, combine the data collection (BeadTracker) for run_1, run_2, and run_6 with the data analysis (Avogadro). The data for run_2 contains light boundary pixels and run_6 contains pixels whose luminance is exactly 180.0.
   java-introcs BeadTracker 25 180.0 25.0 run_1/*.jpg | java-introcs Avogadro

   Boltzmann = 1.2535e-23
   Avogadro  = 6.6329e+23

   java-introcs BeadTracker 25 180.0 25.0 run_2/*.jpg | java-introcs Avogadro

   Boltzmann = 1.4200e-23
   Avogadro  = 5.8551e+23

java-introcs BeadTracker 25 180.0 25.0 run_6/*.jpg | java-introcs Avogadro

   Boltzmann = 1.3482e-23
   Avogadro  = 6.1670e+23

Performance Analysis

Formulate a hypothesis for the running time (in seconds) of BeadTracker as a function of the input size $n$, where $n$ is the total number of pixels read across all processed frames. Use a power-law model: $$ T(n) = a \, n^b.$$

  • Use the doubling hypothesis and justify your results with empirical data. Provide data from at least three experiments.

  • Report only numeric values for $a$ and $b$.

Answer all questions in readme.txt.

Q.How can I estimate the running time of BeadTracker?
A.
Use the Stopwatch data type from Section 4.1. Remember to remove it and any additional print statements from your submitted version of BeadTracker.java. When you execute BeadTracker, redirect the output to a file to avoid measuring the time to print the output to the terminal. Run BeadTracker with a variety of input sizes which allow you to get good timing data and form a doubling hypothesis.
Q.How can I run BeadTracker with a variety of input sizes?
A.

All of the runs have 200 frames. However, when you are performing timing experiments, you can simply use a subset of them. Use use the wildcard capability of the terminal to run 10 frames, 20 frames, 40 frames, 80 frames, and 160 frames, as follows:

~/Desktop/atomic> java-introcs -Xint BeadTracker 25 180.0 25.0 run_1/frame000[0]*.jpg    > temp.txt

~/Desktop/atomic> java-introcs -Xint BeadTracker 25 180.0 25.0 run_1/frame000[0-1]*.jpg  > temp.txt

~/Desktop/atomic> java-introcs -Xint BeadTracker 25 180.0 25.0 run_1/frame000[0-3]*.jpg  > temp.txt

~/Desktop/atomic> java-introcs -Xint BeadTracker 25 180.0 25.0 run_1/frame000[0-7]*.jpg  > temp.txt

~/Desktop/atomic> java-introcs -Xint BeadTracker 25 180.0 25.0 run_1/frame000*.jpg run_1/frame001[0-5]*.jpg > temp.txt
Q.Do I need to use the -Xint option?
A.
You can try your experiments with or without the -Xint option. Recall, that -Xint turns off Java optimization, so you may get clearer results when you use the doubling method.
Q.How long should BeadTracker take?
A.
It depends on the speed of your computer, but processing 200 frames should take about 10 seconds or less without the -Xint option and about two minutes with the -Xint option.
Q.How much memory should my program use?
A.

The reference solution uses less than 10 MB. You will receive a deduction if you use substantially more. The most common way to waste memory is to hold references to an array of Picture objects in BeadTracker instead of only two at a time. You can use the -Xmx option to limit how much memory Java uses: for example, the following command limits the memory available to Java to 10 MB.

   java-introcs -Xint -Xmx10m BeadTracker 25 180.0 25.0 run_1/*.jpg
Q.When I test with a very small luminance threshold, I get a StackOverflowError, but my code works for larger luminance thresholds. What does this mean?
A.

Since DFS is recursive, it consumes memory proportional to the height of the function-call tree. If the luminance threshold is small, the blobs can be very big, and the height of the function-call tree may be very large. We will not test your program on inputs with such big blobs. If, however, you are determined to get it to work on such cases, use the command-line option -Xss20m to increase the stack space.

   java-introcs -Xint -Xss20m BeadTracker 25 18.0 25.0 run_1/*.jpg

Submission.

Upload all required files to TigerFile :

  • Blob.java
  • BeadFinder.java
  • BeadTracker.java
  • Avogadro.java
  • readme.txt
  • acknowledgments.txt

Do not submit stdlib.jar, Luminance.java, Stack.java, Queue.java, or ST.java.

Grading Breakdown

Files Points
Style 10
Blob.java 14
BeadFinder.java 32
BeadTracker.java 22
Avogadro.java 14
Analysis and readme.txt 8
Total 100

Enrichment.

What is polystyrene? It is an inexpensive plastic that is used in many everyday things including plastic forks, drinking cups, and the case of your desktop computer. Styrofoam is a popular brand of polystyrene foam. Computational biologists use micron size polystyrene beads (also known as microspheres and latex beads) to capture a single DNA molecule, e.g., for a DNA test.

What is the history of measuring Avogadro’s number? In 1811, Avogadro hypothesized that the number of molecules in a liter of gas at a given temperature and pressure is the same for all gases. Unfortunately, he was never able to determine this number that would later be named after him. Johann Josef Loschmidt, an Austrian physicist, gave the first estimate for this number using the kinetic gas theory. In 1873 Maxwell estimated the number of be around \(4.3 × 10^{23}\); later Kelvin estimated it to be around \(5 × 10^{23}\). Perrin gave the first “accurate” estimate (\(6.5–6.8 × 10^{23}\)) of, what he coined, Avogadro’s number. The most accurate estimates for Avogadro’s number and Boltzmann’s constant are computed using x-ray crystallography: Avogadro’s number is approximately \(6.022142 × 10^{23}\); Boltzmann’s constant is approximately \(1.3806503 × 10^{−23}\).

Where can I learn more about Brownian motion? Here’s the Wikipedia entry. You can learn about the theory in ORF 309. It may be the first subject you will be asked about if you interview on Wall Street.

This assignment was created by David Botstein, Tamara Broderick, Ed Davisson, Daniel Marlow, William Ryu, and Kevin Wayne.

Copyright © 2005-2026, Kevin Wayne