4. Recursion
Download project ZIP
| Submit to TigerFile
In this assignment, you will compute Delannoy numbers using recursion and dynamic programming. You will plot a Sierpinski triangle using recursion, then create an original recursive pattern of your own design.
Getting Started
- Read Sections 2.3 and 4.1 of the textbook and review the corresponding lectures and precepts.
- Review the StdDraw API.
- Download and unzip recursion.zip
, then open the
recursionproject in IntelliJ.
Delannoy Numbers (brute force)
Write a program DelannoyBrute.java that takes two integer command-line arguments $m$ and $n$
and prints the Delannoy number $D(m, n)$.
The Delannoy number $D(m, n)$ is the number of paths from $(0,0)$ to $(m, n)$ in an $m$-by-$n$ grid
using only single steps north, east, and northeast.
For example, $D(2, 2) = 13$ because these are $13$ Delannoy paths in a 2-by-2 grid:
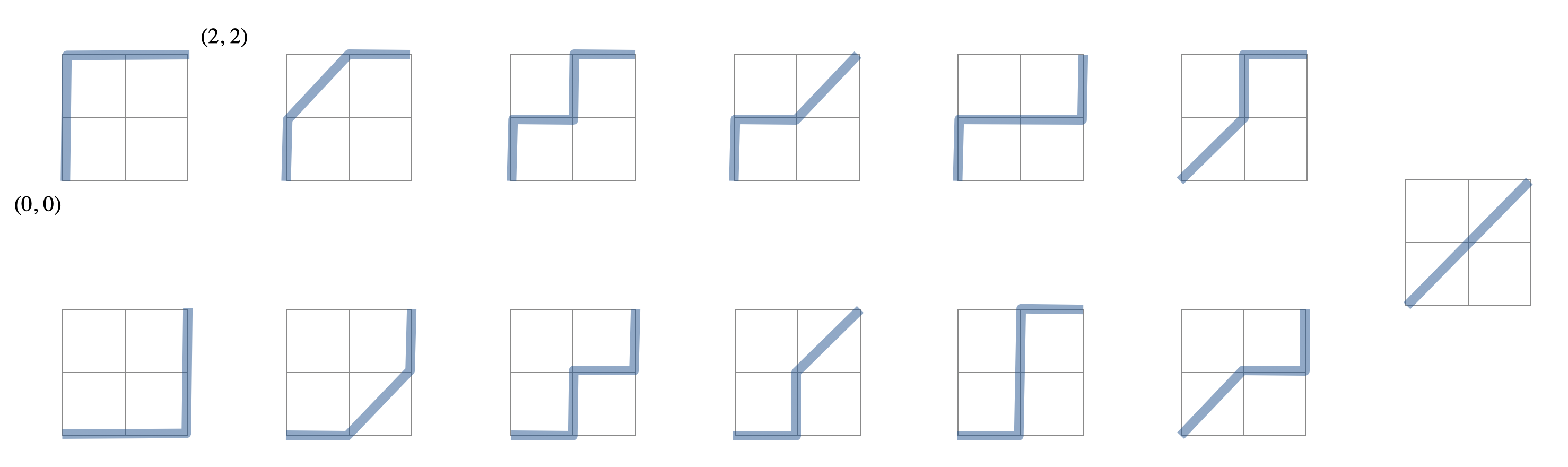
Use the following recurrence to compute $D(m,n)$:
$$
\displaystyle D(m, n) \; = \;
\begin{cases}
\;\; 1 & \text{if } m = 0 \\[.5em]
\;\; 1 & \text{if } n = 0 \\[.5em]
\;\; D(m-1, n) + D(m-1, n-1) + D(m, n-1) & \text{otherwise}
\end{cases}
$$
Organize your program according to the following public API:
public class DelannoyBrute {
// Returns the Delannoy number D(m, n).
public static long count(int m, int n)
// Takes two integer command-line arguments m and n and prints D(m, n).
public static void main(String[] args)
}
This brute-force approach is far too slow, even for moderately small $m$ and $n$.
~/Desktop/recursion> java-introcs DelannoyBrute 2 2 13 ~/Desktop/recursion> java-introcs DelannoyBrute 3 2 25 ~/Desktop/recursion> java-introcs DelannoyBrute 2 3 25 ~/Desktop/recursion> java-introcs DelannoyBrute 3 3 63 ~/Desktop/recursion> java-introcs DelannoyBrute 20 20 [takes too long]
Q.Can I assume $m \ge 0$ and $n \ge 0$?
Context: Delannoy numbers arise in combinatorics and computational biology. For example, $D(m,n)$ is the number of global alignments of two strings of lengths $m$ and $n$.
Delannoy Numbers (dynamic programming)
Now, write a program DelannoyMemo.java that takes two integer command-line arguments $m$ and $n$
and computes the Delannoy number $D(m, n)$ using dynamic programming (memoization).
Model your solution after FibonacciMemo.java (lecture) and PalindromeMemo.java (precept).
Use a private static two-dimensional array memo[][] such that memo[i][j] stores $D(i, j)$.
Organize your program according to the following API:
public class DelannoyMemo {
// Returns the Delannoy number D(m, n).
public static long count(int m, int n)
// Takes two integer command-line arguments m and n and prints D(m, n).
public static void main(String[] args)
}
Below are some sample executions. Unlike the brute-force version, the memoization version is fast enough to handle much larger values of $m$ and $n$.
~/Desktop/recursion> java-introcs DelannoyMemo 2 2 13 ~/Desktop/recursion> java-introcs DelannoyMemo 3 2 25 ~/Desktop/recursion> java-introcs DelannoyMemo 2 3 25 ~/Desktop/recursion> java-introcs DelannoyMemo 3 3 63 ~/Desktop/recursion> java-introcs DelannoyMemo 20 20 260543813797441
Analysis
Conduct the following computational experiments and measure the running time:
~/Desktop/recursion> java-introcs DelannoyBrute 2 2 ~/Desktop/recursion> java-introcs DelannoyBrute 4 4 ~/Desktop/recursion> java-introcs DelannoyBrute 8 8 ~/Desktop/recursion> java-introcs DelannoyBrute 16 16 ~/Desktop/recursion> java-introcs DelannoyMemo 2 2 ~/Desktop/recursion> java-introcs DelannoyMemo 4 4 ~/Desktop/recursion> java-introcs DelannoyMemo 8 8 ~/Desktop/recursion> java-introcs DelannoyMemo 16 16 ~/Desktop/recursion> java-introcs -Xss10m DelannoyMemo 3000 3000 ~/Desktop/recursion> java-introcs -Xss10m DelannoyMemo 6000 6000 ~/Desktop/recursion> java-introcs -Xss10m DelannoyMemo 12000 12000 ~/Desktop/recursion> java-introcs -Xss10m DelannoyMemo 24000 24000
Based on the results, answer the following questions in readme.txt:
- Which runs faster:
DelannoyBrute.count()orDelannoyMemo.count()? - Estimate the order of growth of the running time of
DelannoyBrute.count(n, n)as a function of $n$? - Estimate the order of growth of the running time of
DelannoyMemo.count(n, n)as a function of $n$.
Q.What does the command-line option -Xss10m do?
Q.I’m getting a java.lang.OutOfMemoryError?
Try allocating more heap memory with -Xmx.
The heap is used for arrays and other objects.
`java-introcs -Xss50m -Xmx5g DelannoyMemo 24000 24000
Q.Should I worry if count() overflows a long?
count() since it does not impact the running time.Q.How should I measure the running time of count()?
System.currentTimeMillis().
But be sure to remove this code before submitting.Sierpinski Triangle
The Sierpinski triangle is a classic fractal pattern, like the H-tree from Section 2.3 of the textbook.






Despite its complexity, the Sierpinski triangle can be generated with a short recursive function.
Your primary task is to write sierpinski(), which that draws a Sierpinski
triangle of order $n$ at a specified location and size.
I should draw one filled, downward-pointing equilateral triangle,
then call itself three times (with an appropriate base case).
In main(), read n from the command line and draw the outline triangle.
Then call sierpinski() to draw the Sierpinski triangle of order n inside the outline.
Organize your program into four functions, as specified in the following API:
public class Sierpinski {
// Height of an equilateral triangle with the given side length.
public static double height(double length)
// Draws a filled equilateral triangle with the given side length
// whose bottom vertex is at (x, y).
public static void filledTriangle(double x, double y, double length)
// Draws a Sierpinski triangle of order n in which the largest filled
// triangle has the given side length and bottom vertex at (x, y).
public static void sierpinski(int n, double x, double y, double length)
// Takes an integer command-line argument n; draws the outline of an
// upward-pointing equilateral triangle of side length 1 with vertices
// (0, 0), (1, 0), and (1/2, sqrt(3) / 2); and draws a Sierpinski
// triangle of order n that fits inside the outline.
public static void main(String[] args)
}
Geometry
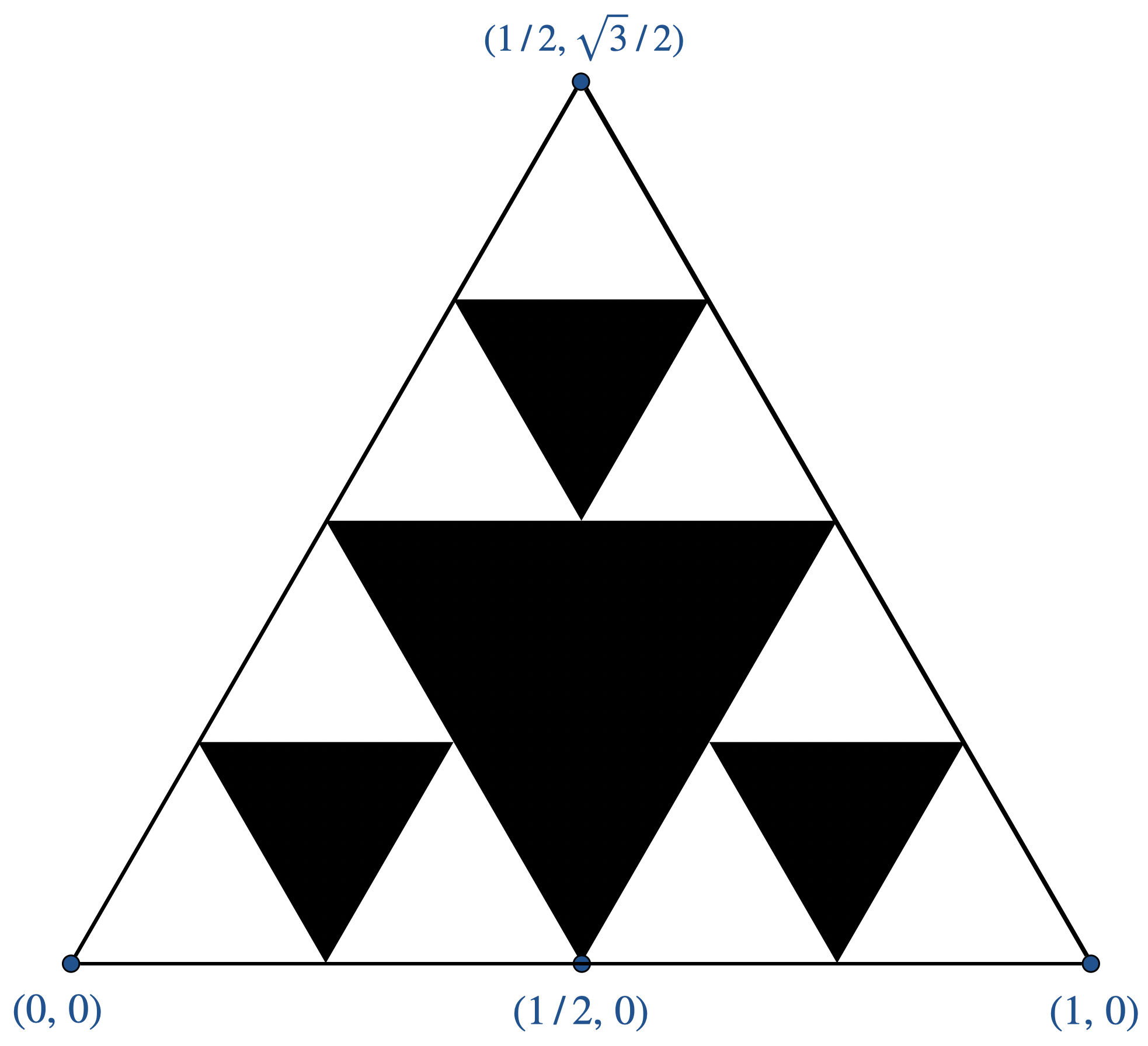
The diagram below shows the outline triangle and an order-2 Sierpinski triangle inside it.
- The outline triangle has vertices $(0, 0)$, $(1, 0)$, and $( 1 / 2, \sqrt{3} / 2)$.
- The order-2 Sierpinski triangle has side length $1 / 2$ and bottom vertex is $(1 / 2 , 0)$.
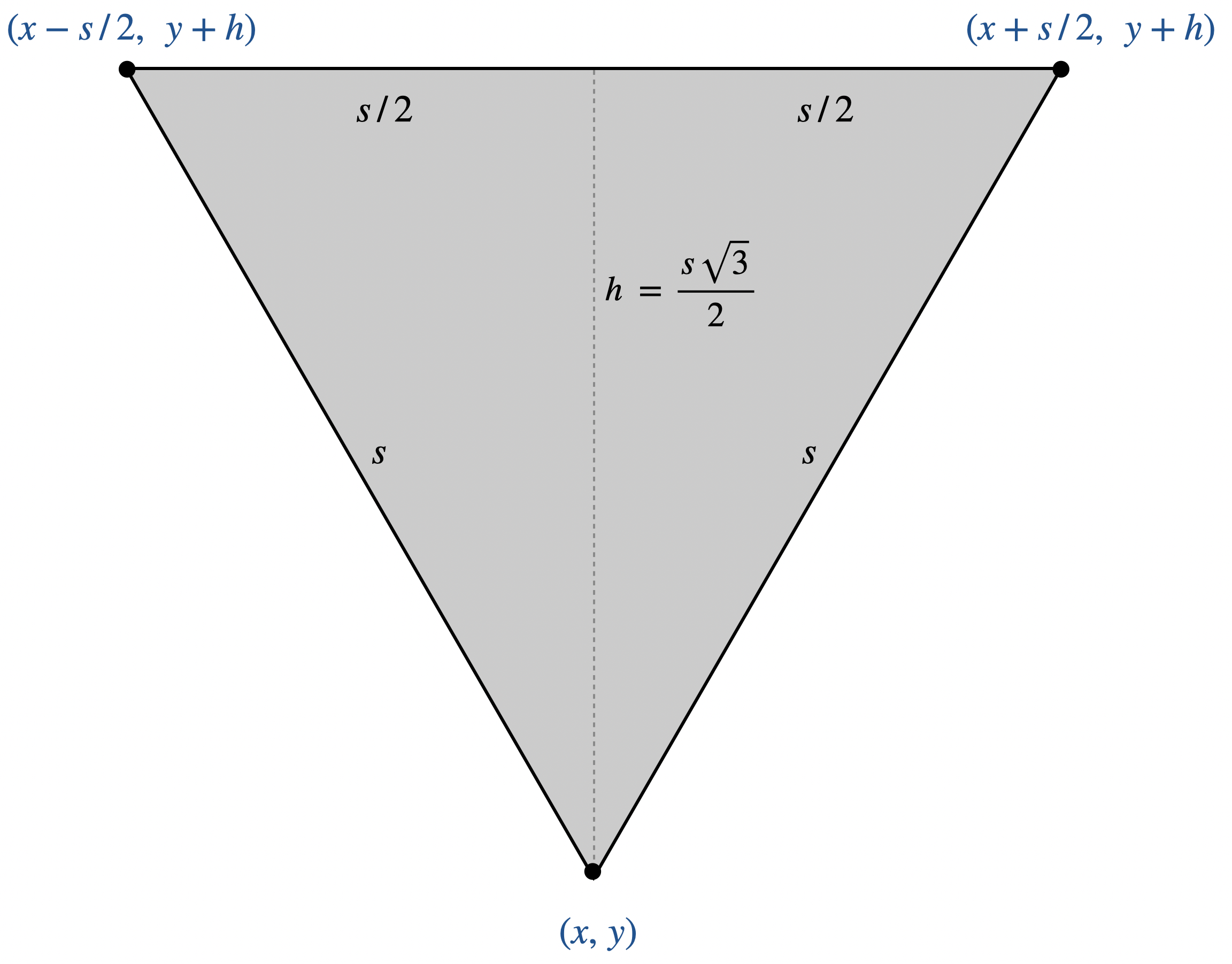
The diagram below shows a downward-pointing equilateral triangle of side length $s$ whose bottom vertex is $(x, y)$.
- The height is $h = s \sqrt{3} \; / \; 2$.
- The vertices are $(x, y)$, $(x - s/2, y + h)$, and $(x + s/2, y + h)$.
Requirements
When implementing Sierpinski.java, follow these requirements:
- Draw filled triangles using
StdDraw.filledPolygon(). - Draw the outline triangle using
StdDraw.polygon(). - Do not call any method in
StdDrawbesidespolygon()andfilledPolygon(). These restrictions ensure consistent grading output. - Do not add any public methods. You may add private helper methods.
Here are some sample executions. Your output should match exactly.
~/Desktop/recursion> java-introcs Sierpinski 1~/Desktop/recursion> java-introcs Sierpinski 2
~/Desktop/recursion> java-introcs Sierpinski 3

Q.I’m stuck. Can you suggest some steps for making steady, incremental progress?
These steps are optional. Use them as needed.
-
Review Htree.java from the textbook, lecture, and precept.
-
Create
Sierpinski.java. Copy the provided API into the file, then make the minimal changes needed for it to compile. -
Write the function
height(). The body of this method should be a one-liner (no recursion). -
Test: In
main(), callheight()a few times with different arguments and verify the results. -
In
main(), draw the outline of the initial equilateral triangle. Useheight()to compute the top vertex. -
Write
filledTriangle(x, y, length). Again, no recursion. -
Test: In
main(), callfilledTriangle()a few times with different arguments and verify the results.
Now implement the recursive function sierpinski(). Use an incremental approach:
-
Write a recursive function
sierpinski()that takes one argumentn, prints the valuen, and then calls itself three times with the valuen-1. The recursion should stop whennbecomes 0. -
Test: in
main(), readnfrom the command line and callsierpinski(n). Ignoring whitespace, your output should match the output below. Make sure you understand why the values are printed in that order.~/Desktop/recursion> java-introcs Sierpinski 0 [no output] ~/Desktop/recursion> java-introcs Sierpinski 1 1 ~/Desktop/recursion> java-introcs Sierpinski 2 2 1 1 1 ~/Desktop/recursion> java-introcs Sierpinski 3 3 2 1 1 1 2 1 1 1 2 1 1 1 ~/Desktop/recursion> java-introcs Sierpinski 4 4 3 2 1 1 1 2 1 1 1 2 1 1 1 3 2 1 1 1 2 1 1 1 2 1 1 1 3 2 1 1 1 2 1 1 1 2 1 1 1
-
Modify
sierpinski()so that it prints bothnand the triangle side length. The method should now take two arguments:nandlength. -
In
main(), callsierpinski(n, 0.5), since the largest filled triangle has side length 0.5. -
At each recursive level, halve
length. -
Test: Ignoring whitespace, your program should produce the output below:
~/Desktop/recursion> java-introcs Sierpinski 0 [no output] ~/Desktop/recursion> java-introcs Sierpinski 1 1 0.5 ~/Desktop/recursion> java-introcs Sierpinski 2 2 0.5 1 0.25 1 0.25 1 0.25 ~/Desktop/recursion> java-introcs Sierpinski 3 3 0.5 2 0.25 1 0.125 1 0.125 1 0.125 2 0.25 1 0.125 1 0.125 1 0.125 2 0.25 1 0.125 1 0.125 1 0.125 ~/Desktop/recursion> java-introcs Sierpinski 4 4 0.5 3 0.25 2 0.125 1 0.0625 1 0.0625 1 0.0625 2 0.125 1 0.0625 1 0.0625 1 0.0625 2 0.125 1 0.0625 1 0.0625 1 0.0625 3 0.25 2 0.125 1 0.0625 1 0.0625 1 0.0625 2 0.125 1 0.0625 1 0.0625 1 0.0625 2 0.125 1 0.0625 1 0.0625 1 0.0625 3 0.25 2 0.125 1 0.0625 1 0.0625 1 0.0625 2 0.125 1 0.0625 1 0.0625 1 0.0625 2 0.125 1 0.0625 1 0.0625 1 0.0625
-
Modify
sierpinski()so that it takes four arguments:n,x,y, andlength. The method should draw a Sierpinski triangle of ordernwith side lengthlengthand bottom vertex $(x, y)$. This is one of the more challenging steps, so sketch a few levels on paper first. Which arguments change between the three recursive calls? -
Test: Your program should draw the Sierpinski triangles that match the sample executions above the Possible Progress Steps.
-
Remove all print statements before submitting to TigerFile.
Context: The Polish mathematician Wacław Sierpiński described this pattern in 1915, but similar motifs appear in Italian art dating back to the 13th century.
Create Your Recursive Art
In this part, you will writeArt.java, a program that produces a recursive drawing of your own design.
This part is meant to be fun, but the guidelines below may help if you are not sure where to start.
A good approach is to choose a self-referential pattern as your target output. For inspiration, see this Wikipedia list of fractals. Some patterns are harder to generate than others, and some require trigonometry.
Design your drawing before you code it. Sketch your idea on paper and plan your approach. As usual, comment your code as you go.
Requirements
-
Art.javamust take one integer command-line argumentnthat controls the recursion depth. -
Your drawing must stay within the drawing window for all
nbetween 1 and 6 (inclusive). The autograder will not test values ofnoutside this range. -
You may not change the canvas size. You may change the scale.
-
Do not play sound.
-
Your drawing may be a geometric pattern, a randomized construction, or anything else that takes advantage of recursion.
-
Optional: You may use the
Transform2Dlibrary from precept. You may also define additional transforms inArt.java(e.g., shear, reflection across the $x$- or $y$-axis, or rotation about an arbitrary point). You may copyTransform2D.javainto your local project for reference, but do not submit it. We will use the Ed Lessons implementation when grading. -
Organize your program into at three functions, including
main(). All functions exceptmain()must beprivate. -
Your artwork must genuinely rely on recursion and must be substantially different from the in-class examples (
HTree,Sierpinski,NestedCircles). -
To earn full credit, do at least two of the following:
- Use mutually recursive methods.
- Use multiple recursive methods.
- Use recursion that does not always recurse from level
nto leveln-1. - Draw between recursive calls, not only before or after all recursive calls.
- Use the recursion level for a secondary purpose (e.g., to control the color).
- Call one or more
Transform2Dmethods (or implement additional transforms) - Use different
StdDrawprimitives than the examples (e.g., ellipses, arcs, or text). - Use a non-constant number of recursive calls per level (e.g., conditional recursion).
- Use additional parameters that affect the recursion or drawing, such as an angle, aspect ratio, color/opacity, branching factor, or a random seed.
-
You may use GIF, JPG, or PNG files in your artwork. If you do, submit them with your other files. In
readme.txt, clearly indicate which parts of the design are yours and which parts come from the image files.
Q.What will cause me to lose points on the artistic part?
See the rubric in the bulleted list above. In particular, you may lose points for either of the following:
- Recursion is not essential. You will lose points if the same artwork can be created just as easily without recursion (for example, with a simple loop). As a rule of thumb, if your recursive call tree is essentially straight line (one recursive call per level), it is probably too simple.
- Too similar to in-class examples. Even if the picture looks different,
you will lose points if the code and recursion structure are essentially the
same as
HTree,Sierpinski, orNestedCircles. For example, the Quadricross looks different, but the code to generate it is very similar toHTree.
Student Art
Here is an animation we produced using student art:
Submission
Upload all files to TigerFile :
DelannoyBrute.javaDelannoyMemo.javaSierpinski.javaArt.java(and optional image files)readme.txt-acknowledgments.txt
Note: We may anonymously publish your art. If you object, please indicate so in your readme.txt when asked. We also reserve the right to pull any art, at any time, for whatever reason; by submitting your assignment, you implicitly agree with this policy.
Grading Breakdown
| File | Points |
|---|---|
| DelannoyBrute.java | 6 |
| DelannoyMemo.java | 6 |
| Sierpinski.java | 16 |
| Art.java | 6 |
| readme.txt | 6 |
| Total | 40 |