5. Object Oriented Programming
Download project ZIP
| Submit to TigerFile
In this assignment, you will write programs that use and create data types.
You will use Picture and Color to process images and In to read input from files.
Getting Started
- Read Sections 3.1 and 3.2 of the textbook and review the corresponding lectures and precepts.
- Download and unzip oop.zip
, then open the
oopproject in IntelliJ. - Consult the Picture, Color, and In APIs as needed.
Partnering
This is a partner assignment. Partnering is optional, but we strongly recommend doing at least one partnered assignment. Pair programming improves how you communicate about code and is often faster, less error-prone, and less frustrating than working alone.
- See Ed for instructions on finding a parter and creating a TigerFile group.
- Follow these partnering rules.
Rectangular Tile of an Image
A rectangular tile repeats an image in a grid with a specified number of columns and rows. For example, consider the following image:

Here is a 6-by-3 rectangular tile:

Write a program Tile.java that takes three command-line arguments
(the image filename, the number of columns, and the number of rows)
and displays the corresponding rectangular tile.
Organize your program according to the following API:
public class Tile {
// Returns a cols-by-rows tiling of the given image.
public static Picture tile(Picture picture, int cols, int rows)
// Takes three command-line arguments (the image filename, the number
// of columns, and the number of rows), and displays a rectangular
// tiling of the image with the given number of columns and rows.
public static void main(String[] args)
}
Here are some sample executions:
~/Desktop/oop> java-introcs Tile heart.png 1 1~/Desktop/oop> java-introcs Tile heart.png 6 3
~/Desktop/oop> java-introcs Tile princeton.png 1 1
~/Desktop/oop> java-introcs Tile princeton.png 5 2
~/Desktop/oop> java-introcs Tile bricks.png 1 1
~/Desktop/oop> java-introcs Tile bricks.png 9 4

Tracker
In this part, you will create a data type for a tracking device, such as an AirTag or Tile Pro. Each tracking device has a name and a location. A device may also be in lost mode, which conserves power and limits access to personal information.
Implement Tracker.java as specified by the following API:
public class Tracker {
// Creates a tracker with the given name and initial location.
// Lost mode is initially disabled.
public Tracker(String name, double initialLatitude, double initialLongitude)
// Is this tracker in lost mode?
public boolean isInLostMode()
// Enables lost mode on this tracker.
public void enableLostMode()
// Disables lost mode on this tracker.
public void disableLostMode()
// Moves this tracker to the given location.
public void move(double newLatitude, double newLongitude)
// Returns the great-circle distance between the two trackers.
public double distanceTo(Tracker other)
// Returns a string representation of this tracker.
public String toString()
// Unit tests the Tracker data type.
public static void main(String[] args)
}
Here is some more information about the required behavior:
-
Test client. The
main()method must call every public instance method. -
String representation. Return a string consisting of the tracker name and its current location (latitude, longitude) in the following format:
"backpack (40.34386, -74.6593)" -
Corner cases. You may assume that all arguments are meaningful values (e.g., not
null,NaN,Double.POSITIVE_INFINITY, orDouble.NEGATIVE_INFINITY). -
Locations. Locations are specified using latitude and longitude in degrees. For example, Nassau Hall is located at $40.34386^\circ$ latitude and $-74.6593^\circ$ longitude.
-
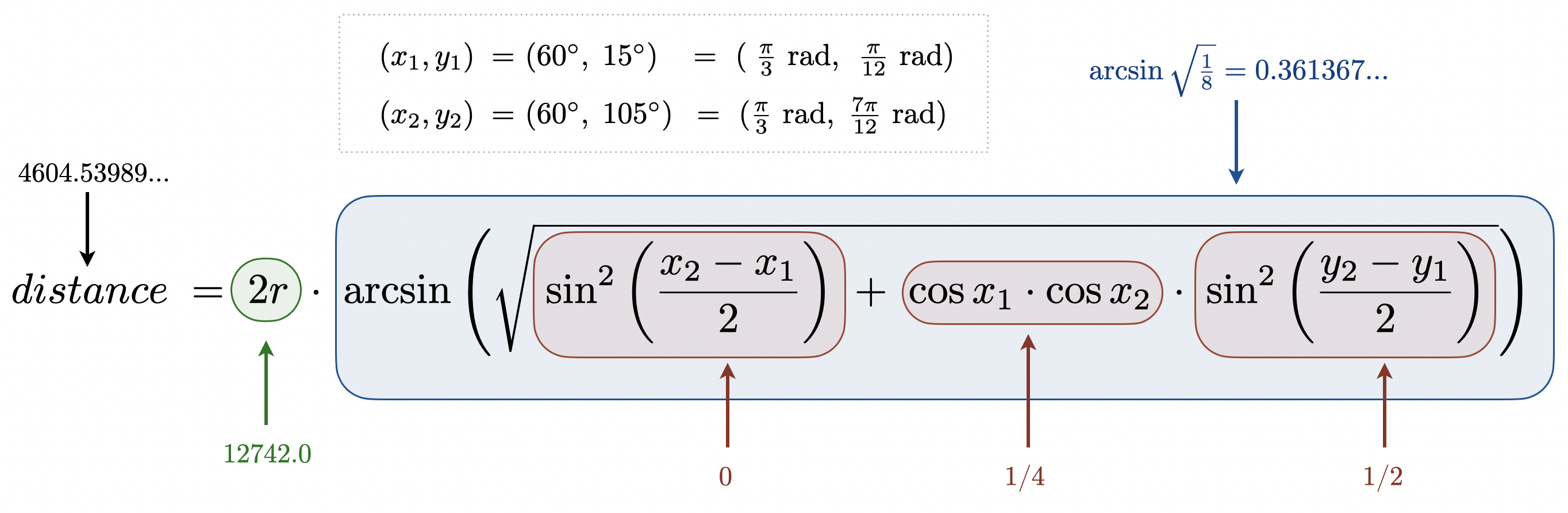
Distance. Let $(x_1, y_1)$ and $(x_2, y_2)$ be the latitude and longitude of two points on the surface of a sphere of radius $r$. The great-circle distance between them is the length of the shortest path along the surface.
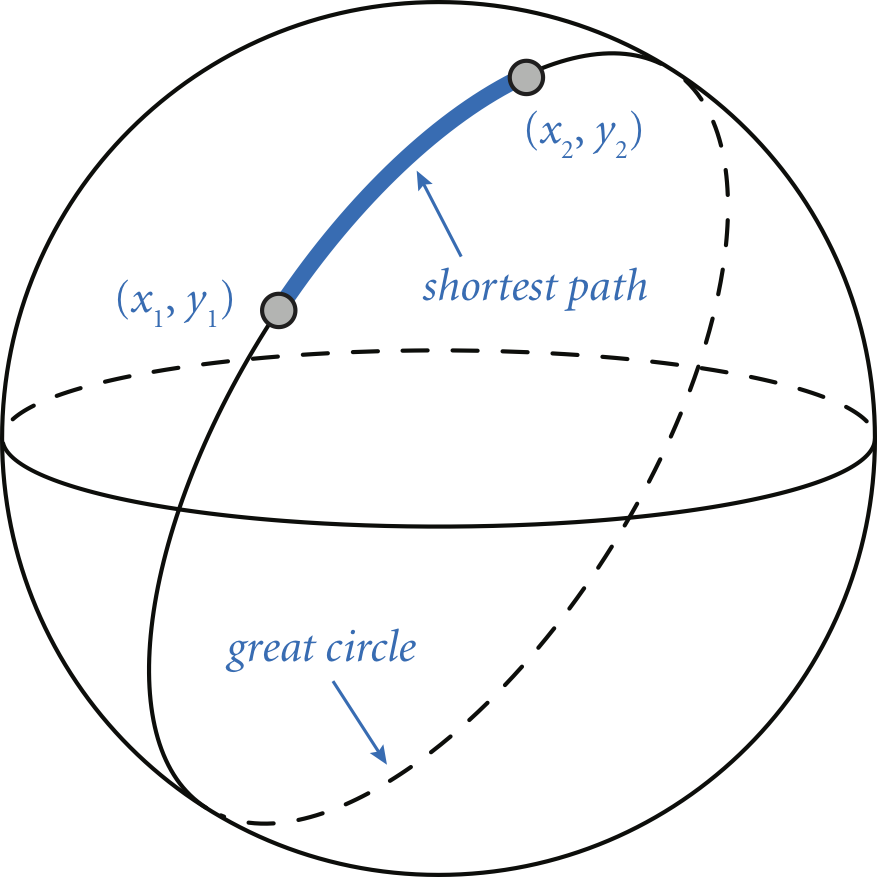
The Haversine formula gives the great-circle distance:
$$ distance \; = \; 2r \arcsin \left ( \sqrt{ \sin^2 \left ( \frac{x_2 - x_1}{2} \right ) + \cos x_1 \cos x_2 \sin^2 \left ( \frac{y_2 - y_1}{2} \right ) } \right ) $$
Use the mean Earth radius $r = \text{6,371.0}$ kilometers, which gives a good approximation.
Q.The arguments are given in degrees but Java’s trig functions use radians. What can I do?
radians = Math.toRadians(degrees) to convert from degrees to radians.Q.Which Math library functions should I use?
Q.I’m getting the wrong result. How can I check my formula?
Create a small example that you can work out by hand. Then verify that each intermediate term matches.
Q.Can I use a different formula to compute the great-circle distance?
Musical Notes
Musical notes are the building blocks of music. In this assignment, each note is specified by its MIDI number and an instrument.
Implement Note.java as specified by the following API:
public class Note {
// Creates a note with the given MIDI number and instrument name.
public Note(int midiNumber, String instrumentName)
// Returns this note's MIDI number.
public int midi()
// Returns this note's frequency.
public double frequency()
// Plays this note to standard audio using the associated WAV file.
public void play()
// Returns this note's name (e.g., C or A#).
public String name()
// Returns this note's octave.
public int octave()
// Returns a new Note transposed by delta semitones.
public Note transpose(int delta)
// Returns a string representation of this note.
public String toString()
// Unit tests the Note data type.
public static void main(String[] args)
}
Here is additional information about the required behavior:
-
Corner cases. You may assume that all arguments are meaningful values (e.g., MIDI numbers are between 0 and 127).
-
Note names and octaves. Musicians often use scientific pitch notation, such as A4 for concert A (MIDI number 69) and C4 for middle C (MIDI number 60). Scientific pitch notation consists of a note name (C, C#, D, D#, E, F, F#, G, G#, A, A#, or B) followed by an octave number. Each octave contains 12 notes. The following (partial) table shows the mapping between the two notations:
MIDI pitch MIDI pitch MIDI pitch MIDI pitch MIDI pitch 36 C2 48 C3 60 C4 72 C5 84 C6 37 C#2 49 C#3 61 C#4 73 C#5 85 C#6 38 D2 50 D3 62 D4 74 D5 86 D6 39 D#2 51 D#3 63 D#4 75 D#5 87 D#6 40 E2 52 E3 64 E4 76 E5 88 E6 … 41 F2 53 F3 65 F4 77 F5 89 F6 … 42 F#2 54 F#3 66 F#4 78 F#5 90 F#6 43 G2 55 G3 67 G4 79 G5 91 G6 44 G#2 56 G#3 68 G#4 80 G#5 92 G#6 45 A2 57 A3 69 A4 81 A5 93 A6 46 A#2 58 A#3 70 A#4 82 A#5 94 A#6 47 B2 59 B3 71 B4 83 B5 95 B6 For the sake of brevity, we use only sharp accidentals (such as A#) for the note names, and not the equivalent flat accidentals such as (B♭).
-
String representation. Return a string consisting of the MIDI number, the note name, the octave, and the instrument in the following format:
"69 A4 (piano)". -
Play. Play the WAV file whose filename is the instrument name followed by the MIDI number, with extension
.wav. For example, for instrumentpianoand MIDI number69, callStdAudio.play('piano/piano69.wav). -
Frequency. The frequency $f$ corresponding to MIDI number $m$ is
$$ f \; = \; 440 \; \times \; 2^{\, (m - 69) \, / \, 12} $$
-
Transpose. Transposing a note with MIDI number $m$ by $\Delta$ semitones yields a note with MIDI number $m + \Delta$. This method must return a new
Noteobject; it must not modify the invokingNote. -
Test client. The
main()method must call every public method.
Q.How can I define constants that are global to a class?
private static final modifiers. For example: private static final int MINUTES_PER_HOUR = 60;Q.Which Math library functions should I use?
Math library that you need. The function ``Math.pow()` is particularly useful for computing frequency.Q.MIDI values go from 0 to 127, however the table provided only shows the relationship between MIDI and octaves from 36 to 95. Should we only focus on those MIDI values? Or are we expected to generalize the relationship for the other values as well?
Q.There are only instrument audio files for MIDI numbers 12 through 116. Are our programs purposefully not intended to play MIDI numbers 0 through 11 and 117 through 127?
Q.Do I need conditionals to determine a note name or octave?
name() and octave() without any if statements. If you a have large multiway if statement ladder, you are probably not finding the most elegant way to implement these methods. Consider using integer division/remainder and an array.Play These Notes
Your final task is to write a client program PlayTheseNotes.java that reads a sequence of notes from a
file, transposes them by a given $\Delta$, plays them on standard audio, and prints the transposed notes to
standard output.
The program takes three command-line arguments:
- the name of the input file
- the instrument name:
piano,guitar,clarinet, ormbira - the transposed amount $\Delta$ (in semitones)
Organize your client according to the following API:
public class PlayTheseNotes {
// Reads a sequence of notes from filename and returns them
// as an array, using the given instrument.
public static Note[] read(String filename, String instrument)
// Takes three command-line arguments (a filename, an instrument name,
// and a transposition amount delta), reads the notes; transposes them;
// plays them on standard audio; and prints the transposed notes.
public static void main(String[] args)
}
Here are some details about the API:
-
Approach. In
main(), first callread()to obtain an array ofNoteobjects for the specified instrument. Then, in order, transpose each note by $\Delta$, play it, and print it. -
Input file format. A notes file consists of a sequence of lines:
- The first line contains the number of notes.
- Each remaining line contains a MIDI number followed by a floating-point duration (in seconds), separated by whitespace.
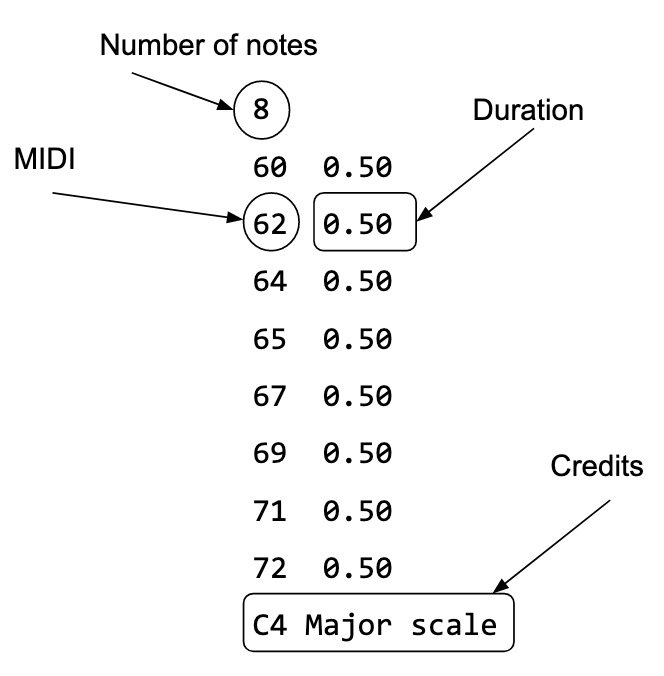
-
Input files. We provide several files containing simple songs in this format. You may also create and submit your own song in a file named
music.txt. It may be original or by another artist; include credits at the end of the file. -
Reading from a file. The
Indata type (Section 3.1) is an object-oriented version ofStdIn. UseIninread()since you will be reading from a file. -
Duration. Duration is typically used to represent note lengths (eighth notes, quarter notes, half notes, and whole notes). In this assignment, we provide only quarter notes. You must read the duration, but you will not use it when creating or playing notes.
-
Output. Print the transposed pitch (note name and octave) for each note as it plays. Print all pitches on one line, separated by single spaces, and end the line with a newline.
Here are some sample executions:
~/Desktop/oop> java-introcs PlayTheseNotes C4-major-scale.txt piano 0 C4 D4 E4 F4 G4 A4 B4 C5 ~/Desktop/oop> java-introcs PlayTheseNotes C4-major-scale.txt guitar 0 C4 D4 E4 F4 G4 A4 B4 C5 ~/Desktop/oop> java-introcs PlayTheseNotes C4-major-scale.txt piano 8 G#4 A#4 C5 C#5 D#5 F5 G5 G#5
Submission
Upload all files to TigerFile :
Tile.javaTracker.javaNote.javaPlayTheseNotes.javareadme.txtacknowledgments.txtmusic.txt(if you created your own composition)
Grading Breakdown
| File | Points |
|---|---|
| Tile.java | 10 |
| Tracker.java | 10 |
| Note.java | 10 |
| PlayTheseNotes.java | 6 |
| readme.txt | 4 |
| Total | 40 |
This assignment was developed by Kevin Wayne. Copyright © 2024-2026.