9. Hamming Codes in TOY

Download project ZIP | Submit to TigerFile

In this assignment, you will write TOY programs to encode and decode messages using Hamming codes. You will learn about machine-language programming and error-correcting codes.

Getting Started

Read Chapter 6 of the textbook and review the corresponding lectures and precepts.
Download and unzip hamming.zip , then open the hamming project in IntelliJ.
Review HammingEncoder.java and HammingDecoder.java in the project folder; they illustrate the encoding and decoding procedures in Java.
Refer to the TOY reference card, as needed.
Follow these partnering rules.

Background

Error-correcting codes enable reliable communication over noisy channels. The sender appends redundant information so the receiver can recover the original message even if some bits are corrupted during transmission. Errors can arise from static on a cell phone or atmospheric interference. In noisy settings, error-correcting codes can increase throughput by reducing (or eliminating) retransmissions. They are used in many systems, including memory storage systems (e.g., DRAM and SSDs), mobile and wireless communications, and digital television.

A Hamming code is an error-correcting code that detects and corrects single-bit errors. It is used in settings where such errors are common, including DRAM chips and satellite communications. A Hamming code takes four message bits and adds three parity bits to form a 7-bit codeword. If at most one of these seven bits is corrupted, the receiver can detect the error and recover the original four message bits. This single-bit error correction increases bandwidth by 75% (three extra parity bits for every four message bits). By comparison, sending three copies of each bit and taking the majority value increases bandwidth by 200%.

Approach

Before describing the algebra of Hamming codes, we first visualize how the parity bits are computed using Venn diagrams. As an example, suppose we want to send the 4-bit message 1101. Label the message bits $m_1, m_2, m_3, m_4$, as in the diagram below:

Then add three parity bits $p_1, p_2, p_3$ so that each circle has even parity:

That is, the sum of the four bits inside each circle is even:

In this example, the parity bits are 1 (top), 0 (left), and 0 (right). So, instead of sending 1101, we send the 7-bit codeword 1101100.

Now suppose one bit is corrupted during transmission, so the receiver gets the codeword 1001100:

The receiver detects an error by checking the parity of the three circles. Moreover, the pattern of failed parity checks pinpoints which bit flipped, so the receiver can correct the error and recover the original four message bits:

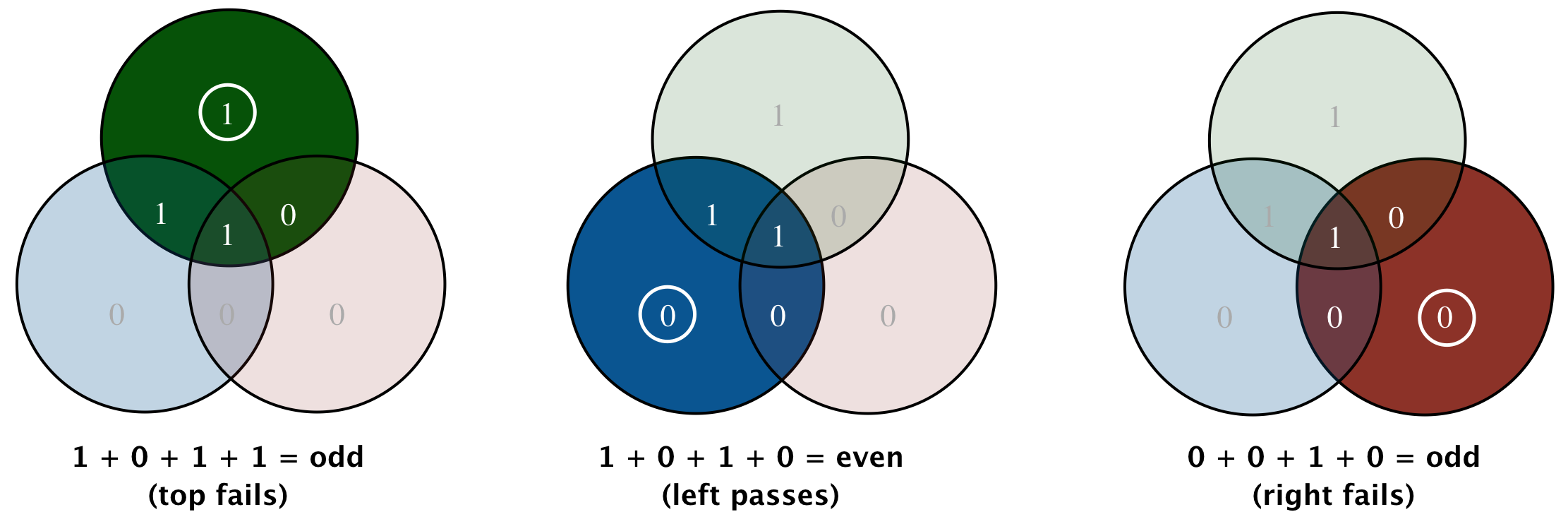
Here, the parity checks for the top and right circles fail, while the left circle passes. The only bit that lies in exactly those two circles is $m_2$, so the receiver flips $m_2$ to obtain 1101100. This corresponds to message bits 1101 plus parity bits 100, as intended.

The pattern of failed parity checks identifies which bit (if any) was flipped:

If no bit is corrupted, then all three parity checks pass.
If one of $m_1$, $m_2$, or $m_3$ is corrupted, then exactly two checks fail.
If $m_4$ is corrupted, then all three checks fail.
If one of $p_1$, $p_2$, $p_3$, or $p_4$ is corrupted, then exactly one check fails (the check for that circle).

This scheme corrects only single-bit errors; more sophisticated error-correcting codes handle multiple-bit errors.

Hamming Encoder

Write a TOY program encode.toy that encodes a binary message using the scheme described above.

Repeatedly read four bits $m_1, m_2, m_3, m_4$ from TOY standard input.
Compute the parity bits:
- $p_1 = m_1 \oplus m_2 \oplus m_4$
- $p_2 = m_1 \oplus m_3 \oplus m_4$
- $p_3 = m_2 \oplus m_3 \oplus m_4$
Write the seven bits $m_1, m_2, m_3, m_4, p_1, p_2, p_3$ to TOY standard output.
Stop when you read FFFF, then output FFFF.

Q.What is the meaning of the $\oplus$ operator?

It is the standard symbol in math and CS for exclusive or (xor), which is useful for comptuting parity. Xor takes two input bits and outputs 1 they are different and 0 if they are the same. Equivalently, it outputs 1 if the sum of the bits is odd, and 0 if is even. In Java and TOY, it corresponds to the ^ operator.

Hamming Decoder

Write a TOY program decode.toy that decodes (and corrects) a Hamming-encoded message.

Repeatedly read seven bits $m_1, m_2, m_3, m_4, p_1, p_2, p_3$ from standard input.
Recomptue the parity bits from the message bits:
- $q_1 = m_1 \oplus m_2 \oplus m_4$
- $q_2 = m_1 \oplus m_3 \oplus m_4$
- $q_3 = m_2 \oplus m_3 \oplus m_4$
Compare $q_1, q_2, q_3$ with the received parity bits $p_1, p_2, p_3$.
If necessary, flip the corrupted message bit, then write $m_1, m_2, m_3, m_4$ to standard output.
Stop when you read FFFF, then output FFFF.

To determine which message bit (if any) is corrupted, use the result of the three parity checks:

If zero or one check fails, then all four message bits are correct.
If checks 1 and 2 fail (but not check 3), then $m_1$ is incorrect.
If checks 1 and 3 fail (but not check 2), then $m_2$ is incorrect.
If checks 2 and 3 fail (but not check 1), then $m_3$ is incorrect.
If all three checks fail, then $m_4$ is incorrect.

Input Format

The input to encode.toy is a text file containing the bits to transmit.

Each line contains four bits, $m_1, m_2, m_3, m_4$.
Each bit is written as a 4-digit hexadecimal integer: 0000 (0) or 0001 (1), separated by whitespace.
The final line is the single integer FFFF, which marks the end of the file.

The file encode3.txt contains three 4-bit messages:

~/Desktop/hamming> more encode3.txt
0001 0001 0000 0001
0001 0001 0001 0000
0001 0001 0001 0001
FFFF

The corresponding 4-bit messages are 1101, 1110, and 1111.

The input format for decode.toy is similar, except that each line contains seven bits (a 7-bit codeword), again written as 0000 or 0001:

~/Desktop/hamming> more decode4.txt
0001 0001 0000 0001 0001 0000 0000
0001 0000 0000 0001 0001 0000 0000
0001 0001 0000 0000 0001 0000 0000
0001 0001 0000 0001 0001 0000 0001
FFFF

The corresponding 7-bit codewords are 1101100, 1001100, 1100100, and 1101101.

Formatting and Commenting Requirements

To make your TOY code readable and easy to debug, follow these formatting and commenting guidelines:

Each TOY instruction must have corresponding pseudocode. (If you use Visual X-Toy, the pseudocode is generated automatically.)
Add blank lines between logically related sections of TOY code.
Write a comment above each section explaining what that code does.
Use the third column for your own comments. Hint: use the Java code from HammingEncoder.java and HammingDecoder.java as a starting point for your comments.

FAQ

Q.Can I assume the input files are in the prescribed format?

Yes. The input files will contain only a sequence of 0000’s and 0001’s, followed by FFFF. If there are no bits to be decoded, the file contains only the single integer FFFF.

Q.How to use the Visual X-TOY Simulator?

Use the Visual X-TOY simulator by executing the following command in the IntelliJ terminal:

~/Desktop/hamming> java -jar toy.jar

The Visual X-TOY simulator provides lots of useful development features. There are two major modes: edit and debug. Use Mode > Edit Mode to edit .toy programs and Mode > Debug Mode to debug or run .toy programs. In Debug Mode, use the Reference, Stdin, Stdout and Core tabs on the right to help debug your program.

To open a TOY program from a file, use Select File > Open, then browse to find the program, e.g., multiply.toy.
To edit a TOY program, use Select Mode > Edit Mode. You can type your program directly in the edit window. Use multiply.toy as a reference for formatting and commenting.
To redirect standard input from a file, in Edit Mode, select Mode > Load File to Stdin.
To execute a TOY program, use Select Mode > Debug Mode. Then click the Run button at the bottom. You can enter data on standard input by typing the value in the Stdin tab and clicking the Add button. You will have to click the Run button to resume execution. You can see the results on standard output in the Stdout tab.

Q.What are common TOY programming issues?

The program counter starts at 10 so make sure that you place your code starting at memory address 10.
Be sure that each line follows the required format XX: XXXX.
Check for duplicated line numbers or out-of-order line numbers.
Check for using a letter like O or I instead of the number 0 or 1.
Remember that all values, memory addresses, and arithmetic are in hex. For example, memory address 1A follows 19. If you don’t specify the value for a memory address, that memory address will have the default value of 0000, which is a HALT instruction.
Watch out for jump statements — if you insert a new line of code between existing lines, you will have to renumber all the following lines. Also, be sure to update any jump statements that have hardwired line numbers.
Be very careful to update both your comments and your actual code at the same time! It is very common to update only the pseudocode and not the machine instruction.
All registers are global variables. One way to be sure that a register is not used for two different purposes is to fill in the question in the readme.txt about registers before or during debugging.

Q.I’m stuck. How do I make progress?

These are purely suggestions for how you might make progress. You do not have to follow these steps. If you get stumped or frustrated on some portion of the assignment, you should not hesitate to consult a preceptor.

Open the Visual X-Toy Simulator and experiment with some of the example programs.
1. Try the sample programs Add, Echo, and Sum by going to File > Open Example Programs.
2. Open and experiment with multiply.toy, which is included in the project folder.
3. Try executing some of the programs from precept.
Read, compile, and run the reference solutions HammingEncoder.java and HammingDecoder.java. Use these reference solutions as a design for your TOY programs.
The readme.txt provides tables to help your design/implementation/debugging of encode.toy and decode.toy. This will help you think about how you plan to use and/or re-use the Toy registers as you implement these Toy programs. Before you start coding, complete these tables, and update as needed. They will be very helpful for you as well as those helping you during office hours and/or Lab TA debugging sessions.
As you write your TOY programs, remember:
- The first column contains the TOY instruction in hex.
- The second column contains the TOY pseudo-code.
- The third column is used for your own comments. Write comments as you write your code. This will help you understand your design as well as help during office hours, grading, etc.
In X-Toy, create a new file (File > New).
Save the file (File > Save) as encode.toy in your Hamming assignment project folder.
Incrementally implement and test encode.toy, using HammingEncoder.java as a guide. Remember that as you revise your program, you will need to edit your TOY statement numbers accordingly.
- Write TOY code that reads a number from standard input. If the number is negative, the program shall halt. (Note, the only valid negative input is FFFF.) Otherwise, it prints the number and inputs the next number.
- Edit your TOY program from step (a) so that it now reads in sequences of four numbers, halting if the first number is negative. Otherwise, it writes the four numbers and inputs the next sequence of numbers.
- Edit your TOY program from step (b) so that it now computes the parity bits, and writes the parity bits.
Incrementally implement and test decode.toy, using HammingDecoder.java as a guide.

Q.How do I test my TOY programs?

We provide several input files for both encode.toy and decode.toy, along with the corresopnding answer files. For convenience, each answer file shows the input and an abbreviated version of the output. corresponding outputs.

Encoding

input file	output file
`encode0.txt`	`encode0-answer.txt`
`encode1.txt`	`encode1-answer.txt`
`encode3.txt`	`encode3-answer.txt`
`encode16.txt`	`encode16-answer.txt`

Decoding

input file	output file
`decode0.txt`	`decode0-answer.txt`
`decode1.txt`	`decode1-answer.txt`
`decode3.txt`	`decode3-answer.txt`
`decode4.txt`	`decode4-answer.txt`
`decode6.txt`	`decode6-answer.txt`
`decode16.txt`	`decode16-answer.txt`
`decode128.txt`	`decode128-answer.txt`

To test your TOY program with the command-line TOY.java simulator, type the commands below in the IntelliJ terrminal. You should see one bit (a TOY hex word) per line:

~/Desktop/hamming> java-introcs TOY encode.toy < encode3.toy
0001
0001
0000
0001
0001
0000
0000
0001
0001
0001
0000
0000
0000
0000
0001
0001
0001
0001
0001
0001
0001
FFFF

~/Desktop/hamming> java-introcs TOY decode.toy < decode4.toy
0001
0001
0000
0001
0001
0001
0000
0001
0001
0001
0000
0001
0001
0001
0000
0001
FFFF

You can then compare your output with the corresponding answer file.

The most thorough test is to encode and decode all possible inputs. The input files encode16.txt and decode128.txt do exactly that.

Submission

Upload all required files to TigerFile :

encode.toy
decode.toy
readme.txt
acknowledgments.txt

Be sure to answer all questions in readme.txt.

Grading Breakdown

Files	Points
encode.toy	16
decode.toy	22
readme.txt	2
Total	40

Leaderboard (optional)

Submit an optimized decode.toy to the Hamming Leaderboard for class fame and glory. You may work alone or with your partner. Your goal is to use the fewest nonzero words of TOY main memory.

Under 40 (decimal) is very good.
Under 35 is great.
The all-time record is 27.

To submit to the leaderboard and see results:

Upload nickname.txt containing your group name. Please keep it respectful.
Upload leaderboard.txt, describing your approach.
Submit to Leaderboard
View Current Leaderboard