7. Guitar Hero

Download project ZIP | Submit to TigerFile

In this assignment, you will simulate plucking a guitar string with the Karplus–Strong algorithm, turning your computer into a musical instrument. You will implement a ring buffer to support efficient simulation.

Getting Started

Review the partnering rules.
Download and unzip guitar.zip , then open the guitar project in IntelliJ.

Background and Approach

We model a vibrating guitar string as a discrete sequence of audio samples in a fixed-size buffer. The Karplus–Strong algorithm generates a plucked-string sound by repeatedly updating this buffer and playing the resulting samples as audio.

When a guitar string is plucked, it vibrates and produces sound. The string length determines its fundamental frequency $f$. We represent the string’s displacement using $n$ real-valued samples, where

\[ n = \left\lceil \frac{44100}{f} \right\rceil . \]

Plucking the string. To simulate the initial excitation, fill the $n$ samples with white noise: set each displacement to a random real number between $-0.5$ and $0.5$.

Simulating vibration (Karplus–String). Maintain a ring buffer of the $n$ samples. Repeatedly remove the first sample and append a new sample equal to the average of the removed sample and the new first sample, multiplied by an energy-decay factor (0.996). For example:

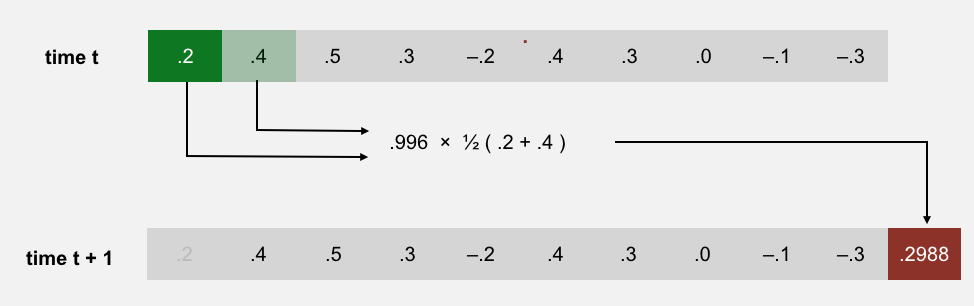
Q.Why does it work?

The Karplus–Strong algorithm works because of two features: feedback (via a ring buffer) and averaging.

Feedback (ring buffer). The ring buffer models a wave traveling back and forth along a string fixed at both ends. Its length sets the fundamental frequency, and the feedback reinforces that frequency and its harmonics. The energy-decay factor (0.996) models gradual energy loss.
Averaging. Each update averages adjacent samples, which acts as a gentle low-pass filter. Over time, this attenuates higher frequencies faster than lower ones, producing a realistic “plucked string” timbre.

From a mathematical-physics viewpoint, Karplus–Strong can be seen as a crude numerical approximation to the 1D wave equation.

Q.Why is the Karplus–Strong algorithm historically important?

It played a seminal role in the emergence of physically modeled sound synthesis, where a physical description of a musical instrument is used to synthesize sound electronically.

Ring Buffer

Your first task is to implement a data type that models a ring buffer. Write a class RingBuffer that implements the following API:

public class RingBuffer {

     // Creates an empty ring buffer with the given capacity.
     public RingBuffer(int capacity)

     // Returns the capacity of this ring buffer.
     public int capacity()

     // Returns the number of items currently in this ring buffer.
     public int size()

     // Is this ring buffer empty (size equals zero)?
     public boolean isEmpty()

     // Is this ring buffer full (size equals capacity)?
     public boolean isFull()

     // Adds x to the end of this ring buffer.
     public void enqueue(double x)

     // Removes and returns the item at the front of this ring buffer.
     public double dequeue()

     // Returns (but does not remove) the item at the front of this ring buffer.
     public double peek()

     // Tests this class by directly calling all instance methods.
     public static void main(String[] args)
}

Implementation strategy

Since the ring buffer has a fixed maximum capacity, you can implement it with a double[] array of that length. For efficiency, use cyclic wrap-around and maintain the following integer instance variables:

first: the index of the least recently inserted item (the front of the buffer)
last: the index one past the most recently inserted item (the end of the buffer)
size: the current number of items in the buffer

For example, here a ring buffer of size 4 with capacity 10:

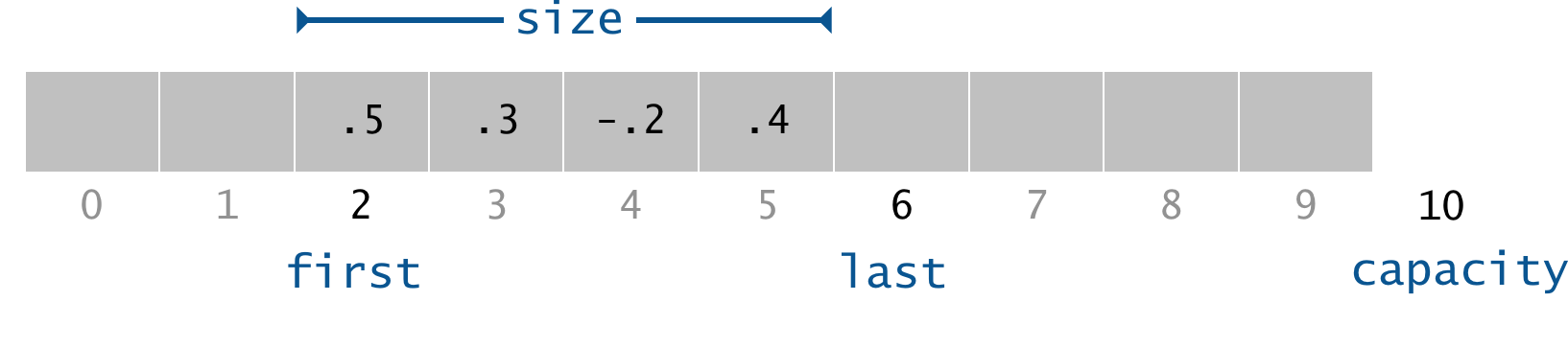
Insert. Store the new item at index last, then increment last.
Remove. Take the item at index first, then increment first.
Cyclic wrap-around. If first or last reaches capacity, wrap it to 0.

Requirements

Performance. The constructor must run in time proportional to the capacity. Every other method must run in constant item.
Data structure. You must use an array as the underlying data structure. You may not use ArrayList, LinkedList, or Queue.
Corner cases. RingBuffer must throw an IllegalStateException (with a custom message) if the client calls either dequeue() or peek() when the ring buffer is empty, or calls enqueue() when the ring buffer is full.
API. You must not add public methods.

Click here for possible progress steps.

Implementing `RingBuffer.java`

Implement RingBuffer in an incremental and iterative manner. Edit your initial RingBuffer.java so that it can compile (recall the Data.java exercise from precept). Then, implement one constructor/method at a time, together with at least one corresponding test in main(). We provide some test cases below. You should also include your own test cases in main(), such as the ones from the precept worksheet.
Define the instance variables you will need to represent a RingBuffer. Hint: review the worksheet from precept.
Implement the constructor for RingBuffer. You will need to allocate and initialize an array of doubles using the new operator. Observe that you have to do this in the constructor (and not when you declare the instance variables) because you do not know the length of the array until the constructor is called.
Test the constructor in main(). You can run this test by trying various RingBuffer sizes specified on the command line.

   // test for the constructor, based on command-line argument
   int n = Integer.parseInt(args[0]); // get the size of n from the command-line
   StdOut.printf("Test #0 - create a RingBuffer object with %d\n", n);
   RingBuffer buffer = new RingBuffer(n);

Implement capacity() and then test it:

   // test for capacity()
   StdOut.printf("Test #1 - check capacity - should be %d\n", n);
   StdOut.printf("**** Capacity is %d\n", buffer.capacity());

Implement size() and then test it:

   // test for size()
   StdOut.printf("Test #2 - check size - should be %d\n", 0);
   StdOut.printf("**** Size is %d\n", buffer.size());

Implement isFull() and enqueue() and then test them:

   // test for isFull() and enqueue()
   StdOut.printf("Test #3 - perform %d enqueues: 1.0, 2.0, ...\n", n);
   StdOut.printf("**** isFull() should be false- is %b\n", buffer.isFull());
   for (int i = 1; i <= n; i++) { // enqueue n values:  1.0, 2.0, ...
       buffer.enqueue(i);
       StdOut.printf("Test #3.%d - check size after %d enqueues- should be %d\n",
                        i, i, i);
       StdOut.printf("**** Size is %d\n", buffer.size());
   }
   StdOut.printf("**** isFull() should be true- is %b\n", buffer.isFull());

Implement isEmpty() and peek()` and then test them:

   // test for isEmpty() and peek()
   StdOut.printf("Test #4 - check peek value == %.1f\n", 1.0);
   StdOut.printf("**** isEmpty() should be false- is %b\n", buffer.isEmpty());
   double val1 = buffer.peek();
   StdOut.printf("**** Value is %.1f\n", val1);

Implement dequeue() and then test it:

   // test for dequeue()
   double val2 = buffer.dequeue();
   StdOut.printf("Test #5 - dequeue a value, then check value == %.1f and "
                      + "size == %d after a dequeue\n", 1.0, n - 1);
   StdOut.printf("**** Value is %.1f\n", val2);
   StdOut.printf("**** Size is %d\n", buffer.size());
   for (int i = 0; i < n - 1; i++) buffer.dequeue(); // dequeue everything left
   StdOut.printf("**** remove %d items and isEmpty() should be true- is %b\n",
                      n - 1, buffer.isEmpty());

Is the size of a RingBuffer equal to its capacity? The size is the number of elements currently in it; the capacity is its maximum possible size.

Is the size of a RingBuffer equal to the number of its non-zero elements? No. Some of the elements in the RingBuffer can be zero.

How do I throw a IllegalStateException with a custom message? Read the Exceptions paragraph on pages 465–466 of the textbook. Also, see the precept exercises for examples.

I get an ArrayIndexOutOfBoundsException or NullPointerException. What could cause this? Does your constructor correctly initialize all of the instance variables? Did you allocate memory for your array? Did you inadvertently re-declare an instance variable in a method or constructor, thereby shadowing the instance variable with the same name?

Guitar String

Create a data type to model a vibrating guitar string. Write a class GuitarString that implements the following API:

public class GuitarString {


    // Creates a guitar string of the given frequency, using a sampling
    // rate of 44,100. Initializes the ring buffer with ceil(44100 / frequency)
    // samples, all set to 0.0.
    public GuitarString(double frequency)

    // Creates a guitar string whose initial ring buffer values
    // are given by init[].
    public GuitarString(double[] init)

    // Returns the number of samples in the ring buffer.
    public int length()

    // Returns the current sample (the value at the front of the ring buffer)..
    public double sample()

    // Plucks this guitar string by replacing the ring buffer contents
    // with white noise (random values between -0.5 and +0.5).
    public void pluck()

    // Advances the Karplus-Strong simulation one time step.
    public void tic()

    // Tests this class by directly calling both constructors
    // and all instance methods.
    public static void main(String[] args)
}

Requirements

Data structures. Implement GuitarString using the RingBuffer data type. Do not use Stack, Queue, ArrayList, or other data types to represent a guitar string.
Karplus–Strong update. The tic() method method removes the sample at the front of the ring buffer, then adds to the end of the ring buffer the average of the removed sample and the new first sample, multiplied by the energy-decay factor (0.996).
API: you must not add public methods to the API.

Click here to show possible progress steps.

Implementing `GuitarString.java`

Again, employ an incremental/iterative implementation/testing/debugging approach. Edit your initial GuitarString.java so that it can compile (recall the Data.java exercise from precept). Then, implement one constructor/method at a time, together with at least one corresponding test in main().
Implement and test the GuitarString(double frequency) constructor, which creates a RingBuffer of the desired capacity n (the sampling rate 44,100 divided by the frequency, rounded up to the nearest integer), and initializes it to represent a guitar string at rest by enqueueing n zeros. (Use Math.ceil and cast the result to an integer.)
Implement the length() method, which returns the number of samples in the ring buffer.
Implement the sample() method, which returns the value of the item at the front of the ring buffer. Use peek().

How can I test the GuitarString(double frequency) constructor and these methods?

In main(), instantiate a few different GuitarString objects using the GuitarString(double frequency) constructor.
Invoke length() on each GuitarString object. Is the value returned by length() what you expect?
Invoke sample() on each GuitarString object. Is the value returned by sample() what you expect?

Implement and test the GuitarString(double[]) constructor, which creates a RingBuffer of capacity equal to the length n of the array, and initializes the contents of the ring buffer to the corresponding values in the array. In this assignment, this constructor’s primary purpose is to facilitate testing and debugging.

How can I test the GuitarString(double[]) constructor and these methods?

Instantiate a few different GuitarString objects using the GuitarString(double frequency) constructor.
Invoke length() on each GuitarString object. Is the value returned by length() what you expect?
Invoke sample() on each GuitarString object. Is the value returned by sample() what you expect?

Implement pluck(), which replaces the n items in the ring buffer with n random values between −0.5 and +0.5. Use a combination of RingBuffer methods including dequeue() and enqueue() to replace the buffer with values between −0.5 and 0.5. Hint: StdRandom

When generating random values between −0.5 and +0.5, should I include the two endpoints? The assignment specification does not specify, so you are free to choose whichever convention you find most convenient. In Java, we typically include the left endpoint of an interval and exclude the right endpoint. For example, StdRandom.uniformDouble(-0.5, 0.5) generates a uniformly random value in the interval $[−0.5, 0.5)$ and s.substring(i, j) returns the substring of the String s beginning at index i and ending at index j - 1.

How can I test the constructor and these methods?

Instantiate a GuitarString object.
Invoke length() and sample() on this object.
Next invoke pluck() on this object.
Next invoke length() and sample() again on each object. Are the values returned what you expect?
Try this with a few GuitarString objects.

Implement tic(). Use the enqueue(), dequeue(), and peek() methods. This method applies the Karplus–Strong update: delete the first sample from the ring buffer and adds to the end of the ring buffer the average of the deleted sample and the first sample, scaled by an energy decay factor.

How can I test the constructor and these methods?

Instantiate a GuitarString object.
Invoke length() and sample() on this object.
Next invoke tic() on this object.
Next invoke length() and sample() again on each object. Are the values returned what you expect?
Try this with a few GuitarString objects.

After you have implemented and tested each of the methods for GuitarString, run GuitarString using the test client in the Testing section.

Testing Your `GuitarString.java` Implementation

You can test your GuitarString data type using the following main(). Note - this test is not exhaustive, but it should help you debug.

// get frequency from command-line
double freq = Double.parseDouble(args[0]);


// create a GuitarString object with given frequency
StdOut.printf("Test #0 - create GuitarString obj with frequency %f\n", freq);
GuitarString gs1 = new GuitarString(freq);

// check length (sampling rate/frequency)
StdOut.printf("Test #1 - check length based on frequency %f\n", freq);
StdOut.printf("**** Length is %d\n", gs1.length());

// get one sample
StdOut.printf("Test #2 - check sample is %.1f\n", 0.0);
StdOut.printf("**** Sample is %.1f\n", gs1.sample());

// create a simple GuitarString with 4 samples
double[] samples = { -0.7, +0.8, -0.9, +0.6 };
GuitarString gs2 = new GuitarString(samples);
int len = samples.length;
StdOut.printf("Test #3 - check length based on given samples == %d\n",
              len);
StdOut.printf("**** Length is %d\n", gs2.length());

// get a sample
StdOut.printf("Test #4 - check sample is %.2f\n", samples[0]);
StdOut.printf("**** Sample is %.2f\n", gs2.sample());

// now pluck and check length
gs2.pluck();
StdOut.printf("Test #5 - check length after pluck is still == %d\n",
              len);
StdOut.printf("**** Length is %d\n", gs2.length());

// check that a random sample is  [-0.5, +0.5)
StdOut.printf("Test #6 - check sample is range [-0.5, +0.5)\n");
StdOut.printf("**** Sample is %.2f\n", gs2.sample());

// test tic and sample
GuitarString gs3 = new GuitarString(samples);
StdOut.printf("Test #7 - check sample is %.2f\n", samples[0]);
StdOut.printf("**** Sample is %.1f\n", gs3.sample());
gs3.tic();
StdOut.printf("Test #8 - check sample is %.2f\n", samples[1]);
StdOut.printf("**** Sample is %.2f\n", gs3.sample());

// test 25 tics
int m = 25; // number of tics
double[] moreSamples =
        { 0.2, 0.4, 0.5, 0.3, -0.2, 0.4, 0.3, 0.0, -0.1, -0.3 };
StdOut.printf("Test #9 - test %d tics\n", m);
GuitarString gs4 = new GuitarString(moreSamples);
for (int i = 0; i < m; i++) {
    double sample = gs4.sample();
    StdOut.printf("%6d %8.4f\n", i, sample);
    gs4.tic();
}

Run this test from the command line with some input n:

java-introcs GuitarString 440
(Test #1 - Test #8 not shown)...

Test #9 - test 25 tics
     0   0.2000
     1   0.4000
     2   0.5000
     3   0.3000
     4  -0.2000
     5   0.4000
     6   0.3000
     7   0.0000
     8  -0.1000
     9  -0.3000
    10   0.2988
    11   0.4482
    12   0.3984
    13   0.0498
    14   0.0996
    15   0.3486
    16   0.1494
    17  -0.0498
    18  -0.1992
    19  -0.0006
    20   0.3720
    21   0.4216
    22   0.2232
    23   0.0744
    24   0.2232

`Guitar Hero Client

Implement an interactive guitar player. GuitarHeroLite.java is a GuitarString client that plays guitar sounds in real time. It relies on Keyboard.java, which provides a simple GUI for reading keystrokes. When the user types p or v, the program plucks the guitar string corresponding to middle C or concert A, respectively. Since multiple sound waves add by superposition, the program plays the sum of the active string samples.

Requirements

Write a program GuitarHero that is similar to GuitarHeroLite. It must support 37 notes on the chromatic scale from 110 Hz to 880 Hz.
On each time step, sum the samples of all strings and play the result.
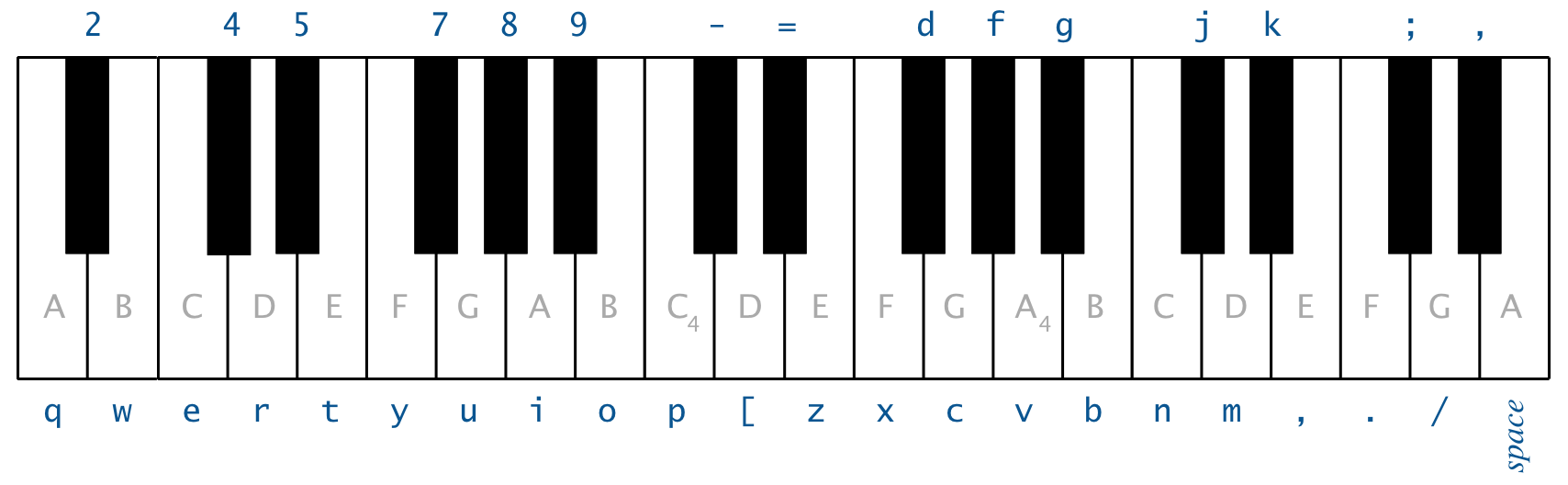
Use the following 37 keys (from lowest to highest note):

String keyboardString = "q2we4r5ty7u8i9op-[=zxdcfvgbnjmk,.;/' ";

This keyboard arrangement imitates a piano keyboard: the white keys are on the qwerty and zxcv rows, and the black keys are on the 12345 and asdf rows. For brevity, we name notes using sharps (e.g., A#) rather than the equivalent flats (e.g., B♭).
Character index i in keyboardString corresponds to the frequency $$ 440 \times 2^{(i − 24) / 12}\text{ } \text{ Hz} $$ Thus, 'q' is 110 Hz, 'i' is 220 Hz, and 'v' is 440 Hz.
Do not declare 37 individual GuitarString variables or write a 37-way if statement. Instead, create an array of 37 GuitarString objects and use keyboardString.indexOf(key) to determine which string to pluck.

Click here to show possible progress steps.

Implementing `GuitarHero.java`

Test GuitarString and RingBuffer using GuitarHeroLite. Which additional constructor and method does GuitarHeroLite test?
To implement GuitarHero.java, use the code in GuitarHeroLite.java as a starting point.
Create an array of GuitarString objects. Remember: to create an array of objects, you need to create the array, then you need to create each individual object.
Can you play individual notes? Do the notes have the correct frequencies? Can you play a chord?

Where do I play notes in GuitarHeroLite and GuitarHero? Be sure that the interactive Keyboard window has focus by clicking it. Then, either click the piano keys or type the keystrokes.

What happens if I call StdAudio.play(x) where x is greater than 1 or less than −1? The value is clipped – it is replaced by the value +1.0 or −1.0, respectively. This is fine and can happen when you play chords.

Why do I get a RuntimeException or an ArrayIndexOutOfBoundsException in GuitarHeroLite before I type any keystrokes? Did you forget to initialize the ring buffer to contain n zeros in your GuitarString constructor?

When I run GuitarHeroLite for the first time, I hear no sound. What am I doing wrong? Make sure you have tested with the main() provided for GuitarString. If that works, there is likely something wrong with pluck() since the main() provided for GuitarString does not test that method. To diagnose the problem, print the values of sample() and check that they become nonzero after you type the keystrokes p and v.

When I run GuitarHeroLite, I hear static (either just one click and then silence, or continual static). What am I doing wrong? It’s likely that pluck() is working, but tic() is not. The best test is to run the main() provided for GuitarString.

How do I use keyboardString.indexOf(key)? If keyboardString is a String and key is a character, then keyboardString.indexOf(key) returns the integer index of the first occurrence of the character key in the String keyboardString, or –1 if it does not occur. You can read about it in the String Javadoc page.

Can I hardwire the constants 44,100, 0.996, 440.0, and 37 in my program? As usual, we may deduct style points for using an unnamed constant, especially if you use it more than once. We recommend using SAMPLING_RATE for 44100, DECAY_FACTOR for 0.996, CONCERT_A for 440.0, and the expression keyboardString.length() for 37. You do not need to name all of the constants in the formula: \[ 440 \times 2^{(i − 24)/12} \]

Rock on! Play your GuitarHero

Here are some example tunes you can play on your GuitarHero. Try these below, and then compose some of your own:

An A major chord.
```
 i - z    i
          -
          z
```

An A major scale.
```
i o - [ z d f v   v f d z [ - o i
```

Type the following into your guitar to get the beginning of Led Zeppelin’s Stairway to Heaven. Multiple notes in a column are dyads and chords.

                                              w q q
        8       u       7       y             o p p
i p z v b z p b n z p n d [ i d z p i p z p i u i i

What is this familiar melody? (S == space)

nn//SS/ ..,,mmn //..,,m //..,,m nn//SS/ ..,,mmn

Submission

Upload all required files to TigerFile :

RingBuffer.java
GuitarString.java
GuitarHero.java
readme.txt
acknowledgments.txt

Grading Breakdown

Files	Points
RingBuffer.java	12
GuitarString.java	12
GuitarHero.java	12
readme.txt	4
Total	40

Challenge

Write a program AutoGuitar.java that will automatically play music using GuitarString objects.

Requirements

You may use a .txt file and read it using the In data type.
The duration of your composition must be between 10 and 120 seconds. Since the sampling rate is 44,100 Hz, this translates to between 441,000 and 5,292,000 calls to StdAudio.play().
You may create chords, repetition, and phrase structure using loops, conditionals, arrays, and functions. Also, feel free to incorporate randomness.
You may also create a new music instrument by modifying the Karplus–Strong algorithm; consider changing the excitation of the string (from white noise to something more structured) or changing the averaging formula (from the average of the first two samples to a more complicated rule) or anything else you might imagine. See below for some ideas.

Enrichment

Click each item to expand.

Click again to collapse the answer.

Synthesizing Additional Instruments

Here are some approaches for synthesizing additional instruments. Some come from the paper of Karplus and Strong.

Harp strings: Flipping the sign of the new value before enqueueing it in tic() will change the sound from guitar-like to harp-like. You may want to play with the decay factors to improve the realism, and adjust the buffer sizes by a factor of two since the natural resonance frequency is cut in half by the tic() change.
Drums: Flipping the sign of a new value with probability 0.5 before enqueueing it in tic() will produce a drum sound. A decay factor of 1.0 (no decay) will yield a better sound, and you will need to adjust the set of frequencies used.
Guitars play each note on one of six physical strings. To simulate this you can divide your GuitarString instances into six groups, and when a string is plucked, zero out all other strings in that group.
Pianos come with a damper pedal which can be used to make the strings stationary. You can implement this by changing the decay factor on iterations where a certain key (such as Shift) is held down.
While we have used equal temperament, the ear finds it more pleasing when musical intervals follow the small fractions in the just intonation system. For example, when a musician uses a brass instrument to play a perfect fifth harmonically, the ratio of frequencies is $ 3/2 = 1.5$ rather than $2^{7/12} ∼ 1.49$). Write a program where each successive pair of notes has just intonation.

Related Work

ChucK. ChucK is a specialized programming language for real-time synthesis, composition, and performance originated by Ge Wang and Perry Cook at Princeton University. Here’s the Karplus–Strong algorithm in ChucK.
Slide flute. Here’s a description of a physically modeled slide flute by Perry Cook.
Electric guitar synthesis. In COS 325/MUS 315 Transforming Reality by Computer, Charlie Sullivan ‘87 extended the Karplus–Strong algorithm to synthesize electric guitar timbres with distortion and feedback. Here’s his Jimi Hendrix-ified version of The Star Spangled Banner.

This assignment was developed by Andrew Appel, Jeff Bernstein, Alan Kaplan, Maia Ginsburg, Ken Steiglitz, Ge Wang, and Kevin Wayne.

7. Guitar Hero

Getting Started

Background and Approach

Ring Buffer

Implementation strategy

Requirements

Implementing RingBuffer.java

Guitar String

Requirements

Implementing GuitarString.java

Testing Your GuitarString.java Implementation

`Guitar Hero Client

Requirements

Implementing GuitarHero.java

Rock on! Play your GuitarHero

Submission

Grading Breakdown

Challenge

Requirements

Enrichment

Implementing `RingBuffer.java`

Implementing `GuitarString.java`

Testing Your `GuitarString.java` Implementation

Implementing `GuitarHero.java`