6. Image Classifier
Download project ZIP
| Submit to TigerFile
In this assignment, you will implement the perceptron algorithm and use it to classify images, then evaluate its accuracy.
Getting Started
- Complete the Midsemester Survey.
- Read Sections 3.2 and 3.3 of the textbook.
- Review the partnering rules.
- Read/scan this entire project description before starting to code. This will provide a big picture before diving into the assignment!
- Review the ML lecture and precept exercises.
- Download and unzip classifier.zip
, then open the
classifierproject in IntelliJ. - Consult the Picture and Color APIs as needed.
Context
Classification is a core task in machine learning (ML): given an input (such as an image), predict which category it belongs to. For a familiar example of digit classification, try this web app:
.
Training and testing. In this assignment, you will implement the perceptron algorithm for handwritten digit classification using supervised learning. Supervised learning as two phases:
-
Training: learn a function that maps inputs to labels from labeled examples. For digit recognition, the training set contains 60,000 grayscale images (inputs) and their corresponding digits (labels). Here is a small subset:

-
Testing: evaluate the learned function by predicting labels for unseen inputs (not used for training).
Binary vs. multiclass classification. In binary classification, we assign each image to one of two classes (e.g., “6” vs. “not 6”). By convention, we use labels $+1$ (positive) and $-1$ (negative). In multiclass classification, we assign each image to one of $m$ classes, labeled $0, 1, …, m-1$. For handwritten digits, $m = 10$ and class $i$ corresponding to digit $i$.
Test error rate. Typically, the algorithm makes some prediction errors (e.g., predicting 9 when the handwritten digit is 6). An important quality metric is the test error rate: the fraction of test inputs that are misclassified. It measures how well the learned classifier generalizes from the training data to new inputs.

Perceptrons. A perceptron is a simplified model of a biological neuron. It takes an input vector vector $x = x_0, x_1, \ldots, x_{n-1}$ of $n$ real numbers and outputs a binary label $+1$ or $-1$. A perceptron is defined by a weight vector $w = w_0, w_1, \ldots, w_{n-1}$. It computes the weighted sum
$$ S = (w_0 \cdot x_0) + (w_1 \cdot x_1) + \cdots + (w_{n-1} \cdot x_{n-1}) $$
and outputs $+1$ if the sum is positive, and $-1$ otherwise.

For the handwritten-digit task, we train a perceptron to output $+1$ for images of a chosen target digit and $-1$ for all other digits. The input vector $x$ contains the grayscale values of each pixel in the image, and the weight vector $w$ is computed during training, as described in the next paragraph.
Perceptron algorithm. How do we choose the weight vector $w$ so that the perceptron makes accurate predictions? The key idea is to use labeled training data to refine the weights incrementally. Initialize all weights to 0, then process the training examples one at a time. For each labeled input vector $x$, there are three cases:
-
Correct prediction: The perceptron predicts the correct label $+1$ or $-1$. Leave $w$ unchanged.
-
False positive: The true label is $-1$ but the perceptron predicts $+1$. Update $w$ by subtracting $x$: $$ \text{for each } j, \text{ } w^\prime_j=w_j - x_j $$
-
False negative: The true label is $+1$ but the perceptron predicts $-1$. Update $w$ by adding $x$: $$ \text{for each } j, \text{ } w^\prime_j=w_j + x_j $$
Intuitively, we push $w$ away from false positives and toward false negatives.
Example. Here is an example trace of the perceptron algorithm using four labeled inputs, each of length $n = 3$. In this example, an input $x$ has a label $+1$ if and only if $x_0 \le x_1 \le x_2$; otherwise it has a label $-1$.

Perceptron Data Type
Create a data type that represents a perceptron by implementing the following API:
public class Perceptron {
// Creates a perceptron with n input and all weights initialized to 0.
public Perceptron(int n)
// Returns the number of inputs n.
public int numberOfInputs()
// Returns the weighted sum (dot product) of the weight vector and x.
public double weightedSum(double[] x)
// Predicts the binary label for the input vector x.
// Returns +1 if the weighted sum is positive; otherwise returns -1.
public int predict(double[] x)
// Trains this perceptron on the input vector x with the given
// binary label (+1 or -1). Updates the weight vector according
// to the perceptron training rule.
public void train(double[] x, int binaryLabel)
// Returns a string representation of the weight vector, with the
// individual weights separated by commas and enclosed in parentheses.
// Example: (2.0, 1.0, -1.0, 5.0, 3.0)
public String toString()
// Tests this class by directly calling all instance methods.
public static void main(String[] args)
}
Corner cases. You may assume that all arguments to the constructor and instance methods are valid. For example, you may assume that every binary label is either $+1$ or $-1$, every input vector $x$ has length $n$, and $n \ge 1$.
Q.I’m stuck on Perceptron.java. Can you suggest some steps for making steady, incremental progress?
These steps are optional. Use them as needed.
Implementing Perceptron.java
-
Implement the
Perceptron()constructor and the methodnumberOfInputs().- Define two instance variables: an integer
nand real-valued arrayweights[]. - Initialize the instance variables.
- Test: In
main(), create a fewPerceptronobjects and print the number of inputs for each one.
- Define two instance variables: an integer
-
Implement the
toString()method.- Use a loop to concatenate the individual weights.
- Test: In
main(), print thePerceptronobjects you created in Step 1.
-
Implement the
weightedSum()method.- Use a loop to compute the weighted sum.
- Test: In
main(), callweightedSum()with different arguments and print the results.
-
Implement the
predict()method by callingweightedSum(). -
Implement the
train()method. Thetrain()method should callpredict(). -
Test: Use the code in the Testing section below to test
predict()andtrain(). -
Submit to TigerFile for additional testing.
Testing Perceptron.java
The Java code below trains a Perceptron on four input vectors (each of length three),
following the example in the assignment specification.
After Tests 1–3 pass, implement Tests 4–6.
// Create a Perceptron with n inputs.
int n = 3;
Perceptron perceptron = new Perceptron(n);
StdOut.printf("Test 1: Perceptron(%d)\n", n);
StdOut.println(" expect: " + "(0.0, 0.0, 0.0)");
StdOut.println(" result: " + perceptron);
StdOut.println("Test 2: numberOfInputs()");
StdOut.println(" expect: " + n);
StdOut.println(" result: " + perceptron.numberOfInputs());
double[] training1 = { 3.0, 4.0, 5.0 }; // +1 (yes)
double[] training2 = { 2.0, 0.0, -2.0 }; // -1 (no)
double[] training3 = { -2.0, 0.0, 2.0 }; // +1 (yes)
double[] training4 = { 5.0, 4.0, 3.0 }; // -1 (no)
StdOut.println("Test 3a: weightedSum(3.0, 4.0, 5.0)");
StdOut.println(" expect: " + 0.0);
StdOut.println(" result: " + perceptron.weightedSum(training1));
StdOut.println("Test 3b: predict(3.0, 4.0, 5.0)");
StdOut.println(" expect: " + -1);
StdOut.println(" result: " + perceptron.predict(training1));
StdOut.println("Test 3c: train(3.0, 4.0, 5.0, +1)");
perceptron.train(training1, +1);
StdOut.println(" expect: " + "(3.0, 4.0, 5.0)");
StdOut.println(" result: " + perceptron);
// TODO: Implement Tests 4–6, following the pattern in Test 3.
// Test 4: weightedSum(training2), predict(training2), train(training2, -1)
// Test 5: weightedSum(training3), predict(training3), train(training3, +1)
// Test 6: weightedSum(training4), predict(training4), train(training4, -1)
Do not move onto MultiPerceptron until Perceptron is working properly.
Multiclass Classification
In the previous section, we used a single perceptron for a binary classification task. For a multiclass problem with $m$ classes, we use an array of $m$ perceptrons, one per class. Perceptron $i$ is trained to answer the binary question: is this image the digit $i$?

We train each perceptron independently and combine their outputs to make a multiclass prediction.
-
Multiclass training. Initialize all $m$ perceptrons with weight vectors of $0$. Then process the labeled training inputs one at a time. For an input vector $x$ with class label $i$
- Train perceptron $i$ on $x$ with binary label $+1$
- Train each of the other $m-1$ perceptrons on $x$ with binary label $-1$
In other words, for perceptron $k$, examples of class $k$ are positive and all other examples are negative.
-
Multiclass prediction. To classify an input vector $x$, compute the weighted sum for each of the $m$ perceptrons. Predict the class label of the perceptron with the largest weighted sum. We choose exactly one class, even if all weighted sums are negative.
This one-vs-all strategy decomposes a multiclass classification task into $m$ binary classification tasks. In computer science, this kind of decomposition is called a reduction; reductions like this are used throughout machine learning.
Example. Here is an example of a multi-perceptron with $m = 2$ classes and $n = 3$ inputs.

MultiPerceptron Data Type
Create a data type that represents a multi-perceptron by implementing the following API:
public class MultiPerceptron {
// Creates a multi-perceptron with m classes and n inputs.
public MultiPerceptron(int m, int n)
// Returns the number of classes m.
public int numberOfClasses()
// Returns the number of inputs n (length of the feature vector).
public int numberOfInputs()
// Predicts the class label for input vector x.
public int predictMulti(double[] x)
// Trains this multi-perceptron on input vector x
// with the given class label (between 0 and m-1).
public void trainMulti(double[] x, int classLabel)
// Returns a string representation of this multi-perceptron, with
// the string representations of the perceptrons separated by commas
// and enclosed in parentheses.
// Example with m = 2 and n = 3: ((2.0, 0.0, -2.0), (3.0, 4.0, 5.0))
public String toString()
// Tests this class by directly calling all instance methods.
public static void main(String[] args)
}
Here are some additional details about the API:
-
Ties. If two (or more) perceptrons tie for the largest weighted sum in
predictMulti(), return the index of one of them. -
Corner cases. You may assume that the arguments to the constructor and instance methods are valid. For example, you may assume that every class label is an integer between $0$ and $m-1$, every input vector $x$ has length $n$, and $m \ge 1$ and $n \ge 1$.
Q.I’m stuck on MultiPerceptron. Can you suggest some steps for making steady, incremental progress?
Implementing MultiPerceptron.java
-
Implement the
MultiPerceptron()constructor and the methodsnumberOfClasses()andnumberOfInputs().- Define three instance variables:
- an integer
m(number of classes) - an integer
n(length of the input feature vector) - an array of
Perceptronobjectsperceptrons[]
- an integer
- Initialize the instance variables.
- Test: In
main(), create a fewMultiPerceptronobjects and print the number of classes and inputs for each object.
- Define three instance variables:
-
Implement the
toString()method.- Use a loop to concatenate the
Perceptronobjects. - Test: In
main(), print theMultiPerceptronobjects from Step 1.
- Use a loop to concatenate the
-
Implement the
predictMulti()method. -
Implement the
trainMulti()method. -
Test: Test
predictMulti()andtrainMulti()with the code in the Testing section (below). -
Submit to TigerFile for additional testing.
Testing MultiPerceptron.java
The Java code below creates a MultiPerceptron object,
trains the MultiPerceptron on four input vectors (each of length three)
and then tests the MultiPerceptron on two input vectors (of length three)
following the examples in the assignment specification.
// Create a MultiPerceptron with m classes and n inputs.
int m = 2;
int n = 3;
MultiPerceptron mp1 = new MultiPerceptron(m, n);
// Constructor Test 1: create a MultiPerceptron and print it.
StdOut.printf("Constructor Test 1: MultiPerceptron(%d, %d)%n", m, n);
StdOut.println(" expect: ((0.0, 0.0, 0.0), (0.0, 0.0, 0.0))");
StdOut.println(" result: " + mp1);
// Constructor Test 2: check the number of classes.
StdOut.println("Constructor Test 2: numberOfClasses()");
StdOut.println(" expect: " + m);
StdOut.println(" result: " + mp1.numberOfClasses());
// Constructor Test 3: check the number of inputs.
StdOut.println("Constructor Test 3: numberOfInputs()");
StdOut.println(" expect: " + n);
StdOut.println(" result: " + mp1.numberOfInputs());
// Training data.
double[] training1 = { 3.0, 4.0, 5.0 }; // class 1
double[] training2 = { 2.0, 0.0, -2.0 }; // class 0
double[] training3 = { -2.0, 0.0, 2.0 }; // class 1
double[] training4 = { 5.0, 4.0, 3.0 }; // class 0
// Training Test 1 (class 1).
StdOut.println("Training Test 1: trainMulti((3, 4, 5), 1)");
mp1.trainMulti(training1, 1);
StdOut.println(" expect: ((0.0, 0.0, 0.0), (3.0, 4.0, 5.0))");
StdOut.println(" result: " + mp1);
// Training Test 2 (class 0).
StdOut.println("Training Test 2: trainMulti((2, 0, -2), 0)");
mp1.trainMulti(training2, 0);
StdOut.println(" expect: ((2.0, 0.0, -2.0), (3.0, 4.0, 5.0))");
StdOut.println(" result: " + mp1);
// Training Test 3 (class 1).
StdOut.println("Training Test 3: trainMulti((-2, 0, 2), 1)");
mp1.trainMulti(training3, 1);
StdOut.println(" expect: ((2.0, 0.0, -2.0), (3.0, 4.0, 5.0))");
StdOut.println(" result: " + mp1);
// Training Test 4 (class 0).
StdOut.println("Training Test 4: trainMulti((5, 4, 3), 0)");
mp1.trainMulti(training4, 0);
StdOut.println(" expect: ((2.0, 0.0, -2.0), (-2.0, 0.0, 2.0))");
StdOut.println(" result: " + mp1);
// Testing data.
double[] testing1 = { -1.0, -2.0, 3.0 };
double[] testing2 = { 2.0, -5.0, 1.0 };
// Testing Test 1 (expect class 1).
StdOut.println("Testing Test 1: predictMulti((-1, -2, 3))");
StdOut.println(" expect: 1");
StdOut.println(" result: " + mp1.predictMulti(testing1));
// Testing Test 2 (expect class 0).
StdOut.println("Testing Test 2: predictMulti((2, -5, 1))");
StdOut.println(" expect: 0");
StdOut.println(" result: " + mp1.predictMulti(testing2));
Image Classifier Data Type
Your final task is to implement ImageClassifier.java, which uses MultiPerceptron
to classify images. It must:
- Train on the labeled examples in a training data file.
- Test on the labeled examples in a testing data file.
- Print the misclassified images and the test error rate.
Organize your client according to the following API:
public class ImageClassifier {
// Creates an ImageClassifier from the given configuration file.
public ImageClassifier(String configFile)
// Returns the name of the class corresponding to the given class label.
public String classNameOf(int classLabel)
// Returns the feature vector (1D array) extracted from the given picture.
public double[] extractFeatures(Picture picture)
// Trains the classifier using the given training data file.
public void trainClassifier(String trainFile)
// Predicts the class label for the given picture.
public int classifyImage(Picture picture)
// Returns the test error rate on the given testing data file.
// Also prints the misclassified examples (see the specification).
public double testClassifier(String testFile)
// Tests this class using a configuration file, training file,
// and testing file.
public static void main(String[] args) {
ImageClassifier classifier = new ImageClassifier(args[0]);
classifier.trainClassifier(args[1]);
double testErrorRate = classifier.testClassifier(args[2]);
System.out.println("test error rate = " + testErrorRate);
}
}
Here are some details about the API:
-
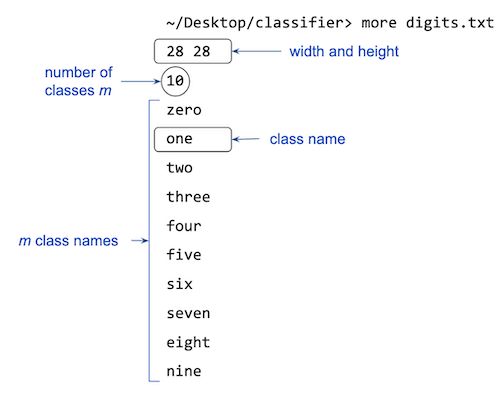
Configuration file format. The configuration file consists of the following lines:
- The image width and height (in pixels), used by the training and testing data files.
- The number of classes $m$.
- The names of the $m$ classes, one per line.
-
Training and testing file format. Training and testing data files consists of a sequence of lines. Each line contains:
- the name of an image file, and
- an integer class label (between $0$ and $m-1$), separated by whitespace.

For testing data files, you will use the integer labels only to evaluate the accuracy of your predictions.
-
Input files. We provide a variety of datasets in the specified format, including handwritten digits, fashion articles from Zalando, Hiragana characters, and doodles of fruit, animals, and musical instruments. The handwritten digits and fashion articles are included in your project folder. You can download the other datasets here.
Data files Description Examples Source digits.jar handwritten digits 
MNIST fashion.jar fashion articles 
Fashion MNIST Kuzushiji.jar Hirigana characters 
Kuzushiji MNIST fruit.jar fruit doodles 
Quick, Draw! animals.jar animal doodles 
Quick, Draw! music.jar musical instrument doodles 
Quick, Draw! -
Constructor. The
ImageClassifierconstructor takes one argument: the name of a configuration file. It reads the configuration data and creates aMultiPerceptronwith $m$ classes and $n = width \times height$ inputs. It also stores the class names from the configuration file. -
Feature extraction. The
extractFeatures()method converts a grayscale image into a one-dimensional feature vector for use withMultiPerceptron. It must:- iterate over the pixels in row-major order;
- extract the grayscale value of each pixel (for a shade of gray, the red, green, and blue components are equal); and
- store the values in a 1D array of length $width$-by-$height$.
It must throw an
IllegalArgumentExceptionif the image dimensions are not equal to the dimensions specified in the configuration file.
-
Training. The
trainClassifier()method takes the name of a training data file and trains the classifier using the images and labels in that file. -
Class name. The
classNameOf()method must throw anIllegalArgumentExceptionif its argument is not between $0$ and $m-1$, where $m$ is the number of classes. -
Classification. The
classifyImage()predicts and returns a class label $i$, where $$0 \leq i \leq m - 1$. -
Testing. The
testClassifier()method takes the name of a testing data file and tests the classifier using the images and labels in that file. For each misclassified image, it must print:- the image filename,
- the correct class name, and
- the predicted class name.
in the format shown below:
jar:file:digits.jar!/testing/6/4814.png, label = seven, predict = nine jar:file:digits.jar!/testing/6/66.png, label = seven, predict = eight jar:file:digits.jar!/testing/5/9982.png, label = six, predict = seven jar:file:digits.jar!/testing/7/6561.png, label = eight, predict = tenThe
testClassifier()method also returns the test error rate (the fraction of test images that are misclassified). -
Main. The
main()method takes three command-line arguments:- the name of a configuration data file;.
- the name of training data file;
- The name of testing data file.
It then creates an
ImageClassifier, trains it on the training data, tests it on the testing data, and prints the test error rate.Here is a sample execution:
~/Desktop/classifier> java-introcs ImageClassifier digits.txt digits-training20.txt digits-testing10.txt digits/testing/1/46.png, label = one, predict = three digits/testing/7/36.png, label = seven, predict = two digits/testing/7/80.png, label = seven, predict = two digits/testing/1/40.png, label = one, predict = two digits/testing/1/39.png, label = one, predict = three digits/testing/7/79.png, label = seven, predict = two digits/testing/9/20.png, label = nine, predict = two digits/testing/9/58.png, label = nine, predict = four test error rate = 0.8
Q.I’m stuck on ImageClassifier. Can you suggest some steps for making steady, incremental progress?
These steps are optional. Use them as needed.
Constructor and Instance Variables
-
Implement the
ImageClassifier()constructor. -
Read the configuration file data, and store the configuration data in your instance variables.
- Review the
Indata type from Section 3.1, which is an object-oriented version ofStdIn. - Define these instance variables:
- an integer
width(picture width) - an integer
height(picture height) - an array of strings
classNames[](the $m$ class names) - a
MultiPerceptronwith $m$ classes and $n = width \times height$ inputs
- an integer
-
Print the instances variables to standard output.
-
Test: In
main(), create variousImageClassifierobjects using different configuration files (image3x3.txt,digits.txt,fashion.txt, etc.) -
Implement
classNameOf(). For the given class label, return the class name associated with it. Test: call ``classNameOf()` with different arguments and print the results. -
Printing is solely for checking progress; remove the print statements once you have confidence your constructor is working properly.
Feature Extraction
-
Review Section 3.1 of the textbook, especially Program 3.1.4 (
Grayscale.java) for using the Picture and Color data types. Note that the images are already grayscale, so you don’t need to useLuminance.java. In particular, the red, green, and blue components are equal, so you can use any ofgetRed(),getGreen(), orgetBlue()to get the grayscale value. -
Comment out the test client code provided in
ImageClassifier.main(). -
Create a
Pictureobject for the image49785.png(in the project folder) and display it in a window. (Remove this code after you have successfully displayed the image.) -
Create a
Pictureobject for the imageimage3x3.png(in the project folder) corresponding to the 3-by-3 example given below.
- Extract its width and height and print the values to standard output.
- Extract the grayscale values of the pixels and print. If it’s not already in row-major order, adjust your code so that it prints the values in the specified order.
- If you are using IntelliJ, do not type the
import java.awt.Color;statement that is normally needed to access Java’sColordata type. IntelliJ is pre-configured to automatically addimportstatements when needed (and remove them when not needed).
-
Create a one-dimensional array of length width x height and copy the grayscale values to the array. Print the values of this array to confirm you can create a vector (row-major order) of values from a
Pictureobject. -
Using the code from steps (4) and (5) as a guide, implement the method
extractFeatures()that takes aPictureas an argument and returns the grayscale values as adouble[]in row-major order. -
Write a
main()method that testsextractFeatures(). Usingimage3-by-3.png, yourmain()method should print the values returned byextractFeatures()as shown in the above figure:ImageClassifier test = new ImageClassifier("image3x3.txt"); // create a small test Picture image3x3 = new Picture("image3x3.png"); double[] values = test.extractFeatures(image3x3); // print the array values -
Once you are confident that
extractFeatures()works, remove your testing code before submitting the assignment to TigerFile.
Classifying Images
-
Implement the
classifyImage()method. For the given image, extract its features and use the multi-perceptron to predict its class label. -
Implement the
trainClassifier()method. Read the training file data just as you read the configuration file. For each training image, extract its corresponding features and train the classifier using the corresponding label. -
Implement the
testClassifier()method. Read the testing file data just as you read the configuration file. For each testing image, predict its class. Print each misclassified image to standard output and compute the error rate on these images.
Training and Testing using Large Datasets
Now for the fun part. Try the large training and testing files. Processing 60,000 images may take noticeable time.
Now, the fun part. Use large training and testing input files. Be prepared to wait for one (1) minute (or more) while your program processes 60,000 images.
~/Desktop/classifier> java-introcs ImageClassifier digits.txt digits-training60K.txt digits-testing10K.txt jar:file:digits.jar!/testing/6/4814.png, label = six, predict = zero jar:file:digits.jar!/testing/5/4915.png, label = five, predict = eight jar:file:digits.jar!/testing/6/2754.png, label = six, predict = zero ... jar:file:digits.jar!/testing/4/1751.png, label = four, predict = three jar:file:digits.jar!/testing/3/9614.png, label = three, predict = five jar:file:digits.jar!/testing/5/6043.png, label = five, predict = three test error rate = 0.1318
Don’t worry about the odd-looking filenames. They specify the location of an image stored inside a JAR file (Java Archive). Storing the images in a JAR is more efficient than working with hundreds of thousands of separate files.
For example, in jar:file:digits.jar!/training/7/4545.png, digits.jar is the JAR file,
and /training/7/4545.png is the path to the image within that JAR.
Try experimenting with the other datasets:
~/Desktop/classifier> java-introcs ImageClassifier fashion.txt fashion-training60K.txt fashion-testing10K.txt ... ~/Desktop/classifier> java-introcs ImageClassifier Kuzushiji.txt Kuzushiji-training60K.txt Kuzushiji-testing10K.txt ... ~/Desktop/classifier> java-introcs ImageClassifier music.txt music-training50K.txt music-testing10K.txt ... ~/Desktop/classifier> java-introcs ImageClassifier fruit.txt fruit-training30K.txt fruit-testing6K.txt ... ~/Desktop/classifier> java-introcs ImageClassifier animals.txt animals-training60K.txt animals-testing12K.txt ...
Analysis
Answer Parts 1, 2 and 3 in readme.txt.
Part 1: Run the following experiment (you may want to redirect standard output to a file):
~/Desktop/classifier> java-introcs ImageClassifier digits.txt digits-training60K.txt digits-testing1K.txt
- Which digit is misclassified the most frequently?
- For that digit, what are the two most common incorrect predictions (i.e., which two digits does your classifier confuse it with most often)?
- Inspect several of these misclassified images. Explain what visual features might be causing the misclassifications.
Part 2. Use experiments to answer the following:
-
What is the error rate on
digits-testing1K.txtbefore training? To measure this, run your program without training (e.g., temporarily comment out the call totrainClassifier()inmain()). -
What is the error rate on
digits-testing1K.txtafter training? -
Based on these results, can you conclude that the classifier is learning? Explain briefly.
Part 3. People write the digit 7 in different ways. For example, some writers (common in parts of Europe and Latin America) draw a 7 with a horizontal bar through the middle, while others (common in Japan and Korea) draw a 7 with a slanted or “crooked” top stroke.
| Our data set | 7 with a middle bar | 7 with a crooked top |
|---|---|---|
 |
 |
 |
-
Suppose the training data contains no examples of either convention. How do you expect the classifier to perform on test data from populations that commonly use these styles? What are possible consequences?
-
Now consider a supervised learning system for diagnosing cancer. Suppose the training data contains examples only from population X, but you deploy the system on population Y. What are possible consequences?
Submission
Submit all files to TigerFile :
Perceptron.javaMultiPerceptron.javaImageClassifier.javareadme.txtacknowledgments.txt
Complete and submit the Midsemester Survey
Grading Breakdown
| Files | Points |
|---|---|
| Perceptron.java | 12 |
| MultiPerceptron.java | 12 |
| Classifier.java | 12 |
| readme.txt | 4 |
| Total | 40 |
Enrichment FAQ
Q.When was the perceptron algorithm first discovered?
Q.What is the significance of the perceptron algorithm?
It is a really simple, beautiful algorithm that, nevertheless, can do something interesting.
- The perceptron algorithm is one of the most fundamental algorithms in an area of ML called online learning (learning from samples one at a time).
- The perceptron algorithm is closely related to the support-vector machine algorithm, another fundamental ML algorithm.
- The perceptron algorithm has some beautiful theoretical properties. For example, if the training data set is linearly separable (i.e., there exists some weight vector that correctly classifies all of the training examples), and if we cycle through the training data repeatedly, the perceptron algorithm will eventually (and provably) find such a weight vector.
- Perceptrons are a building block in neural networks. In neural networks, many perceptrons (or other artificial neurons) are connected in a network architecture, in which the outputs of some neurons are used as the inputs to other neurons. Training multi-layer neural networks requires a more sophisticated algorithm to adjust the weights, such as gradient descent.
Q.Does the perceptron algorithm produce a different weight vector depending on the order in which it processes the training examples?
Q.Any intuition for why the perceptron algorithm works?
Geometrically, you can view each input vector $x$ as a point in $R^n$ and the weight vector $w$ as a hyperplane through the origin. The goal of the perceptron algorithm is to find a hyperplane that separates the positive examples from the negative examples. Using vector terminology, the weighted sum is known as the dot product; its sign determines on which side of the hyperplane the point lies.

During training, when we encounter a point $x$ that is on the wrong side of the hyperplane (i.e., a false positive or negative), we update the weight vector, thereby rotating the hyperplane slightly. After the rotation, x is either on the correct side of the hyperplane or, if not, at least a bit closer to the hyperplane (in terms of Euclidean distance).
Q.How can I improve accuracy of the perceptron algorithm?
Here are three simple ideas:
- Multiclass perceptron. Instead of training all
mperceptrons on each input vector, when there is a prediction error (multiclass perceptron predicts $i$ but correct label is $k$, train only two perceptrons: train perceptron $i$ (with label $-1$) and perceptron $k$ (with label $+1$). - Adjust the weights with a fraction of $+1$ or $-1$ for correct or incorrect predictions (this helps with a smoother convergence) and iterate over the training step multiple times, each time training the perceptron with the same set of training data (randomized in order).
- Normalize the Features array data to have values between 0 and 1 (divide the values with 255) and initialize the perceptron weights to random values (with uniform random or Gaussian random to be less than 1 and on average 0).
- Averaged perceptron. Instead of using the last weight vector, take the average of the weight vectors that are computed along the way.
- Incorporate more features. Instead of using the feature vector $x_0, x_1,\ldots, x_{n-1}$, create additional features. In particular, for each pair of features $x_i$ and $x_k$, create a new feature $x_{ik} = x_i * x_k$. You could also keep going, adding not just pairs of features, but also triples, etc. This can significantly improve accuracy, but it becomes prohibitively expensive in terms of computation.
See this paper for additional ideas, including the kernel trick and the voted-perceptron algorithm.
I noticed that the weights are always integral throughout the perceptron algorithm. Why is this?
Adding or subtracting an integer to an integer yields an integer. The weights are always adjusted by either adding or subtracting the input vector; for the image classification problems we consider in this assignment, the input vector elements are integers between 0 and 255 (grayscale values).As a perceptron is trained with more and more data, the weights increase in absolute value. Is this to be expected?
Yes. This implies that the algorithm makes smaller and smaller relative changes to the weights as it learns from more and more input–output pairs.Why not use the testing data for training?
We seek a model that can make good predictions for unseen input–output pairs. If we use the testing data when training, the algorithm could “memorize” the input–output pairs. While this might achieve higher accuracy on those inputs, the results may not generalize to unseen inputs.What is the difference between supervised and unsupervised learning?
In supervised learning, the algorithm has access to training data for which we know the correct labels. These labels act as a teacher supervising the learning process. In unsupervised learning, the training data is unlabeled, so there are no correct answers; instead, the goal may be to cluster similar inputs together.How can I make it recognize my own handwritten digits?
Use the same technique, but you must be careful to size-normalize and center the images, as is done in the MNIST training data.Can ML algorithms be trained to classify alphabetic and mathematical symbols?
Yes. Here are web apps that let you draw and find the most similar Unicode characters or LaTeX symbols.The current champion uses convolution neural networks and achieves a 99.79% accuracy rate on the MNIST testing database consisting of 10,000 images. Here are the 21 incorrect predictions:
There is not much room for improvement; indeed, some of the errors appear to be due to incorrectly labeled (or ambiguous) inputs.Any games based on classifying hand-drawn images?
Yes. Try Quick, Draw!, which uses neural networks and the world’s largest doodling data set.
What is the best performing algorithm for classifying handwritten digits using the MNIST dataset?
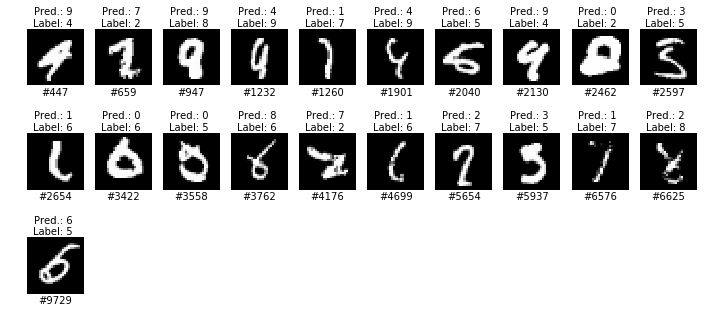
This assignment was developed by Sebastian Caldas, Robert DeLuca, Ruth Fong, Maia Ginsburg, Alan Kaplan, Kevin Jeon, and Kevin Wayne.
Copyright © 2005–2026