Kd-Trees Assignment

Create a symbol-table data type whose keys are two-dimensional points. Use a 2d-tree to support efficient range search (find all of the points contained in a query rectangle) and nearest-neighbor search (find a closest point to a query point). 2d-trees have numerous applications, ranging from classifying astronomical objects and computer animation to speeding up neural networks and data mining.

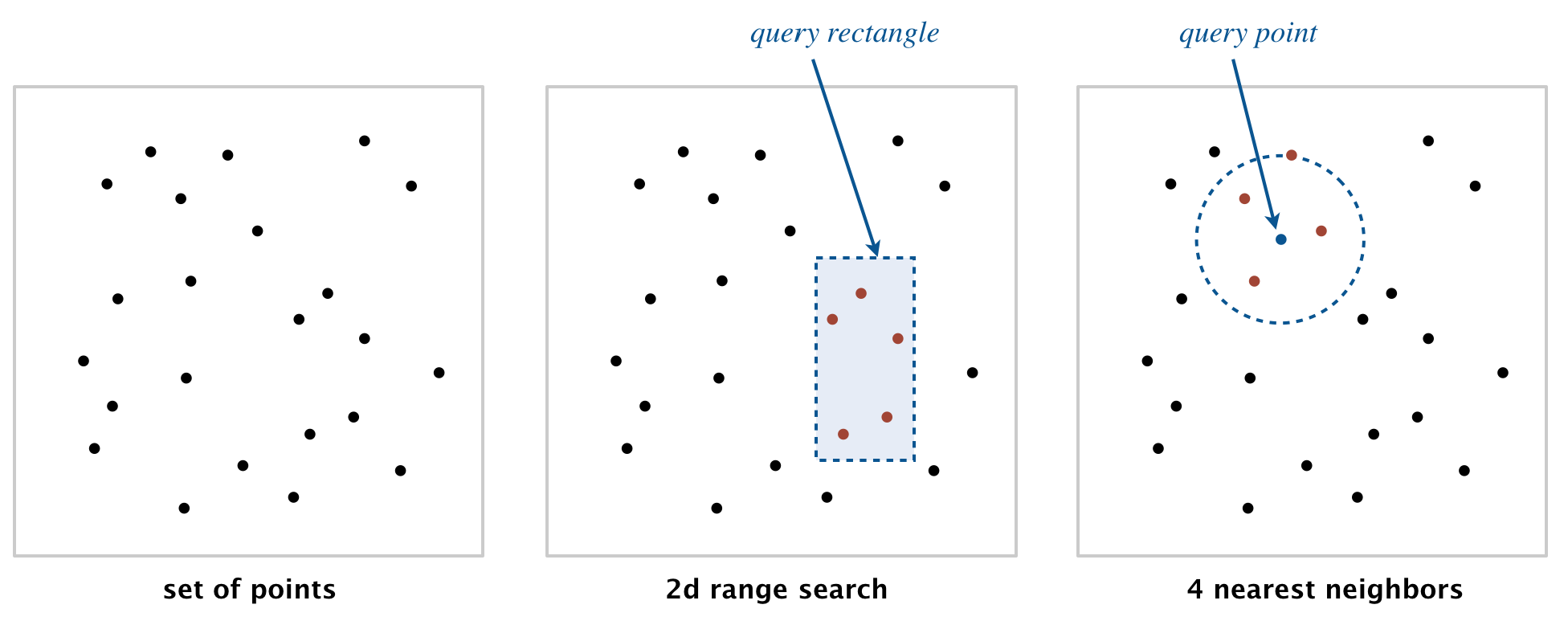
Geometric primitives. To get started, use the following geometric primitives for points and axis-aligned rectangles in the plane.

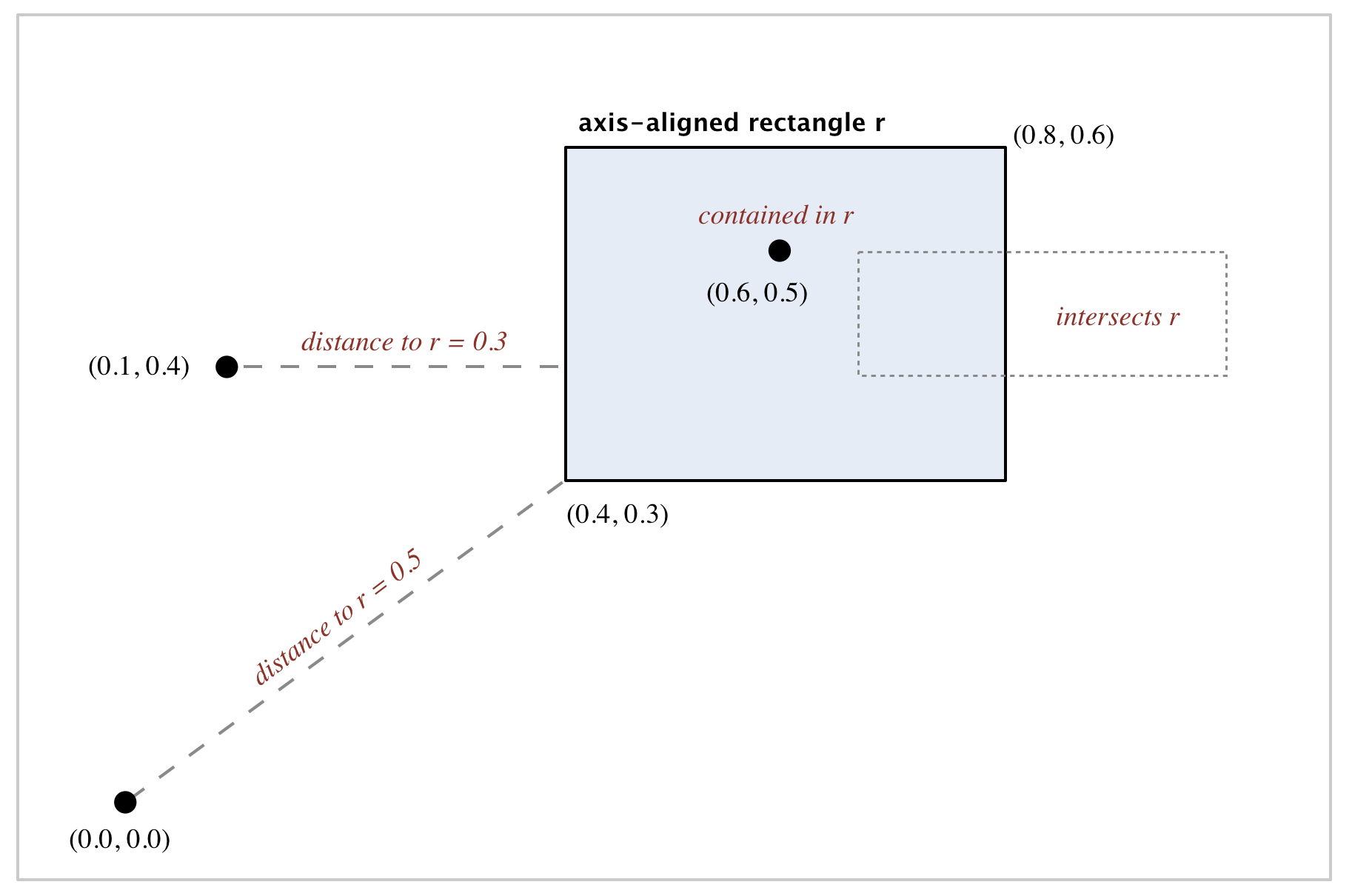
The immutable data type Point2D (part of algs4.jar) represents points in the plane. Here is the subset of its API that you may use:

public class Point2D implements Comparable<Point2D> {

    // construct the point (x, y)
    public Point2D(double x, double y)

    // x-coordinate 
    public double x()

    // y-coordinate 
    public double y()

    // square of Euclidean distance between two points 
    public double distanceSquaredTo(Point2D that)

    // for use in an ordered symbol table 
    public int compareTo(Point2D that)

    // does this point equal that object? 
    public boolean equals(Object that)

    // string representation 
    public String toString()

}

The immutable data type RectHV (part of algs4.jar) represents axis-aligned rectanges. Here is the subset of its API that you may use:

public class RectHV {
    // construct the rectangle [xmin, xmax] x [ymin, ymax] 
    public RectHV(double xmin, double ymin, double xmax, double ymax)

    // minimum x-coordinate of rectangle 
    public double xmin()

    // minimum y-coordinate of rectangle 
    public double ymin()

    // maximum x-coordinate of rectangle 
    public double xmax()

    // maximum y-coordinate of rectangle 
    public double ymax()

    // does this rectangle contain the point p (either inside or on boundary)? 
    public boolean contains(Point2D p)

    // does this rectangle intersect that rectangle (at one or more points)? 
    public boolean intersects(RectHV that)

    // square of Euclidean distance from point p to closest point in rectangle 
    public double distanceSquaredTo(Point2D p)

    // does this rectangle equal that object? 
    public boolean equals(Object that)

    // string representation 
    public String toString()

}

Do not modify these data types.

Brute-force implementation. Write a mutable data type PointST.java that uses a red–black BST to represent a symbol table whose keys are two-dimensional points, by implementing the following API:

public class PointST<Value> {

    // construct an empty symbol table of points 
    public PointST()

    // is the symbol table empty? 
    public boolean isEmpty()

    // number of points
    public int size()

    // associate the value val with point p
    public void put(Point2D p, Value val)

    // value associated with point p 
    public Value get(Point2D p)

    // does the symbol table contain point p? 
    public boolean contains(Point2D p)

    // all points in the symbol table 
    public Iterable<Point2D> points()

    // all points that are inside the rectangle (or on the boundary) 
    public Iterable<Point2D> range(RectHV rect)

    // a nearest neighbor of point p; null if the symbol table is empty 
    public Point2D nearest(Point2D p)

    // unit testing (required)
    public static void main(String[] args)

}

Implementation requirements. You must use either RedBlackBST or java.util.TreeMap; do not implement your own red–black BST.

Corner cases. Throw a java.lang.IllegalArgumentException if any argument is null.

Unit testing. Your main() method must call each public constructor and method directly and help verify that they work as prescribed (e.g., by printing results to standard output).

Performance requirements. In the worst case, your implementation must support size() in constant time; put(), get() and contains() in time proportional log n; and points(), nearest(), and range() in time proportional to n, where n is the number of points in the symbol table.

2d-tree implementation. Write a mutable data type KdTreeST.java that uses a 2d-tree to implement the same API (but renaming PointST to KdTreeST). A 2d-tree is a generalization of a BST to two-dimensional keys. The idea is to build a BST with points in the nodes, using the x- and y-coordinates of the points as keys in strictly alternating sequence, starting with the x-coordinates.

Search and insert. The algorithms for search and insert are similar to those for BSTs, but at the root we use the x-coordinate (if the point to be inserted has a smaller x-coordinate than the point at the root, go left; otherwise go right); then at the next level, use the y-coordinate (if the point to be inserted has a smaller y-coordinate than the point in the node, go left; otherwise go right); then at the next level, use the x-coordinate; and so forth.

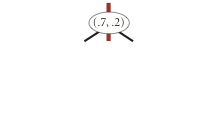
insert (0.7, 0.2)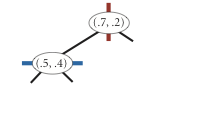
insert (0.5, 0.4)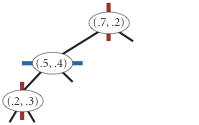
insert (0.2, 0.3)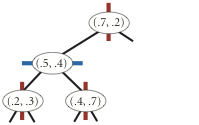
insert (0.4, 0.7)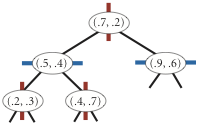
insert (0.9, 0.6)

Level-order traversal. The points() method must return the points in level order: first the root, then all children of the root (from left/bottom to right/top), then all grandchildren of the root (from left to right), and so forth. The level-order traversal of the above 2d-tree is (0.7, 0.2), (0.5, 0.4), (0.9, 0.6), (0.2, 0.3), (0.4, 0.7). This method is useful to assist you (when debugging) and us (when grading).

The prime advantage of a 2d-tree over a BST is that it supports efficient implementation of range search and nearest-neighbor search. Each node corresponds to an axis-aligned rectangle, which encloses all of the points in its subtree. The root corresponds to the entire plane [(−∞, −∞), (+∞, +∞ )]; the left and right children of the root correspond to the two rectangles split by the x-coordinate of the point at the root; and so forth.

Range search. To find all points contained in a given query rectangle, start at the root and recursively search for points in both subtrees using the following pruning rule: if the query rectangle does not intersect the rectangle corresponding to a node, there is no need to explore that node (or its subtrees). That is, search a subtree only if it might contain a point contained in the query rectangle.
Nearest-neighbor search. To find a closest point to a given query point, start at the root and recursively search in both subtrees using the following pruning rule: if the closest point discovered so far is closer than the distance between the query point and the rectangle corresponding to a node, there is no need to explore that node (or its subtrees). That is, search a node only if it might contain a point that is closer than the best one found so far. The effectiveness of the pruning rule depends on quickly finding a nearby point. To do this, organize the recursive method so that when there are two possible subtrees to go down, you choose first the subtree that is on the same side of the splitting line as the query point; the closest point found while exploring the first subtree may enable pruning of the second subtree.

Clients. You may use the following two interactive client programs to test and debug your code.

RangeSearchVisualizer.java reads a sequence of points from a file (specified as a command-line argument) and inserts those points into a 2d-tree. Then, it performs range searches on the axis-aligned rectangles dragged by the user in the standard drawing window.
NearestNeighborVisualizer.java reads a sequence of points from a file (specified as a command-line argument) and inserts those points into a 2d-tree. Then, it performs nearest-neighbor queries on the point corresponding to the location of the mouse in the standard drawing window.

Analysis of running time. Analyze the effectiveness of your approach to this problem by estimating how many many nearest-neighbor searches per second that each of your two implementations can perform for input1M.txt (1 million points), where the query points are uniformly random points in the unit square. Count only the time for the nearest-neighbor searches, not the time to read and insert the points.

Challenge for the bored. Add the following method to KdTreeST.java:

public Iterable<Point2D> nearest(Point2D p, int k)

This method returns the k points that are closest to the query point (in any order); return all n points in the data structure if n ≤ k. It must do this in an efficient manner, i.e. using the technique from kd-tree nearest neighbor search, not from brute force. Once you’ve completed this class, you’ll be able to run BoidSimulator.java (which depends upon both Boid.java and Hawk.java). Behold their flocking majesty.

Submission. Submit only PointST.java and KdTreeST.java. We will supply algs4.jar. Your may not call library functions except those in those in java.lang, java.util, and algs4.jar. Finally, submit a readme.txt file and answer the questions.

Grading.

file points

PointST.java 10

KdTreeST.java 24

readme.txt 6

40

file	points
`PointST.java`	10
`KdTreeST.java`	24
`readme.txt`	6
	40

Reminder: You can lose up to 4 points for poor style and up to 4 points for inadequate unit testing.

insert (0.7, 0.2)	insert (0.5, 0.4)	insert (0.2, 0.3)	insert (0.4, 0.7)	insert (0.9, 0.6)