COS 126
Recursive Graphics
|
Programming Assignment Checklist
Assignment Page
|
|
Frequently Asked Questions: Transform2D
|
What preparation do I need before beginning this assignment?
Read Sections 2.1–2.3 of the textbook.
The API expects the angles to be in degrees but Java's trigonometric functions assume
the arguments are in radians. How do I convert between the two?
Use Math.toRadians() to convert from degrees to radians.
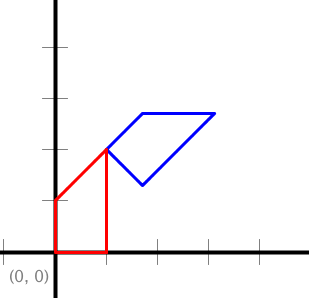
What is the purpose of the copy() function in Transform2D?
As noted in the assignment, the transformation methods mutate a given polygon.
This means that the parallel arrays representing the polygon are altered by the transformation methods.
It is often useful to save a copy of the polygon before applying a transform.
For example:
// Set the x- and y-scale
StdDraw.setScale(-5.0, 5.0);
// Original polygon
double[] x = { 0, 1, 1, 0 };
double[] y = { 0, 0, 2, 1 };
// Copy of original polygon
double[] cx = Transform2D.copy(x);
double[] cy = Transform2D.copy(y);
// Rotate, translate and draw the copy
Transform2D.rotate(cx, cy, -45.0);
Transform2D.translate(cx, cy, 1.0, 2.0);
StdDraw.setPenColor(StdDraw.BLUE);
StdDraw.polygon(cx, cy);
// Draw the original polygon
StdDraw.setPenColor(StdDraw.RED);
StdDraw.polygon(x, y);
|
 |
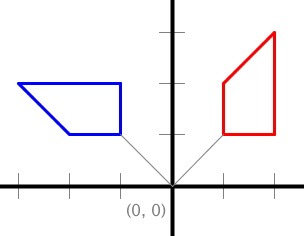
Does a polygon have to be located at the origin in order to rotate it?
No. You can rotate any polygon about the origin. For example:
// Original polygon
double[] x = { 1, 2, 2, 1 };
double[] y = { 1, 1, 3, 2 };
StdDraw.setPenColor(StdDraw.RED);
StdDraw.polygon(x, y);
// Rotate polygon
// 90 degrees counterclockwise
Transform2D.rotate(x, y, 90.0);
StdDraw.setPenColor(StdDraw.BLUE);
StdDraw.polygon(x, y);
|
 |
Does our code have to account for invalid arguments?
No. You can assume:
- the array passed to copy() is not null,
- arrays passed to scale(), translate() and rotate() are not null, are the same length, and do not contain the values NaN, Double.POSITIVE_INFINITY or Double.NEGATIVE_INFINITY.
- the values for the parameters alpha, theta, dx and dy are not NaN, Double.POSITIVE_INFINITY or Double.NEGATIVE_INFINITY.
|
Frequently Asked Questions: Sierpinski
|
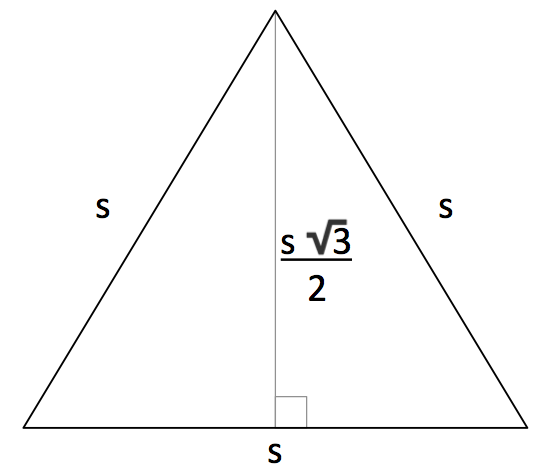
What is the formula for the height of an equilateral triangle of side length s?
The height is \(s \sqrt{3} / 2 \).
What is the layout of the initial equilateral triangle?
The top vertex lies at \((1/2, \sqrt{3} / 2)\)
You can use this diagram as a reference.
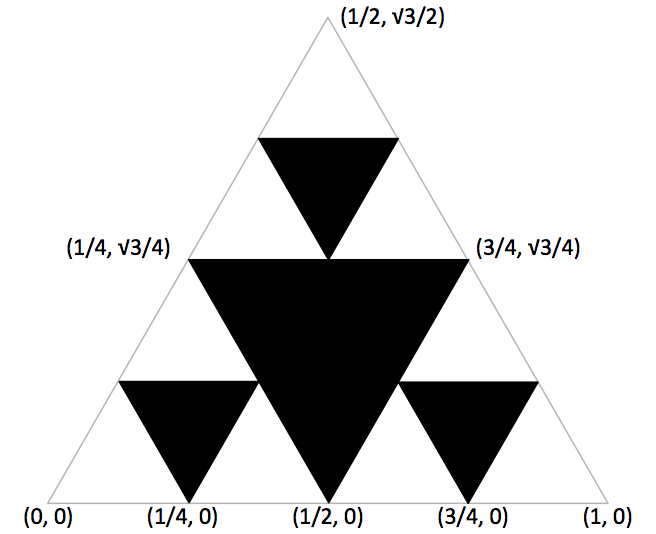
How do I draw a filled equilateral triangle?
Call the method StdDraw.filledPolygon() with appropriate arguments.
I get a StackOverflowError message even when n is a very small
number like 3. What could be wrong?
This means you are running out of space to store the function-call stack.
Often, this error is caused by an infinite recursive loop.
Have you correctly defined the base case and reduction step?
May I use different colors to draw the triangles?
Yes, you may use any colors that you like to draw either the outline
triangle or the filled triangles, provided it contrasts
with the white background.
|
Frequently Asked Questions: Art
|
The API checker says that I need to make my methods private. How do I do that?
Use the access modifier private instead of public in the method
signature. A public method can be called directly by a method in another class;
a private method cannot. The only public method that you should have
in Art is main().
How should I approach the artistic part of the assignment?
This part is meant to be fun, but here are some guidelines in case you're
not so artistic.
A very good approach is to first choose a self-referential pattern as a target output.
Check out the graphics exercises in
Section 2.3.
Here are some of our favorite
student submissions from a previous year.
See also the Famous Fractals in
Fractals Unleashed for some ideas.
Here is a
list of fractals, by Hausdorff dimension.
Some pictures are harder to generate than others (and some require trigonometry);
consult your preceptor for advice if you're unsure.
What will cause me to lose points on the artistic part?
We consider three things: the structure of the code; the structure of the
recursive function-call tree; and the art itself.
For example,
the
Quadricross looks very different from the in-class examples, but the
code to generate it looks extremely
similar to HTree, so it is a bad choice.
On the other hand,
even though the
Sierpinski curve
eventually generates something that looks like the Sierpinski triangle,
the code is very different (probably including an "angle" argument in the recursive method)
and so it would earn full marks.
You must do at least two of these things to get full credit on Art.java:
- call one or more Transform2D method
- use different parameters than our examples: f(n, x, y, size)
- use different StdDraw methods than in examples (e.g., ellipses, arcs, text)
- number of recursive calls not constant per level (e.g., conditional recursion)
- mutually recursive methods
- multiple recursive methods
- doesn't always recur from level n to level n-1
- draw between recursive calls, not just before or after all recursive calls
- use recursive level for secondary purpose (e.g. level dictates color)
Contrast this with the examples Htree, Sierpinski, and NestedCircles
which have very similar structures to one another.
You will also lose points if your artwork can be created just as easily
without recursion (such as
Factorial.java).
If the recursive function-call tree for your method is a straight line, it
probably falls under this category.
May I use GIF, JPG, or PNG files in my artistic creation?
Yes. If so, be sure to submit them along with your other files. Make
it clear in your readme.txt what part of the design is yours
and what part is borrowed from the image file.
How can I call the Transform2D methods inside Art.java?
You must fully qualify each method name with the Transform2D library. For example:
Transform2D.rotate(x, y, 45);
My function for Art.java takes several
parameters, but the assignment says that I can only
read in one command-line argument n. What should I do?
Choose a few of the best parameter values and do
something like the following:
if (n == 1) { x = 0.55; y = 0.75; }
else if (n == 2) { x = 0.55; y = 0.75; }
else if (n == 3) { x = 0.32; y = 0.71; }
else if ...
How can I create colors that aren't predefined in standard drawing?
It requires using objects that we'll learn about in Chapter 3.
In the meantime, you can use this
color guide.
|
Possible Progress Steps: Sierpinski
|
These are purely suggestions for how you might make progress. You do
not have to follow these steps.
Note that your final Sierpinski.java program should not be very long
(no longer than Htree, not including comments and blank lines).
- Review
Htree.java
from the textbook and lecture.
- Write the (non-recursive) function height() that takes the length
of the sides in an equilateral triangle as an argument and returns its height.
The body of this method should be a one-liner.
Test your height() function.
- Write a (nonrecursive) function
filledTriangle() that takes three real-valued arguments
(x, y, and length),
and draws a filled equilateral triangle (pointed downward)
with bottom vertex at (x, y) of the specified side length.
To debug and test your function, write main() so
that it calls filledTriangle() a few times, with different
arguments. You will be able to use this function without
modification in Sierpinski.java.
- Write a recursive function sierpinski() that
takes four (4) arguments (n, x, y, and length)
and plots a Sierpinski triangle of order n, whose
largest triangle has bottom vertex (x, y) and
the specified side length.
-
Write a recursive function sierpinski() that
takes one argument n, prints the value n,
and then calls itself three times with the value n-1.
The recursion should stop when n becomes 0.
To test this function out,
write main() so that it takes an integer command-line argument
n and calls sierpinski(n).
Ignoring whitespace,
you should get the
following output when
you call sierpinski() with n ranging
from 0 to 5.
Make sure you understand how this function works, and why it
prints the numbers in the order it does.
-
Modify sierpinski() so
that in addition to printing n, it also prints the length
of the triangle to be plotted.
Your function should now take two arguments: n
and length.
The initial call from main()
should be to sierpinski(n, 0.5) since the largest
triangle has side length 0.5.
Each successive level of recursion halves the length.
Ignoring whitespace,
your function should produce the
following output.
-
Modify sierpinski() so that it takes four (4) arguments
(n, x, y, and length)
and plots a Sierpinski triangle of order n, whose
largest triangle has bottom vertex (x, y) and
the specified side length.
Start by drawing Sierpinski triangles with pencil and paper.
Use the picture in the Q+A above to figure out the geometry of where the
smaller Sierpinski triangles should go.
-
Remove all print statements before submitting.
- Below are the target Sierpinski triangles for different values of n.
| |
% java-introcs Sierpinski 1
| % java-introcs Sierpinski 2
| % java-introcs Sierpinski 3
|
| |

| 
| 
|
- Transform2D.java: The main must call each of the methods defined by the Transform2D API.
- Sierpinski.java: Do not call
StdDraw.save(),
StdDraw.setCanvasSize(),
StdDraw.setXscale(),
StdDraw.setYscale(), or
StdDraw.setScale().
These method calls interfere with grading. (However, changing the x-
or y-scales in Transform2D.java and Art.java is permitted.)
- Art.java: Must
take exactly one integer command-line argument n
(which will be between
1 and 7).
- Be sure to include a comment just above each method definition
explaining what the method does—this will be required in
all future assignments as well.
Leaving a comment for main() is not required
since the header already does basically the same thing.
- Continue to follow the style guidelines from the assignment FAQ.
- Fractals in the wild.
Here's a
Sierpinski triangle in polymer clay,
a Sierpinski carpet cookie,
a fractal pizza,
and
a Sierpinski hamantaschen.
- Fractal dimension (optional diversion).
In grade school, you learn that the dimension of a line segment is 1,
the dimension of a square is 2, and the dimension of a cube is 3.
But you probably didn't learn what is really meant by the term dimension.
How can we express what it means mathematically or computationally?
Formally, we can define the Hausdorff dimension
or similarity dimension
of a self-similar figure by partitioning the figure into
a number of self-similar pieces of smaller size.
We define the dimension to be the
log (# self similar pieces) / log (scaling factor in each spatial direction).
For example, we can decompose the unit square into 4 smaller
squares, each of side length 1/2; or we can decompose it into 25 squares,
each of side length 1/5.
Here, the number of self-similar pieces is 4 (or 25) and
the scaling factor is 2 (or 5).
Thus, the dimension of a square is 2 since
log (4) / log(2) = log (25) / log (5) = 2.
We can decompose the unit cube into 8 cubes,
each of side length 1/2; or we can decompose it into 125 cubes,
each of side length 1/5.
Therefore, the dimension of a cube is log(8) / log (2) = log(125) / log(5) = 3.
We can also apply this definition directly to the (set of white
points in) Sierpinski triangle.
We can decompose the unit Sierpinski triangle into 3 Sierpinski triangles,
each of side length 1/2.
Thus, the dimension of a Sierpinski triangle is log (3) / log (2) ≈ 1.585.
Its dimension is fractional—more than a line segment, but less than a square!
With Euclidean geometry, the dimension is always an integer;
with fractal geometry, it can be something in between.
Fractals are similar to many physical objects;
for example, the coastline of Britain resembles
a fractal; its fractal dimension has been
measured
to be approximately 1.25.






