This assignments consists of three parts. First, write a library of static methods that performs geometric transforms on polygons. Next, write a program that plots a Sierpinski triangle. Finally, develop a program that plots a recursive pattern of your own design.

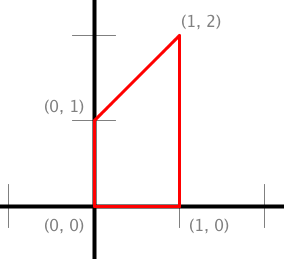
Part 1.   In this part, you will write a library of static methods that performs various geometric transforms on polygons. Mathematically, a polygon is defined by its sequence of vertices (x₀, y₀), (x₁, y₁), (x₂, y₂), …. In Java, we will represent a polygon by storing the x- and y-coordinates of the vertices in two parallel arrays x[] and y[].

// Represents the polygon with vertices (0, 0), (1, 0), (1, 2), (0, 1). double x[] = { 0, 1, 1, 0 }; double y[] = { 0, 0, 2, 1 };

Three useful geometric transforms are scale, translate and rotate.

• Scale the coordinates of each vertex (x_i, y_i) by a factor α.

  \( \begin{align*} x_i' \;&=\; \alpha \, x_i \\ y_i' \;&=\; \alpha \, y_i \end{align*} \)

• Translate each vertex (x_i, y_i) by a given offset (dx, dy).

  \( \begin{align*} x_i' \;&=\; x_i \;+\; dx \\ y_i' \;&=\; y_i \;+\; dy \end{align*} \)

• Rotate each vertex (x_i, y_i) by θ degrees counterclockwise, around the origin.

  \( \begin{align*} x_i' \;&=\; x_i \cos \theta \;-\; y_i \sin \theta \\ y_i' \;&=\; y_i \cos \theta \;+\; x_i \sin \theta \end{align*} \)

Write a two-dimensional transformation library Transform2D.java by implementing the following API:

public class Transform2D {

    // Returns a new array object that is an exact copy of the given array.
    // The given array is not mutated.
    public static double[] copy(double[] array)

    // Scales the polygon by the factor alpha.
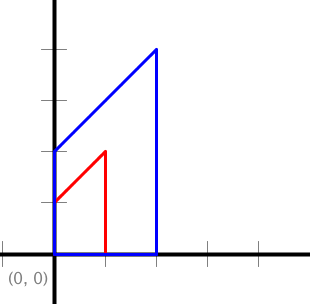
    public static void scale(double[] x, double[] y, double alpha)

    // Translates the polygon by (dx, dy).
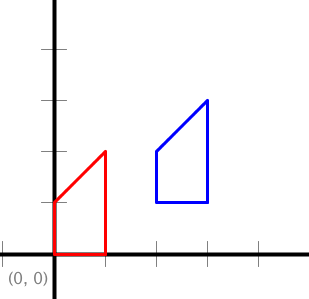
    public static void translate(double[] x, double[] y, double dx, double dy)

    // Rotates the polygon theta degrees counterclockwise, about the origin.
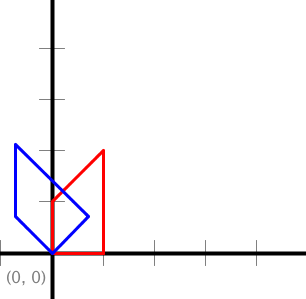
    public static void rotate(double[] x, double[] y, double theta)

    // Tests each of the API methods by directly calling them.
    public static void main(String[] args)
}

Note that the transformation methods scale(), translate() and rotate() mutate the polygons. Here are some example test cases (tests for copy() are not included:

// Scales polygon by the factor 2. StdDraw.setScale(-5.0, +5.0); double[] x = { 0, 1, 1, 0 }; double[] y = { 0, 0, 2, 1 }; double alpha = 2.0; StdDraw.setPenColor(StdDraw.RED); StdDraw.polygon(x, y); scale(x, y, alpha); StdDraw.setPenColor(StdDraw.BLUE); StdDraw.polygon(x, y);	// Translates polygon by (2, 1). StdDraw.setScale(-5.0, +5.0); double[] x = { 0, 1, 1, 0 }; double[] y = { 0, 0, 2, 1 }; double dx = 2.0, dy = 1.0; StdDraw.setPenColor(StdDraw.RED); StdDraw.polygon(x, y); translate(x, y, dx, dy); StdDraw.setPenColor(StdDraw.BLUE); StdDraw.polygon(x, y);	// Rotates polygon 45 degrees. StdDraw.setScale(-5.0, +5.0); double[] x = { 0, 1, 1, 0 }; double[] y = { 0, 0, 2, 1 }; double theta = 45.0; StdDraw.setPenColor(StdDraw.RED); StdDraw.polygon(x, y); rotate(x, y, theta); StdDraw.setPenColor(StdDraw.BLUE); StdDraw.polygon(x, y);

Part 2.   The Sierpinski triangle is an example of a fractal pattern like the H-tree pattern from Section 2.3 of the textbook.

order 1	order 2	order 3	order 4	order 5	order 6

API specification. When writing your program, exercise modular design by organizing it into four functions, as specified in the following API:

public class Sierpinski {

    //  Height of an equilateral triangle whose sides are of the specified length.
    public static double height(double length)

    //  Draws a filled equilateral triangle whose bottom vertex is (x, y)
    //  of the specified side length.
    public static void filledTriangle(double x, double y, double length)

    //  Draws a Sierpinski triangle of order n, such that the largest filled
    //  triangle has bottom vertex (x, y) and sides of the specified length.
    public static void sierpinski(int n, double x, double y, double length)

    //  Takes an integer command-line argument n;
    //  draws the outline of an equilateral triangle (pointed upwards) of length 1;
    //  whose bottom-left vertex is (0, 0) and bottom-right vertex is (1, 0); and
    //  draws a Sierpinski triangle of order n that fits snugly inside the outline.
    public static void main(String[] args)
}

Restrictions: You may not change either the scale or size of the drawing window.

Part 3.   In this part you will create a program Art.java that produces a recursive drawing of your own design. It must take one integer command-line argument n that controls the depth of recursion. It must stay within the drawing window when n is between 1 and 7. It can be a geometric pattern, a random construction, or anything else that takes advantage of recursive functions. For full marks, it must not be something that could be easily rewritten to use loops in place of recursion, and some aspects of the recursive function-call tree (or how parameters or overlapping are used) must be distinct from the in-class examples (HTree, Sierpinski, NestedCircles, Brownian).

Optionally, you may use the Transform2D library you implemented in Part 1. You may also define additional geometric transforms in Art.java, such as sheer, reflect across the x- or y- axis, or rotate about an arbitrary point.

Additional requirements: Your program must be organized into at least three separate functions, including main(). All functions except main() must be private.

Restrictions: You may not change the size of the drawing window (but you may change the scale). Do not add sound.

Submission.   Submit Transform2D.java, Sierpinski.java, and Art.java. If your Art.java requires any supplementary image files, submit them as well. Finally, submit a readme.txt file and answer the questions therein.

Challenge for the bored.   Write a program that plots Sierpinski triangles without using recursion.