Faster Dimension Reduction
![Blitz data map [article image]](fulltext_files/012010_galaxygarden_Faster_Dimension.jpg) Credit: The Galaxy Garden
Credit: The Galaxy Garden
Data represented geometrically in high-dimensional vector spaces can be found in many applications. Images and videos, are often represented by assigning a dimension for every pixel (and time). Text documents may be represented in a vector space where each word in the dictionary incurs a dimension. The need to manipulate such data in huge corpora such as the web and to support various query types gives rise to the question of how to represent the data in a lower-dimensional space to allow more space and time efficient computation. Linear mappings are an attractive approach to this problem because the mapped input can be readily fed into popular algorithms that operate on linear spaces (such as principal-component analysis, PCA) while avoiding the curse of dimensionality.
The fact that such mappings even exist became known in computer science following seminal work by Johnson and Lindenstrauss in the early 1980s. The underlying technique is often called "random projection." The complexity of the mapping itself, essentially the product of a vector with a dense matrix, did not attract much attention until recently. In 2006, we discovered a way to "sparsify" the matrix via a computational version of Heisenberg's Uncertainty Principle. This led to a significant speedup, which also retained the practical simplicity of the standard Johnson-Lindenstrauss projection. We describe the improvement in this article, together with some of its applications.
1. Introduction
Dimension reduction, as the name suggests, is an algorithmic technique for reducing the dimensionality of data. From a programmer's point of view, a d-dimensional array of real numbers, after applying this technique, is represented by a much smaller array. This is useful because many data-centric applications suffer from exponential blowup as the underlying dimension grows. The infamous curse of dimensionality (exponential dependence of an algorithm on the dimension of the input) can be avoided if the input data is mapped into a space of logarithmic dimension (or less); for example, an algorithm running in time proportional to 2d in dimension d will run in linear time if the dimension can be brought down to log d. Common beneficiaries of this approach are clustering and nearest neighbor searching algorithms. One typical case involving both is, for example, organizing a massive corpus of documents in a database that allows one to respond quickly to similar-document searches. The clustering is used in the back-end to eliminate (near) duplicates, while nearest-neighbor queries are processed at the front-end. Reducing the dimensionality of the data helps the system respond faster to both queries and data updates. The idea, of course, is to retain the basic metric properties of the data set (e.g., pairwise distances) while reducing its size. Because this is technically impossible to do, one will typically relax this demand and tolerate errors as long as they can be made arbitrarily small.
The common approaches to dimensionality reduction fall into two main classes. The first one includes data-aware techniques that take advantage of prior information about the input, principal-component analysis (PCA) and compressed sensing being the two archetypical examples: the former works best when most of the information in the data is concentrated along a few fixed, unknown directions in the vector space. The latter shines when there exists a basis of the linear space over which the input can be represented sparsely, i.e., as points with few nonzero coordinates.
The second approach to dimension reduction includes data-oblivious techniques that assume no prior information on the data. Examples include sketches for data streams, locality sensitive hashing, and random linear mappings in Euclidean space. The latter is the focus of this article. Programmatically, it is equivalent to multiplying the input array by a random matrix. We begin with a rough sketch of the main idea.
Drawing on basic intuition from both linear algebra and probability, it may be easy to see that mapping high-dimensional data into a random lower-dimensional space via a linear function will produce an approximate representation of the original data. Think of the directions contained in the random space as samples from a population, each offering a slightly different view of a set of vectors, given by their projection therein. The collection of these narrow observations can be used to learn about the approximate geometry of these vectors. By "approximate" we mean that properties that the task at hand may care about (such as distances and angles between vector) will be slightly distorted. Here is a small example for concreteness. Let a1,..., ad be independent random variables with mean 0 and unit variance (e.g., a Gaussian N(0, 1)). Given a vector x = (x1,..., xd), consider the inner product Z = Σiaixi: the expectation of Z is 0 but its variance is precisely the square of the Euclidean length of x. The number Z can be interpreted as a "random projection" in one dimension: the variance allows us to "read off" the length of x. By sampling in this way several times, we can increase our confidence, using the law of large numbers. Each sample corresponds to a dimension. The beauty of the scheme is that we can now use it to handle many distances at once.
It is easy to see that randomness is necessary if we hope to make meaningful use of the reduced data; otherwise we could be given as input a set of vectors belonging to the kernel of any fixed matrix, thus losing all information. The size of the distortion as well as the failure probability are user-specified parameters that determine the target (low) dimension. How many dimensions are sufficient? Careful quantitative calculation reveals that, if all we care about is distances between pairs of vectors and angles between them—in other words, the Euclidean geometry of the data—then a random linear mapping to a space of dimension logarithmic in the size of the data is sufficient. This statement, which we formalize in Section 1.1, follows from Johnson and Lindenstrauss's seminal work.25 The consequence is quite powerful: If our database contains n vectors in d dimensions, then we can replace it with one in which data contains only log n dimensions! Although the original paper was not stated in a computational language, deriving a naïve pseudocode for an algorithm implementing the idea in that paper is almost immediate. This algorithm, which we refer to as JL for brevity, has been studied in theoretical computer science in many different contexts. The main theme in this study is improving efficiency of algorithms for high-dimensional geometric problems such as clustering,37 nearest neighbor searching,24, 27 and large scale linear algebraic computation.18, 28, 35, 36, 38
For many readers it may be obvious that these algorithms are directly related to widely used technologies such as web search. For others this may come as a surprise: Where does a Euclidean space hide in a web full of textual documents? It turns out that it is very useful to represent text as vectors in high-dimensional Euclidean space.34 The dimension in the latter example can be as high as the number of words in the text language!
This last example illustrates what a metric embedding is: a mapping of objects as points in metric spaces. Computer scientists care about such embeddings because often it is easier to design algorithms for metric spaces. The simpler the metric space is, the friendlier it is for algorithm design. Dimensionality is just one out of many measures of simplicity. We digress from JL by mentioning a few important results in computer science illustrating why embedding input in simple metric spaces is useful. We refer the reader to Linial et al.29 for one of the pioneering works in the field.
- The Traveling Salesman Problem (TSP), in which one wishes to plan a full tour of a set of cities, with given costs of traveling between any two cities is an archetype of a computational hardness which becomes easier if the cities are embedded in a metric space,14 and especially in a low-dimensional Euclidean one.7, 30
- Problems such as combinatorial optimization on graphs become
easier if the nodes of the graph can be embedded in
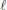 1 space. (The space
1 space. (The space
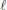 dp is defined to be the
set Rd endowed with a norm, where the
norm of a vector x (written as
||x||p) is given by
(Σdi=1|xi|p)1/p.
The metric is given by the distance between pairs of vectors
x and y taken to be ||x -
y||p.)
dp is defined to be the
set Rd endowed with a norm, where the
norm of a vector x (written as
||x||p) is given by
(Σdi=1|xi|p)1/p.
The metric is given by the distance between pairs of vectors
x and y taken to be ||x -
y||p.) - Embedding into tree metrics (where the distance between two nodes is defined by the length of the path joining them) is useful for solving network design optimization problems.
The JL algorithm linearly embeds an input which is already in
a high-dimensional Euclidean space
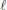 d2 into a lower-dimensional
d2 into a lower-dimensional
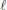 kp space for any
p ≥ 1, and admits a naïve implementation with
O(dk) running time per data vector; in other words,
the complexity is proportional to the number of random matrix
elements.
kp space for any
p ≥ 1, and admits a naïve implementation with
O(dk) running time per data vector; in other words,
the complexity is proportional to the number of random matrix
elements.
Our modification of JL is denoted FJLT, for Fast-Johnson-Lindenstrauss-Transform. Although JL often works well, it is the computational bottleneck of many applications, such as approximate nearest neighbor searching.24, 27 In such cases, substituting FJLT yields an immediate improvement. Another benefit is that implementing FJLT remains extremely simple. Later in Section 3 we show how FJLT helps in some of the applications mentioned above. Until then, we concentrate on the story of FJLT itself, which is interesting in its own right.
 1.1. A brief history of a quest for a faster
JL
1.1. A brief history of a quest for a faster
JL
Before describing our result, we present the original JL result in detail, as well as survey results related to its computational aspects. We begin with the central lemma behind JL.25 The following are the main variables we will be manipulating:
X—a set of vectors in Euclidean space (our input data-set). In what follows, we use the term points and vectors interchangeably.
n—the size of the set X.
d—the dimension of the Euclidean space (typically very big).
k—the dimension of the space we will reduce the points in X to (ideally, much smaller than d).
ε—a small tolerance parameter, measuring to what is the maximum allowed distortion rate of the metric space induced by the set X in Euclidean m-space (the exact definition of distortion will be given below).
In JL, we take k to be cε−2 log n, for some large enough absolute constant c. We then choose a random subspace of dimension k in Rd (we omit the mathematical details of what a random subspace is), and define Φ to be the operation of projecting a point in Rd onto the subspace. We remind the reader that such an operation is linear, and is hence equivalently representable by a matrix. In other words, we've just defined a random matrix. Denote it by Φ.
The JL Lemma states that with high probability, for all pairs
of points x, y 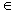 X simultaneously,
X simultaneously,
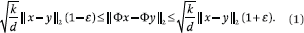
This fact is useful provided that k < d, which will be implied by the assumption

Informally, JL says that projecting the n points on a
random low-dimensional subspace should, up to a distortion
of 1 ± ε, preserve pairwise distances. The
mapping matrix of size Φ = k × d can be
implemented in a computer program as follows: The first row is a
random unit vector chosen uniformly in
Rd; the second row is a random unit
vector from the space orthogonal to the first row; the third is a
random unit vector from the space orthogonal to the first two
rows, etc. The high-level proof idea is to show that for each
pair x, y 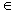 X the probability of (1) being
violated is order of 1/n2. A standard union
bound over the number of pairs of points in X then
concludes the proof.
X the probability of (1) being
violated is order of 1/n2. A standard union
bound over the number of pairs of points in X then
concludes the proof.
It is interesting to pause and ask whether the JL theorem
should be intuitive. The answer is both yes and no.
Low-dimensional geometric intuition is of little help. Take an
equilateral triangle ABC in the plane (Figure 2),
no matter how you project it into a line, you get three points in
a row, two of which form a distance at least twice the smallest
one. The distortion is at least 2, which is quite bad. The
problem is that, although the expected length of each side's
projection is identical, the variance is high. In other words,
the projected distance is rarely close to the average. If,
instead of d = 2, we choose a high dimension d and
project down to k = cε−2
log n dimensions, the three projected lengths of ABC still
have the same expected value, but crucially their (identical)
variances are now very small. Why? Each such length (squared) is
a sum of k independent random variables, so its
distribution is almost normal with variance proportional to
k (this is a simple case of the central limit theorem).
This fact alone explains each factor in the expression for
k: ε−2 ensures the desired
distortion; log n reduces the error probability to
n−c', for constant c'
growing with c, which allows us to apply a union bound
over all  pairs of distances in X.
pairs of distances in X.
Following Johnson and Lindenstrauss,25 various researchers suggested simplifications of the original JL design and of their proofs (Frankl and Maehara,20 DasGupta and Gupta,17 Indyk and Motwany24). These simplifications slightly change the distribution from which Φ is drawn and result in a better constant c and simpler proofs. These results, however, do not depart from the original JL from a computational point of view, because the necessary time to apply Φ to a vector is still order of nk.
A bold and ingenious attempt to reduce this cost was taken by
Achlioptas.1 He noticed that the only
property of Φ needed for the transformation to work is that
(Φi · x)2 be
tightly concentrated around the mean 1/d for all unit
vectors x 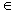 Rd, where
Φi is the ith row of Φ. The
distribution he proposed is very simple: Choose each element of
Φ uniformly from the following distribution:
Rd, where
Φi is the ith row of Φ. The
distribution he proposed is very simple: Choose each element of
Φ uniformly from the following distribution:
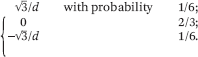
The nice property of this distribution is that it is relatively sparse: on average, a fraction 2/3 of the entries of Φ are 0. Assuming we want to apply Φ on many points in Rd in a real-time setting, we can keep a linked list of all the nonzeros of Φ during preprocessing and reap the rewards in the form of a threefold speedup in running time.
Is Achlioptas's result optimal, or is it possible to get a super constant speedup? This question is the point of departure for this work. One idea to obtain a speedup, aside from sparsifying Φ, would be to reduce the target dimension k, and multiply by a smaller matrix Φ. Does this have a chance of working? A lower bound of Alon5 provides a negative answer to this question, and dashes any hope of reducing the number of rows of Φ by more than a factor of O(log(1/ε)). The remaining question is hence whether the matrix can be made sparser than Achlioptas's construction. This idea has been explored by Bingham and Mannila.11 They considered sparse projection heuristics, namely, fixing most of the entries of Φ as zeroes. They noticed that in practice such matrices Φ seem to give a considerable speedup with little compromise in distortion for data found in certain applications. Unfortunately, it can be shown that sparsifying Φ by more than a constant factor (as implicitly suggested in Bingham and Mannila's work) will not work for all inputs. Indeed, a sparse matrix will typically distort a sparse vector. The intuition for this is given by an extreme case: If both Φ and the vector x are very sparse, the product Φx may be null, not necessarily because of cancellations, but more simply because each multiplication Φijxj is itself zero.
 1.2. The random densification technique
1.2. The random densification technique
In order to prevent the problem of simultaneous sparsity of Φ and x, we use a central concept from harmonic analysis known as the Heisenberg principle—so named because it is the key idea behind the Uncertainty Principle: a signal and its spectrum cannot be both concentrated. The look of frustration on the face of any musician who has to wrestle with the delay from a digital synthesizer can be attributed to the Uncertainty Principle.
Before we show how to use this principle, we must stop and ask: what are the tools we have at our disposal? We may write the matrix Φ as a product of matrices, or, algorithmically, apply a chain of linear mappings on an input vector. With that in mind, an interesting family of matrices we can apply to an input vector is the orthogonal family of d-by-d matrices. Such matrices are isometries: The Euclidean geometry suffers no distortion from their application.
With this in mind, we precondition the random k-by-d mapping with a Fourier transform (via an efficient FFT algorithm) in order to isometrically densify any sparse vector. To prevent the inverse effect, i.e., the sparsification of dense vectors, we add a little randomization to the Fourier transform (see Section 2 for details). The reason this works is because sparse vectors are rare within the space of all vectors. Think of them as forming a tiny ball within a huge one: if you are inside the tiny ball, a random transformation is likely to take you outside; on the other hand, if you are outside to begin with, the transformation is highly unlikely to take you inside the tiny ball.
The resulting FJLT shares the low-distortion characteristics of JL but with a lower running time complexity.
2. The Details of FJLT
In this section we show how to construct a matrix Φ drawn from FJLT and then prove that it works, namely:
- It provides a low distortion guarantee. (In addition to
showing that it embeds vectors in low-dimensional
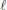 k2, we will show it also embeds
in
k2, we will show it also embeds
in 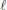 k1.)
k1.) - Applying it to a vector is efficiently computable.
The first property is shared by the standard JL and its variants, while the second one is the main novelty of this work.
 2.1. Constructing Φ
2.1. Constructing Φ
We first make some simplifying assumptions. We may assume with no loss of generality that d is a power of two, d = 2h > k, and that n Ω d = Ω(ε−1/2); otherwise the dimension of the reduced space is linear in the original dimension. Our random embedding Φ ~ FJLT (n, d, ε, p) is a product of three real-valued matrices (Figure 3):
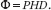
The matrices P and D are chosen randomly whereas H is deterministic:
- P is a k-by-d matrix. Each element is an independent mixture of 0 with an unbiased normal distribution of variance 1/q, where
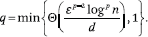
- In other words, Pij ~ N(0, 1/q) with probability q, and Pij = 0 with probability 1 - q.
- H is a d-by-d normalized Walsh-Hadamard matrix:
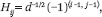
- where 〈i, j〉 is the dot-product (modulo 2) of the m-bit vectors i,j expressed in binary.
- D is a d-by-d diagonal matrix, where each Dii is drawn independently from {-1, 1} with probability 1/2.
The Walsh-Hadamard matrix corresponds to the discrete Fourier
transform over the additive group GF (2)d: its
FFT is very simple to compute and requires only O(d
log d) steps. It follows that the mapping Φx of
any point x  Rd can be
computed in time O(d log d + |P|),
where |P| is the number of nonzero entries in P.
The latter is O(ε−2 log n)
not only on average but also with high probability. Thus we can
assume that the running time of O(d log d +
qdε−2 log n) is
worst-case, and not just expected.
Rd can be
computed in time O(d log d + |P|),
where |P| is the number of nonzero entries in P.
The latter is O(ε−2 log n)
not only on average but also with high probability. Thus we can
assume that the running time of O(d log d +
qdε−2 log n) is
worst-case, and not just expected.
The FJLT Lemma. Given a fixed set X of n points
in Rd, ε < 1, and
p  {1, 2}, draw a matrix Φ from FJLT.
With probability at least 2/3, the following two events
occur:
{1, 2}, draw a matrix Φ from FJLT.
With probability at least 2/3, the following two events
occur:
- For any x
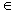 X,
X, 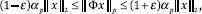 where
α1 =
where
α1 = 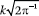 and α2 =
k.
and α2 =
k. - The mapping Φ Rd →
Rk requires
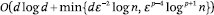 operations.
operations.
Remark: By repeating the construction O(log (1/δ)) times we can ensure that the probability of failure drops to δ for any desired δ > 0. By failure we mean that either the first or the second part of the lemma does not hold.
 2.2. Showing that Φ works
2.2. Showing that Φ works
We sketch a proof of the FJLT Lemma. Without loss of
generality, we can assume that ε <
ε0 for some suitably small
ε0. Fix x 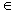 X. The
inequalities of the lemma are invariant under scaling, so we can
assume that ||x||2 = 1. Consider the random
variable u = HDx, denoted by (u1,
..., ud)T. The first
coordinate u1 is of the form
Σdi=1aixi,
where each ai = ±
d−1/2 is chosen independently and
uniformly. We can use a standard tail estimate technique to prove
that, with probability at least, say, 0.95,
X. The
inequalities of the lemma are invariant under scaling, so we can
assume that ||x||2 = 1. Consider the random
variable u = HDx, denoted by (u1,
..., ud)T. The first
coordinate u1 is of the form
Σdi=1aixi,
where each ai = ±
d−1/2 is chosen independently and
uniformly. We can use a standard tail estimate technique to prove
that, with probability at least, say, 0.95,
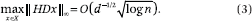
It is important to intuitively understand what (3) means.
Bounding  HDx
HDx ∞ is tantamount to
bounding the magnitude of all coordinates of HDx. This can
be directly translated to a densification property. To see
why, consider an extreme case: If we knew that, say,
∞ is tantamount to
bounding the magnitude of all coordinates of HDx. This can
be directly translated to a densification property. To see
why, consider an extreme case: If we knew that, say,
 HDx
HDx ∞ < 1, then we would
automatically steer clear of the sparsest case possible, in which
x is null in all but one coordinate (which would have to
be 1 by the assumption
∞ < 1, then we would
automatically steer clear of the sparsest case possible, in which
x is null in all but one coordinate (which would have to
be 1 by the assumption  x
x 2 =
2 =
 HDx
HDx 2 = 1).
2 = 1).
To prove (3), we first make the following technical observation:
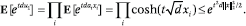
Setting t = sd above, we now use the technical observation together with Markov's inequality to conclude that, for any s > 0,
for 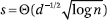 . A union bound over all nd ≥
n2 coordinates of the vectors
{HDx|x ε X} leads to (3). We assume
from now on that (3) holds with s as the upper bound; in
other words,
. A union bound over all nd ≥
n2 coordinates of the vectors
{HDx|x ε X} leads to (3). We assume
from now on that (3) holds with s as the upper bound; in
other words,  u
u ∞
∞ 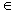 s,
where u = HDx. Assume now that u is fixed.
It is convenient (and immaterial) to choose s so that
mdef s−2 is an
integer.
s,
where u = HDx. Assume now that u is fixed.
It is convenient (and immaterial) to choose s so that
mdef s−2 is an
integer.
It can be shown that  u
u 2 =
2 =
 x
x 2 by virtue of both H
and D (and their composition) being isometries (i.e.,
preserve
2 by virtue of both H
and D (and their composition) being isometries (i.e.,
preserve  2 norms). Now define,
2 norms). Now define,
The vector y is the final mapping of x using Φ. It is useful to consider each coordinate of y separately. All coordinates share the same distribution (though not as independent random variables). Consider y1. By definition of FJLT, it is obtained as follows: Pick random i.i.d. indicator variables b1,..., bd, where each bj equals 1 with probability q; then draw random i.i.d. variables r1,..., rd from N(0, 1/q). Set y1 = Σdj=1 rjbjuj and let Z = Σdj=1 bj u2j. It can be shown that the conditional variable (y1|Z = z) is distributed N (0, z/q) (this follows a well known fact known as the 2-stability of the normal distribution). Note that all of y1,..., yk are i.i.d. (given u), and we can similarly define corresponding random i.i.d. variables Z1(= Z), Z2,..., Zk. It now follows that the expectation of Z satisfies:
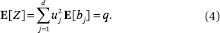
Let u2 formally denote
(u21, ...,
u2d) 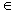 (R+)d. By our assumption that
(3) holds, u2 lies in the d-dimensional
polytope:
(R+)d. By our assumption that
(3) holds, u2 lies in the d-dimensional
polytope:
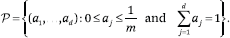
Let u* 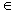 Rd denote a
vector such that u*2 is a vertex of
Rd denote a
vector such that u*2 is a vertex of
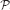 . By symmetry of these vertices, there will be no
loss of generality in what follows if we fix:
. By symmetry of these vertices, there will be no
loss of generality in what follows if we fix:
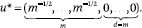
The vector u* will be convenient for identifying extremal cases in the analysis of Z. By extremal we mean the most problematic case, namely, the sparsest possible under assumption (3) (recall that the whole objective of HD was to alleviate sparseness).
We shall use Z* to denote the random variable Z corresponding to the case u = u*. We observe that Z* ~ m−1B(m, q); in words, the binomial distribution with parameters m, q divided by the constant m. Consequently,
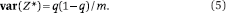
In what follows, we divide our discussion between the
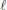 1 and the
1 and the 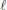 2 cases.
2 cases.
The 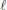 1 case: We choose
1 case: We choose
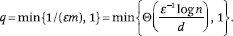
We now bound the moments of Z over the random bj's. LEMMA 1. For any t > 1, E[Zt] = O(qt)t, and
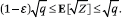
Proof: The case q = 1 is trivial because
Z is constant and equal to 1. So we assume q =
1/(εm) < 1. It is easy to verify that
E[Zt] is a convex function of
u2, and hence achieves its maximum at a vertex
of 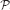 . So it suffices to prove the moment upper bounds
for Z*, which conveniently behaves like a (scaled)
binomial. By standard bounds on the binomial moments,
. So it suffices to prove the moment upper bounds
for Z*, which conveniently behaves like a (scaled)
binomial. By standard bounds on the binomial moments,
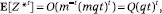
proving the first part of the lemma.
By Jensen's inequality and (4),
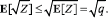
This proves the upper-bound side of the second part of the
lemma. To prove the lower-bound side, we notice that
E[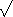 Z] is a concave function of
u2, and hence achieves its minimum when
u = u*. So it suffices to prove the desired lower
bound for
Z] is a concave function of
u2, and hence achieves its minimum when
u = u*. So it suffices to prove the desired lower
bound for 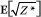 . Since
. Since 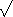 x ≥ 1 + 1/2
(x −1) - (x −1)2 for all
x ≥ 0,
x ≥ 1 + 1/2
(x −1) - (x −1)2 for all
x ≥ 0,
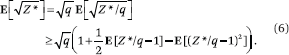
By (4), E[Z*/q −1] = 0 and, using (5),
Plugging this into (6) shows that 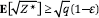 , as
desired.
, as
desired.
Since the expectation of the absolute value of N(0, 1)
is 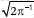 , by taking conditional expectations, we find
that
, by taking conditional expectations, we find
that
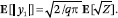
On the other hand, by Lemma 1, we note that
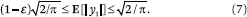
Next, we prove that  y
y 1 is
sharply concentrated around its mean
E[
1 is
sharply concentrated around its mean
E[ y
y 1] =
kE[|y1|]. To do this, we begin by
bounding the moments of |y1| =
|Σj bj
rj uj|. Using
conditional expectations, we can show that, for any integer
t ≥ 0,
1] =
kE[|y1|]. To do this, we begin by
bounding the moments of |y1| =
|Σj bj
rj uj|. Using
conditional expectations, we can show that, for any integer
t ≥ 0,
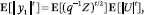
where U ~ N(0,1). It is well known that E[|U|t] = (t)t/2; and so, by Lemma 1,
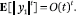
It follows that the moment generating function satisfies
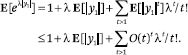
Therefore, it converges for any 0 ≤ λ < λ0, where λ0 is an absolute constant, and
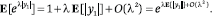
Using independence, we find that
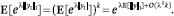
Meanwhile, Markov's inequality and (7) imply that
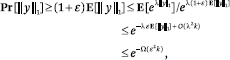
for some λ = Θ (ε). The constraint
λ < λ0 corresponds to ε being
smaller than some absolute constant. The same argument leads to a
similar lower tail estimate. Our choice of k ensures that,
for any x 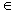 X,
X,  Φx
Φx 1
=
1
=  y
y 1 deviates from its mean by
at most ε with probability at least 0.95. By (7), this
implies that kE[|y1|] is itself
concentrated around
1 deviates from its mean by
at most ε with probability at least 0.95. By (7), this
implies that kE[|y1|] is itself
concentrated around  with a relative error at most
ε; rescaling ε by a constant factor and ensuring
(3) proves the
with a relative error at most
ε; rescaling ε by a constant factor and ensuring
(3) proves the 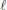 1 claim of the first part of the
FJLT lemma.
1 claim of the first part of the
FJLT lemma.
The 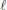 2 case: We set
2 case: We set
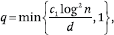
for a large enough constant c1.
LEMMA 2. With probability at least 1-1/20n'
- q/2 ≤ Zi ≤ 2q for all i = 1,..., k; and
- kq(1 - ε) ≤ Σki=1 Zi ≤ kq(1 + ε).
Proof: If q = 1 then Z is the constant q and the claim is trivial. Otherwise, q = c1 d−1 log2 n < 1. For any real λ, the function
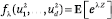
is convex, hence achieves its maximum at the vertices of the
polytope  (same as in the proof of Lemma 1). As
argued before, therefore,
E[eλZ] ≤
E[eλZ*]. We conclude the
proof of the first part with a union bound on standard tail
estimates on the scaled binomial Z* that we derive from
bounds on its moment generating function
E[eλZ*] (e.g., Alon and
Spencer6). For the second part, let
S = Σki=1
Zi. Again, the moment generating
function of S is bounded above by that of S* ~
m−1 B(mk,
q)—all Zi's are distributed
as Z*—and the desired concentration bound
follows.
(same as in the proof of Lemma 1). As
argued before, therefore,
E[eλZ] ≤
E[eλZ*]. We conclude the
proof of the first part with a union bound on standard tail
estimates on the scaled binomial Z* that we derive from
bounds on its moment generating function
E[eλZ*] (e.g., Alon and
Spencer6). For the second part, let
S = Σki=1
Zi. Again, the moment generating
function of S is bounded above by that of S* ~
m−1 B(mk,
q)—all Zi's are distributed
as Z*—and the desired concentration bound
follows.
We assume from now on that the premise of Lemma 2 holds for
all choices of x  X. A union bound shows that
this happens with probability of at least 0.95. For each i
= 1, ..., k the random variable
y2i
q/Zi is distributed as
λ2 with one degree of freedom. It follows that,
conditioned on Zi; the expected value of
y2i is
Zi/q and the moment generating
function of y2i is
X. A union bound shows that
this happens with probability of at least 0.95. For each i
= 1, ..., k the random variable
y2i
q/Zi is distributed as
λ2 with one degree of freedom. It follows that,
conditioned on Zi; the expected value of
y2i is
Zi/q and the moment generating
function of y2i is
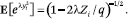
Given any 0 < λ < λ0, for fixed λ0, for large enough ξ, the moment generating function converges and is equal to
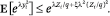
We use here the fact that Zi/q = O(1), which we derive from the first part of Lemma 2. By independence, therefore,
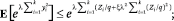
and hence
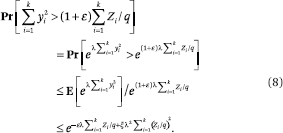
If we plug
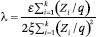
into (8) and assume that ε is smaller than some global ε0, we avoid convergence issues (Lemma 2). By that same lemma, we now conclude that
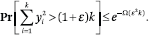
A similar technique can be used to bound the left tail
estimate. We set k = cε−2
log n for some large enough c and use a union
bound, possibly rescaling ε, to conclude the
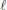 2 case of the first part of the FJLT lemma.
2 case of the first part of the FJLT lemma.
Running Time: The vector Dx requires O(d) steps, since D is diagonal. Computing H(Dx) takes O(d log d) time using the FFT for Walsh-Hadamard. Finally, computing P(H Dx) requires O(|P|) time, where |P| is the number of nonzeros in P. This number is distributed in B(nk, q). It is now immediate to verify that
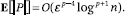
A Markov bound establishes the desired complexity of the FJLT. This concludes our sketch of the proof of the FJLT lemma.
3. Applications
 3.1. Approximate nearest neighbor
searching
3.1. Approximate nearest neighbor
searching
Given a metric space (U, dU)
and a finite subset (database) P  U, the
problem of ε-approximate nearest neighbor
(ε-ANN) searching is to preprocess P so that,
given a query x
U, the
problem of ε-approximate nearest neighbor
(ε-ANN) searching is to preprocess P so that,
given a query x 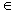 U, a point p
U, a point p 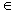 P satisfying
P satisfying
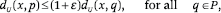
can be found efficiently. In other words, we are interested in a point p further from x by a factor at most (1 + ε) of the distance to its nearest neighbor.
This problem has received considerable attention. There are two good reasons for this: (i) ANN boasts more applications than virtually any other geometric problem23; (ii) allowing a small error ε makes it possible to break the curse of dimensionality.24, 27
There is abundant literature on (approximate) nearest neighbor searching.8, 9, 10, 12, 13, 15, 16, 19, 21, 22, 23, 24, 26, 27, 33, 39, 40 The early solutions typically suffered from the curse of dimensionality, but the last decade has witnessed a flurry of new algorithms that "break the curse" (see Indyk23 for a recent survey).
The first algorithms with query times of poly(d, log n) and polynomial storage (for fixed ε) were those of Indyk and Motwani24 in the Euclidean space case, and Kushilevitz et al.27 in the Hamming cube case. Using JL, Indyk et al. provide a query time of O(ε−2d log n) with nO(ε −2) storage and preprocessing. A discrete variant of JL was used by Kushilevitz et al. in the Hamming cube case. We mention here that the dimension reduction overwhelms the running time of the two algorithms. In order to improve the running time in both cases, we used two main ideas in Ailon and Chazelle.2 The first idea applied to the discrete case. It used an observation related to the algebraic structure of the discrete version of JL used in Kushilevitz et al.27 to obtain a speedup in running time. This observation was only applicable in the discrete case, but suggested the intuitive idea that a faster JL should be possible in Euclidean space as well, thereby motivating the search for FJLT. Indeed, by a straightforward application in Indyk et al.'s algorithm (with p = 1), the running time would later be improved using FJLT to O(d log d + ε−3 log2 n). Notice the additive form of this last expression in some function f = f (d) and g = g(n, ε), instead of a multiplicative one.
 3.2. Fast approximation of large
matrices
3.2. Fast approximation of large
matrices
Large matrices appear in virtually every corner of science. Exact algorithms for decomposing or solving for large matrices are often inhibitively expensive to perform. This may change given improvements in matrix multiplication technology, but it appears that we will have to rely on matrix approximation strategies for a while, at least in the general case. It turns out that FJLT and ideas inspired by it play an important role in recent developments.
We elaborate on an example from a recent solution of
Sarlós36 to the problem of
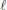 2 regression (least square fit of an
overdetermined linear system). Prior to that work (and ours),
Drineas et al.18 showed that, by
downsampling (choosing only a small subset and discarding the
rest) from the set of equations of the linear regression, an
approximate solution to the problem could be obtained by solving
the downsampled problem, the size of which depends only on the
dimension d of the original solution space. The difficulty
with this method is that the downsampling distribution depends on
norms of rows of the left-singular vector matrix of the original
system. Computing this matrix is as hard as the original
regression problem and requires O
(m2d) operations, with m the
number of equations. To make this solution more practical,
Sarlós observed that multiplying the equation matrix on
the left by the m × m orthogonal matrix
HD (as defined above in the definition of FJLT) implicitly
multiplies the left-singular vectors by HD as well. By an
analysis similar to the one above, the resulting left-singular
matrix can be shown to have almost uniform row norm. This allows
use of Drineas et al.'s ideas with uniform sampling of the
equations. Put together, these results imply the first
o(m2d) running time solution for
worst-case approximate
2 regression (least square fit of an
overdetermined linear system). Prior to that work (and ours),
Drineas et al.18 showed that, by
downsampling (choosing only a small subset and discarding the
rest) from the set of equations of the linear regression, an
approximate solution to the problem could be obtained by solving
the downsampled problem, the size of which depends only on the
dimension d of the original solution space. The difficulty
with this method is that the downsampling distribution depends on
norms of rows of the left-singular vector matrix of the original
system. Computing this matrix is as hard as the original
regression problem and requires O
(m2d) operations, with m the
number of equations. To make this solution more practical,
Sarlós observed that multiplying the equation matrix on
the left by the m × m orthogonal matrix
HD (as defined above in the definition of FJLT) implicitly
multiplies the left-singular vectors by HD as well. By an
analysis similar to the one above, the resulting left-singular
matrix can be shown to have almost uniform row norm. This allows
use of Drineas et al.'s ideas with uniform sampling of the
equations. Put together, these results imply the first
o(m2d) running time solution for
worst-case approximate 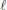 2 regression.
2 regression.
In a recent stream of papers, authors Liberty, Martinsson, Rokhlin, Tygert and Woolfe28, 35, 38 design and analyze fast algorithms for low-dimensional approximation algorithms of matrices, and demonstrate their application to the evaluation of the SVD of numerically low-rank matrices. Their schemes are based on randomized transformations akin to FJLT.
4. Beyond FJLT
The FJLT result gives rise to the following question: What is a lower bound, as a function of n, d and ε, on the complexity of computing a JL-like random linear mapping? By this we mean a mapping that distorts pairwise Euclidean distances among any set of n points in d dimension by at most 1 ± ε. The underlying model of computation can be chosen as a linear circuit,32 manipulating complex-valued intermediates by either adding two or multiplying one by (random) constants, and designating n as input and k = O(ε−2 log n) as output (say, for p = 2). It is worth observing that any lower bound in Ω(ε−2 log n min{d, log2 n}) would imply a similar lower bound on the complexity of computing a Fourier transform. Such bounds are known only in a very restricted model31 where constants are of bounded magnitude.
As a particular case of interest, we note that, whenever k = O(d1/3), the running time of FJLT is O(d log d). In a more recent paper, Ailon and Liberty3 improved this bound and showed that it is possible to obtain a JL-like random mapping in time O(d log d) for k = O(d1/2 - δ) and any δ > 0. Their transformation borrows the idea of preconditioning a Fourier transform with a random diagonal matrix from FJLT, but uses it differently and takes advantage of stronger measure concentration bounds and tools from error correcting codes over fields of characteristic 2. The same authors together with Singer consider the following inverse problem4: Design randomized linear time computable transformations that require the mildest assumptions possible on data to ensure successful dimensionality reduction.
References
1. Achlioptas, D. Database-friendly random projections: Johnson–Lindenstrauss with binary coins. J. Comput. Syst. Sci. 66, 4 (2003), 671–687.
2. Ailon, N., Chazelle, B. Approximate nearest neighbors and the fast Johnson-Lindenstrauss transform. SIAM J. Comput. 39, 1 (2009), 302–322.
3. Ailon, N., Liberty, E. Fast dimension reduction using rademacher series on dual bch codes. Discrete and Computational Geometry (2008).
4. Ailon, N., Liberty, E., Singer, A. Dense fast random projections and lean walsh transforms. APPROX-RANDOM, 2008, 512–522.
5. Alon, N. Problems and results in extremal combinatorics-I. Discrete Math. 273, 1–3 (2003), 31–53.
6. Alon, N., Spencer, J. The Probabilistic Method. John Wiley, 2nd edition, 2000.
7. Arora, S. Polynomial time approximation schemes for euclidean traveling salesman and other geometric problems. J. ACM 45, 5 (1998), 753–782.
8. Arya, S., Mount, D.M. Approximate nearest neighbor queries in fixed dimensions. In Proceedings of the 4th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA) (Austin, TX, United States, 1993), 271–280.
9. Arya, S., Mount, D.M., Netanyahu, N.S., Silverman, R., Wu, A.Y. An optimal algorithm for approximate nearest neighbor searching fixed dimensions. J. ACM 45, 6 (1998), 891–923.
10. Bern, M.W. Approximate closest-point queries in high dimensions. Inf. Process. Lett. 45, 2 (1993), 95–99.
11. Bingham, E., Mannila, H. Random projection in dimensionality reduction: Applications to image and text data. In Knowledge Discovery and Data Mining, 2001, 245–250.
12. Borodin, A., Ostrovsky, R., Rabani, Y. Lower bounds for high dimensional nearest neighbor search and related problems. In Proceedings of the 31st Annual Symposium on the Theory of Computing (STOC) (1999), 312–321.
13. Chan, T.M. Approximate nearest neighbor queries revisited. Discrete Comput. Geometry 20, 3 (1998), 359–373.
14. Christofides, N. Worst-case analysis of a new heuristic for the travelling salesman problem. Technical Report, Graduate School of Industrial Administration, Carnegie-Mellon University, Pittsburgh, 1976, 388.
15. Clarkson, K.L. An algorithm for approximate closest-point queries. In Proceedings of the 10th Annual ACM Symposium on Computational Geometry (SoCG) (1994), 160–164.
16. Clarkson, K.L. Nearest neighbor queries in metric spaces. Discrete Comput. Geometry 22, 1 (1999), 63–93.
17. DasGupta, S., Gupta, A. An elementary proof of the Johnson–Lindenstrauss lemma. Technical Report, UC Berkeley, 1999, 99–106.
18. Drineas, P., Mahoney, M.W.,
Muthukrishnan, S. Sampling algorithms for  2
regression and applications. In Proceedings of the 17th Annual
ACM-SIAM Symposium on Discrete Algorithms (SODA) (Miami, FL,
United States, 2006).
2
regression and applications. In Proceedings of the 17th Annual
ACM-SIAM Symposium on Discrete Algorithms (SODA) (Miami, FL,
United States, 2006).
19. Farach-Colton, M., Indyk, P. Approximate nearest neighbor algorithms for Hausdorff metrics via embeddings. In Proceedings of the 40th Annual IEEE Symposium on Foundations of Computer Science (FOCS) (1999), 171–180.
20. Frankl, P., Maehara, H. The Johnson–Lindenstrauss lemma and the sphericity of some graphs. J. Comb. Theory Ser. A 44 (1987), 355–362.
21. Indyk, P. On approximate nearest neighbors in non-Euclidean spaces. In Proceedings of the 39th Annual IEEE Symposium on Foundations of Computer Science (FOCS) (1998), 148–155.
22. Indyk, P. Dimensionality reduction techniques for proximity problems. In Proceedings of the 11th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA) (2000), 371–378.
23. Indyk, P. Nearest neighbors in high-dimensional spaces. In Handbook of Discrete and Computational Geometry. CRC, 2004.
24. Indyk P., Motwani, R. Approximate nearest neighbors: Towards removing the curse of dimensionality. In Proceedings of the 30th Annual ACM Symposium on Theory of Computing (STOC) (1998), 604–613.
25. Johnson, W.B., Lindenstrauss, J. Extensions of Lipschitz mappings into a Hilbert space. Contemp. Math. 26 (1984), 189–206.
26. Kleinberg, J.M. Two algorithms for nearest-neighbor search in high dimensions. In Proceedings of the 29th Annual ACM Symposium on Theory of Computing (STOC) (1997), 599–608.
27. Kushilevitz, E., Ostrovsky, R., Rabani Y. Efficient search for approximate nearest neighbor in high dimensional spaces. SIAM J. Comput. 30, 2 (2000), 457–474.
28. Liberty, E., Woolfe, F., Martinsson, P.-G., Rokhlin, V., Tygert, M. Randomized algorithms for the low-rank approximation of matrices. Proc. Natl. Acad. Sci. (PNAS) 104, 51 (2007), 20167–20172.
29. Linial, N., London, E., Rabinovich, Y. The geometry of graphs and some of its algorithmic applications. Combinatorica 15, 2 (1995), 215–245.
30. Mitchell, J.S.B. Guillotine subdivisions approximate polygonal subdivisions: A simple new method for the geometric k-MST problem. SIAM J. Comput. 28, 4 (1999), 1298–1309.
31. Morgenstern, J. Note on a lower bound on the linear complexity of the fast fourier transform. J. ACM 20, 2 (1973), 305–306.
32. Morgenstern, J. The linear complexity of computation. J. ACM 22, 2 (1975), 184–194.
33. Muthukrishnan, S., Sahinalp, S.C. Simple and practical sequence nearest neighbors with block operations. In Proceedings of the 13th Annual Symposium on Combinatorial Pattern Matching (CPM) (2002), 262–278.
34. Papadimitriou, C., Raghavan, P., Tamaki, H., Vempala, S. Latent semantic indexing: A probabilistic analysis. In Proceedings of the 17th Annual Symposium of Database Systems (1998), 159–168.
35. Rokhlin, V., Tygert, M. A fast randomized algorithm for overdetermined linear least-squares regression. Proceedings of the National Academy of Science (PNAS) 105, 36 (2008), 13212–13217.
36. Sarlós, T. Improved approximation algorithms for large matrices via random projections. In Proceedings of the 47th Annual IEEE Symposium on Foundations of Computer Science (FOCS) (Berkeley, CA, 2006).
37. Schulman, L. Clustering for edge-cost minimization. In Proceedings of the 32nd Annual Symposium on Theory of Computing (STOC) (2000), 547–555.
38. Woolfe, F., Liberty, E., Rokhlin, V., Tygert, M. A fast randomized algorithm for the approximation of matrices. Appl. Comput. Harmon. Anal. 25 (2008), 335–366.
39. Yianilos, P.N. Data structures and algorithms for nearest neighbor search in general metric spaces. In Proceedings of the 4th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA) (1993), 311–321.
40. Yianilos, P.N. Locally lifting the curse of dimensionality for nearest neighbor search (extended abstract). In Proceedings of the 11th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA) (2000), 361–370.
Footnotes
A previous version of this paper appeared in Proceedings of the 38th ACM Symposium on Theory in Computing (May 2006, Seattle, WA).
DOI: https://doi.acm.org/10.1145/1646353.1646379
Figures
 Figure 1. Embedding a spherical metric onto a planar one
is no easy task. The latter is more favorable as input to
printers.
Figure 1. Embedding a spherical metric onto a planar one
is no easy task. The latter is more favorable as input to
printers.
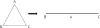 Figure 2. A triangle cannot be embedded onto a line
while simultaneously preserving distances between all pairs of
vertices.
Figure 2. A triangle cannot be embedded onto a line
while simultaneously preserving distances between all pairs of
vertices.
©2010 ACM 0001-0782/10/0200 $10.00
Permission to make digital or hard copies of all or part of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. To copy otherwise, to republish, to post on servers or to redistribute to lists, requires prior specific permission and/or a fee.
The Digital Library is published by the Association for Computing Machinery. Copyright © 2010 ACM, Inc.
Sign In To Comment On This Article
sign in
get access
Create a Web Account
If you are already an ACM member, Communications subscriber, or Digital Library subscriber, please set up a web account to access premium content on this site.
Join the ACM 
Become a member to view this article and take full advantage of ACM's outstanding computing information resources, networking opportunities, and other benefits.
Subscribe to Communications of the ACM
Get full access to 50+ years of CACM content and receive the print version of the magazine monthly.
Tools For Readers
Related ACM Resources
Conferences:
- GRAPP 2011: International Conference on Computer Graphics Theory and Applications
 - March 5 – 7, 2011; Algarve, Portugal
- March 5 – 7, 2011; Algarve, Portugal
Books:
- Mastering Enterprise JavaBeans, Third Edition
 - Ed Roman, Rima Patel Sriganesh and Gerald Brose
- Ed Roman, Rima Patel Sriganesh and Gerald Brose
Courses:
- VPN Design Fundamentals v2.0
 - In this course, you will describe various VPN technologies so that
you can create a VPN solution based on a customer's requirements. You
will identify …
- In this course, you will describe various VPN technologies so that
you can create a VPN solution based on a customer's requirements. You
will identify …




