Why Trisecting the Angle is Impossible
Steven Dutch, Natural and Applied Sciences, University
of Wisconsin - Green Bay
First-time Visitors: Please visit Site Map and Disclaimer.
Use "Back" to return here.
A Note to Visitors
I will respond to questions and comments as time permits, but if you want to take issue
with any position expressed here, you first have to answer this question:
What evidence would it take to prove your beliefs wrong?
I simply will not reply to challenges that do not address this question. Refutability
is one of the classic determinants of whether a theory can be called scientific. Moreover,
I have found it to be a great general-purpose cut-through-the-crap question to determine
whether somebody is interested in serious intellectual inquiry or just playing mind games.
It's easy to criticize science for being "closed-minded". Are you open-minded
enough to consider whether your ideas might be wrong?
The ancient Greeks founded Western mathematics, but as ingenious as they were, they
could not solve three problems:
It was not until the 19th century that mathematicians showed that these problems could
not be solved using the methods specified by the Greeks. Any good draftsman can
do all these constructions accurate to any desired limits of accuracy - but not to absolute
accuracy. The Greeks themselves invented ways to solve the first two exactly, using tools
other than a straightedge and compass. But under the conditions the Greeks specified, the
problems are impossible.
Since we can do these tasks to any desired accuracy already, there is no practical
use whatever for an exact geometrical solution of these problems. So if you think you'll
get headlines, endorsement contracts and dates with supermodels for doing so, it is my sad duty to tell you
otherwise.
Also, there are a few trivial special cases, like a right angle, where it is
possible to "trisect" the angle. More specifically, it is possible to construct an
angle one-third the given angle. For example, if you draw a diameter of a circle
and mark off 60 degree intervals on the circle, you "trisect" the
straight angle. This isn't trisection in any meaningful sense because it doesn't
generalize to other angles.
"Impossible" is a welcome challenge to a lot of people. The problems are so
easy to understand, but the impossibility proofs are so advanced, that many
people flatly refuse to accept the problems are impossible. I am not out to persuade these
people. Mathematicians have spent years corresponding with some of them, and many are
absolutely immune to persuasion (The trisectors, I mean. The mathematicians are too, but
they have reason to be). But if you want a (hopefully) intelligible explanation of why
mathematicians regard the problems as impossible - as proven to be impossible -
then this site might help you.
Warning: you need trigonometry and an understanding of polynomials -
that is, the equivalent of a good high school math education - to follow this discussion.
Proving Things Impossible
One of the major problems people have with angle trisection is the very idea that
something can be proven impossible. Many people flatly deny that anything can be
proven to be impossible. But isn't that a contradiction? If nothing can be proven to be
impossible, and you can prove it, then you've proven something to be impossible, and
contradicted yourself. In fact, showing that something entails a contradiction is a
powerful means of showing that some things are impossible. So before tackling the
trisection problem, let's spend some time proving a few things impossible just to show
that it can be done.
The Domino Problem
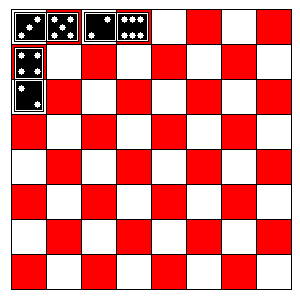 |
Imagine you have a checkerboard and start covering it with
dominoes so that each domino covers two squares. Obviously there are a
vast number of ways to do it. |
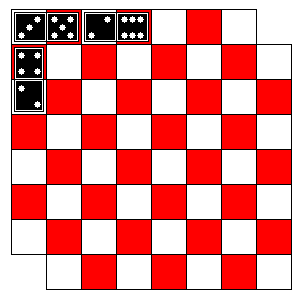 |
Now imagine you remove two opposite corner squares. Can you
still cover the checkerboard with dominoes?
No. Rather than try every possible way to place dominoes on the board,
consider this: each domino covers both a red and a white square. If you
remove the two corners shown, there will be 32 white squares but only 30
red squares. There's no way to cover the board with dominoes without
leaving two unpaired white squares. So it can't be done. We have proven
that something is impossible.
|
I expect some die-hard to ask what about coloring a white square red so there
are 31 of each color. It doesn't matter. (Actually, it's easy to see that
coloring a white square red will create a situation where you have to cover two
red squares with a domino. Once you cover them, you have an unequal number of
red and white squares remaining, and then we're back to square one, literally.) You can paint the board psychedelic if
you like and it still can't be done. The traditional checkerboard coloring makes
it easy to prove it, but if it can't be done on a traditional checkerboard
pattern, it can't be done, period. In fact, a lot of proofs depend on marking,
labeling, or grouping items in a certain way to show that some particular
arrangement either is, or is not, possible.
An Oldie but Goodie: The Largest Prime Number
Prime numbers like 2, 3, 5, 7, 11 .... are divisible only by themselves and one. As
numbers get bigger, primes get more rare. Is there a largest one?
The ancient Greeks showed there is not. Imagine there is a largest prime p. Now
calculate the number q, which is 2 x 3 x 5 x 7 x 11 x...(all the primes less than p) x p. It will be a huge number. Now
consider q+1. It's not divisible by 2, because q is divisible by 2. Likewise, it's not
divisible by 3, 5, 7, or any other prime up to p, because q is divisible by all those
numbers. So there are only two possibilities. Either q+1 is prime, or it's divisible by
primes bigger than p (q+1 will be vastly bigger than p - if p is only 19 than q is
9,699,690 - there's lots of room for bigger primes). Either way the initial assumption
leads to a contradiction. Hence it must be wrong. There is no largest prime. It is impossible
to find a largest prime. It's not that people have tried, failed, and given up. It's
impossible because the idea itself leads to a contradiction. This method of proof - making
an assumption and then showing that it leads to a contradiction - is called reductio
ad absurdum.
It is impossible to find a largest prime, but it is possible to find
arbitrarily long stretches of numbers without them. Our number q is composite -
it is the product of smaller numbers. It's easy to see that q+2 must be composite, as well
as q+3, q+4 (divisible by 2) q+5, q+6 (divisible by 2 and 3) and so on up to q+p. We can
find so-called "prime deserts" of any desired length, but
there are always primes after them. Indeed, we keep finding pairs of primes, like
5 and 7, or 101 and 103, however high we go, though nobody has yet shown there is an
infinite number of them.
Another Golden Oldie: Square Root of Two
Can you represent the square root of two as a fraction? The ancient Greeks also found
out that this is impossible. Imagine that there is a fraction p/q, where p and q are whole
numbers and p/q is in lowest terms (that qualifier is important), that equals the
square root of two. We can conclude:
- p2/q2 = 2 and therefore:
- p2 = 2q2, therefore,
- p is even, since p2 is even and only even numbers have even squares. Also,
- p2 is divisible by 4, since all even squares are divisible by 4. Thus 2q2
is divisible by 4 which means q2 must be divisible by 2. Therefore q must also
be even.
- Thus p and q must both be even. Since we assumed they were in lowest terms, and have
arrived at a contradiction, the assumption must be false. We have another reductio ad
absurdum. It is impossible to represent the square root of two as a fraction
of whole numbers.
The sect called the Pythagoreans believed that everything was ultimately based
on whole numbers. They were horrified by this discovery. Tradition has it that they
decreed death to any member who divulged the secret. They called numbers that could not be
represented as ratios as irrational, and to this day irrational carries
a negative connotation. Actually this proof is related to the proofs that trisecting the
angle, doubling the cube and squaring the circle are impossible.
Uniform Polyhedra
Reductio ad absurdum is a powerful way of showing that some things are
impossible, but not the only way. If we can succeed in showing all the things that are
possible, then anything else must be impossible.
In simple cases we can list the possibilities by brute force. For example,
what kinds of three dimensional shapes have regular polygon faces, with all
faces and vertices identical? Clearly you have to have at least three faces
meeting at a vertex, and the sum of all the angles meeting at a vertex can't
equal or exceed 360 degrees. For triangles, we can have three, four or five
meeting at a vertex (six would equal 360 degrees). For squares we can have only
three, same for pentagons, and for hexagons and above, it can't be done (three
hexagons add up to 360 degrees). So that's it. There are five shapes, and no
others, shown below. (If you allow faces and edges to cross through each other,
it gets a bit more interesting.)
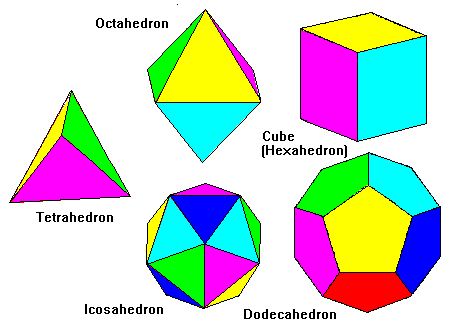
What Kinds of Plane Patterns are Possible?
When there are a potentially infinite number of possibilities, we
have to use
the general properties of the problem to devise a proof. Here's a
fairly simple example. What kinds of repeating patterns can we have on
a
plane, for example, wallpaper? We say something has n-fold symmetry if,
when you rotate it
360 degrees, there are n positions where it looks the same. For
example, a honeycomb has
six-fold symmetry - you can rotate it 360 degrees and there will be six
positions where
the pattern looks the same. A sheet of square graph paper has four-fold
symmetry. So does
a checkerboard if we ignore the colors, but if we include the colors,
then it only has
two-fold symmetry. Something with no symmetry at all has one-fold
symmetry.
| Now a single object like a flower or propeller can have any kind of
symmetry at all. But what about a pattern that repeats? Look at the pattern at
right. |
o o o v q o o
\ /
a\ /a
o o u-----x-----p o
o o o o o o o
|
The pattern consists of points, some of which are lettered. All the points are
identical (that's what a repeating pattern means). So if we can rotate the pattern around
one point and see symmetry, we can rotate it around every point. If we rotate the pattern
by angle a so it still looks the same, then a point originally at p will be rotated to the
same position as some other point (labeled q). Since we can rotate in either direction, a
point originally at u would be rotated in the other direction to some other point v. The
pattern shown here is the familiar honeycomb pattern, but notice we have not made any
assumptions about the angles in the pattern at all. The pattern shown is just for
illustration.
Let's assume each point is distance one from its neighbor: ux = xp = xv = xq = 1.
Distance vq has to be a whole number, but it need not be 1. If a = 90 degrees (4-fold
symmetry), it could be zero. But it has to be a whole number, because it's the distance
between two points on a row of the pattern. From elementary trigonometry, we can also see
that
vq = 2 cos a.
Now the cosine can only have values between -1 and 1, so 2 cos a, which must be a whole
number, can only take on values -2, -1, 0, 1 and 2. Thus cos a can only be -1, -1/2, 0,
1/2 and 1, or a = 180, 120, 90, 60 and 0 (or 360), respectively. Since the rotations are
symmetry rotations, a = 360/n, so n = 2, 3, 4, 6, or 1.
Thus, repeating patterns in the plane can only have 1, 2, 3, 4 or 6-fold symmetry.
In particular, repeating patterns in the plane cannot have five-fold symmetry.
- What about the stars in the flag? The stars have five-fold symmetry, but the
overall symmetry of the pattern does not. Rotate a flag by 72 degrees and see.
- In recent years some fascinating materials have turned up with five-fold symmetry. These
materials, termed quasicrystals, do not have repeating patterns. These are related
to beautiful patterns called Penrose Tilings,
which also have 5-fold symmetry but do not repeat regularly.
Notice, this is not a matter of people trying to find five-fold repeating patterns and
failing, then concluding it must be impossible. We devised a method to find all
the patterns that are possible. We showed that only certain patterns are possible;
therefore all the others are impossible. Many proofs of impossibility are based
on the fact that we show what is possible, thus ruling out everything else.
More (much more) on symmetry and patterns
What's With the Ruler and Compass Anyway?
Plato's famous analogy of the Cave gives a lot of insight into the Greek mathematical
mind. In this analogy, a prisoner in a cave knows the outside world only from shadows cast
on the wall of the cave. Needless to say, his knowledge of the world is pretty imperfect.
To many Greeks, this world, or at least our sensory picture of it, were crude images of a
perfect, real world. Thus, to Greek mathematicians, the lines we drew were crude
approximations of real lines, which were infinitely long, infinitely sharp,
infinitesimally narrow, and perfectly straight. In principle, lines intersected in
infinitely tiny, precise points. In geometry, "the truth is out there", the
answer already exists, and they sought constructions that would find the answer infallibly
and with infinite precision. Thus the Greeks rejected any technique that smacked of
approximation or trial and error. The problem with trial and error is that,
regardless how closely the construction seems to fit, we can never be sure there
isn't some microscopic error below the limits of our visibility. The Greeks wanted to find the correct point directly, the
first try, with absolute precision.
| It is possible to build tools that will solve the problem, using a ruler
and compass. One of the simplest, at right, was dubbed the "hatchet." It
consists of a right-angled T as shown with a semicircle on one side. Points A, B, C and D
are all equally spaced. Place A on one side of the angle with the long arm of the T
passing through O, and slide the hatchet so that the semicircle just touches the other
side of the angle at E. Lines OB and OC trisect the angle. The upper diagram
shows how it works, the lower diagram shows how one might be constructed
from cardboard. |
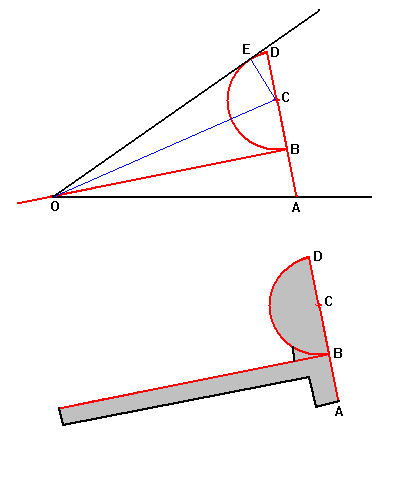 |
Proof: Since AB=BC and angles ABO and CBO are right angles, triangles AOB and
BOC are identical and angles AOB and BOC must be equal. Also BC=CE and angle CEO is a
right angle, so triangles BOC and COE are also identical and angles BOC and COE are
identical. Thus angle AOB = BOC = COE.
So what's wrong with this device? It can be laid out with ruler and compass,
but not physically made. A real hatchet, however perfect, would have
imperfections. Even if it were absolutely perfect, the process of lining the device up
would be one of trial and error. So this device was unsatisfactory to the Greeks. It's
tempting to try to use a straightedge and compass to lay out the hatchet right on the
desired angle, but it also can't be done without trial and error.
It is possible to trisect the angle using a marked straightedge, but that's
not allowed by the ancient Greek rules, since a mark can't be lined up against another
point, line or arc without trial and error, and without some inherent error of alignment.
Likewise, you can solve the problem with two carpenters' squares, but that's also not
allowed since it also involves trial and error and since no carpenters' square will have
an absolutely perfect right angle.
There are subterfuges people have developed for seeming to get around these
restrictions. You can hold the compass against the ruler to measure distance;
technically you haven't "marked" the ruler but the effect is the same. There are
a variety of constructions that involve sliding the pivot point of the compass
along a line or arc; these all involve some measure of trial and error as well
(though the people who devise these constructions sometimes hotly deny it).
Using the compass for anything but drawing an arc around a fixed center is
forbidden.
I have modified this page several times as people come up with evasions of
the classical restrictions. So let's clarify the general principle: all
loopholes violate the rules.
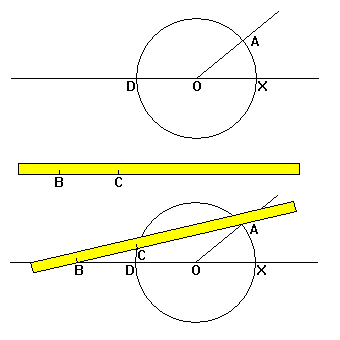 |
This is perhaps the simplest trisection using a marked straightedge. It
was discovered by Archimedes. Given the angle AOX, draw a circle of arbitrary radius
centered at O. Extend one side of the angle through the opposite side of the circle at D
(top). Mark off interval BC on the straightedge. BC = OX = radius of the circle.
Slide the straightedge so that B lies on line DOX, C lies on the circle and the
straightedge passes through A. Angle CBD is one-third of AOX. Note the element of trial
and error inherent in positioning the straightedge. |
Proof:
- Since BC=OC, angles CBD and COD are equal and angle BCO = 180-2CBD.
- And since OC = AO, angles OCA and OAC are equal.
- OCA + COD = 180 so OCA = 2CBD.
- The angles in triangle ABO sum to 180, so we have CBD + DOA + OAC = 180 = CBD + DOA +
2CBD.
- Rearranging, we get DOA = 180 - 3CBD, and since DOA + AOX = 180, AOX = 3CBD.
You can eliminate the marking by setting a compass with radius BC and sliding
the pivot along the line until B, C, and A are on a straight line. However, if
you do, there are two additional points to consider: where the radius of the
compass hits the circle (call it C') and where the radius hits the ruler (call
it C"). You can never be certain that C' = C" = C, regardless of how well the
points seem to agree. Even if the same pencil line covers all three
points, if they are different in the most microscopic degree, the construction
is not exact.
It also doesn't do to indulge in arm waving and say "slide the compass and
ruler until B, C, and A are on a straight line." We know point C exists
somewhere. You have to prove that you have actually found it. You have to be
able to prove that C' = C" = C.
| There are other curves besides circles that can be drawn, and can be used
to trisect the angle. The simplest, shown at right, is the Archimedean Spiral.
The radius of the spiral is proportional to azimuth. Obviously an angle can be trisected
by drawing an Archimedean Spiral over the angle, finding the radius where the other side
of the angle intersects the spiral, then trisecting the radius. Draw arcs from the
trisection points of the radius to the spiral, then draw radii through those points on the
spiral. In fact, an angle can be divided into any number of equal parts using
this method. |
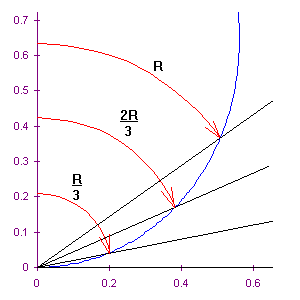 |
The problem with the Archimedean Spiral, or any other curve used to trisect the angle,
is that although you can construct an infinite number of points on the curve using a
straightedge and compass, you can't construct every point. However closely spaced
the points are, there will always be tiny gaps between them, so that any curve we draw
will always be approximate, not exact.
If you think about it, this whole business is actually pretty artificial. The Greek
compass, unlike modern ones, had a spring so that it snapped shut once it was lifted off
the page. Anyone who has ever had a compass change radius while drawing a circle can
picture the potential for error in such a device. Of course, we can do all the
constructions the Greeks did, in many cases a lot more simply, by using a compass that
stays fixed. To use something as error-prone as a spring-loaded compass, then worry about
possible imperfections in constructing a tool like the hatchet, or positioning a marked
straightedge, is completely arbitrary.
Also, if you think about it, the business of lining a straightedge up through two
points to draw a line also has a lot of trial and error about it - as much as the hatchet
tool. You line the straightedge up against one point, then position it against the other,
then go back and correct any shifting at the first point, and so on. Then, actually to
draw the line, you need to take into account the fact that any marking tool has finite
width, so that as often as not the drawn line doesn't pass exactly through the two points.
Renaissance instrument makers soon discovered this problem. They found out that
markings plotted using only compasses were more accurate than those made using
straightedges. They began devising alternative constructions that eliminated use of the
straightedge. Although the constructions were often more complex, they were still more
accurate than those that required straightedges. Mathematicians finally showed that every
construction that can be done with a compass and straightedge can be done with a compass
alone. The only qualification is that we define constructing two points on a given line as
equivalent to constructing the line itself.
Proving It Can't Be Done
Follow the Rules
Many people who "solve" the angle trisection problem inadvertently violate
the rules:
- You can only use a compass and a plain straightedge.
- You cannot use the straightedge for measuring, or put marks on it.
- You can only use the compass for drawing arcs around a fixed center. You
cannot slide the pivot.
- You cannot use a straightedge and compass to construct some other tool.
- You cannot use a straightedge and compass to construct some other curve.
- All loopholes and evasions of these restrictions violate the rules.
Why It's Impossible
The triple angle formula in trigonometry for the sine is: sin 3a = 3 sin a - 4
sin3a.
We can rewrite this to 4 sin3a - 3 sin a + sin 3a = 0
In other words, trisecting an angle amounts to solving a cubic equation. That's why
nothing has been said about doubling the cube. Doubling the cube amounts to finding the
cube root of two, that is, also solving a cubic equation. So algebraically, the two
constructions are equivalent. Squaring the circle is a bit more complicated.
Recall how the Pythagoreans, to their horror, found out that there are other kinds of
numbers than integers (whole numbers) and rational fractions. The process of discovering
all the types of numbers that exist turns out to be directly related to the proof that the
three classic problems are unsolvable. Since the time of Pythagoras, mathematicians have
discovered that there are many types of numbers:
- Integers (whole numbers), like 1,2 and 3
- Rational Numbers, numbers that are fractions involving integers, like 2/3, 1/2, and
19/10. Integers are also rational numbers, since they can be written as fractions like
1/1, 2/1, 3/1, and so on.
- Irrational Numbers, those that cannot be written as fractions involving integers. Almost
all roots, trigonometric functions and logarithms are irrational. So is pi.
- Positive and Negative Numbers. Also zero, which was unknown to the ancient Greeks.
- Imaginary Numbers, square roots of negative numbers. All other numbers are called Real
Numbers
- Complex Numbers, combinations of Imaginary and Real Numbers.
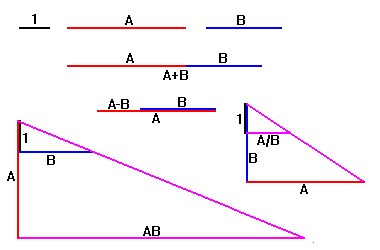 |
The final solution to the three famous problems of antiquity came from
studying classes and properties of numbers. Geometrical constructions can be considered
the equivalent of mathematical operations. For example, using only a straightedge, you can
add, subtract, multiply and divide: |
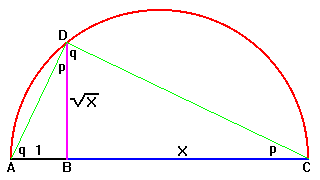 |
If you can draw circles, you can also construct square roots. Proof:
Triangle ACD is a right triangle since all angles inscribed in a semicircle are right
angles. So if one angle is p, q = 90 - p and the remaining angles have the values shown.
So triangles ABD and DBC are similar. Thus we can write BD/1 = X/BD, or BD squared = X.
Hence BD equals the square root of X. |
One of the first fruits of these studies was the discovery by the young Karl Friedrich
Gauss that it was possible, using a ruler and straightedge, to construct a polygon of 17
sides. This was something completely unsuspected. He also found that polygons of 257 and
65537 sides could be constructed. (Strictly speaking, Gauss only discovered it
was possible; other mathematicians devised constructions and showed that no
other polygons were possible, but Gauss made the pivotal discovery.) A number of books give constructions for the 17-sided
polygon; constructions for the other two have been devised but are hardly worth the
effort.
Numbers that can be expressed as combinations of rational numbers and square roots,
however complicated the combination, are called surds. Only surds can be
constructed using a compass and straightedge. We can now pose (and answer without
proof) the following questions:
- Are all numbers surds? (No - there are other kinds of numbers, just as the Pythagoreans
found there were other kinds of numbers than integers and rational fractions.)
- Are cube roots surds? (No - hence we cannot trisect the angle or duplicate the cube
using straightedge and compass. In fact higher roots like fifth roots, and so on, are also
not surds. Of course we ignore special cases like the cube root of 27 or the fifth root of
32, and so on.)
- Is pi a surd? (No - in fact pi belongs to yet another class of numbers called transcendental
numbers that cannot be obtained as the solution of any finite-sized polynomial.
Obviously, if pi is not a surd, then we can't square the circle, either.)
Gauss did more than just find new polygons. Building on his results, other
mathematicians showed that polygons of 2, 3, 5,
17, 257 ... sides are the only ones with prime numbers of sides that can be
constructed. (Of course you can also construct polygons by repeatedly bisecting the angles
of these polygons to construct polygons with 4, 6, 8, 10, 12, 16, etc. sides.
You can also construct polygons of 15 sides by combining the constructions for 3
and 5 sides, etc.) By
enumerating what was possible, he ruled out many other things as impossible.
In particular, 7 and 9-sided polygons cannot be constructed using straightedge and
compass. Constructing a 9-sided polygon requires trisecting a 120-degree angle. Since this
can't be done, obviously trisecting any desired angle is impossible.
Note, by the way, that 2=1+1, 3=21+1, 5=22+1, 17=24+1,
257=28+1, 65537=216+1. The numbers are all primes, and equal to some power of 2
plus one, and the exponents are all powers of 2. 65537 is the largest
prime of this type known, although extensive searches for larger ones have been
made.
"But You Have to Solve the Problem Geometrically"
Most people who still send solutions to the three classic problems to mathematics
departments don't have a clue how the problems were finally solved. Many seriously think
mathematicians just gave up and decreed the problems unsolvable.
The problems actually can't be solved because they require properties that a
straightedge and compass simply do not have. You can't draw an ellipse with a straightedge
and compass (although you can construct as many points on the ellipse as you like), so why
is it a shock that you can't trisect the angle, duplicate the cube, or square the circle?
You can't tighten nuts with a saw or cut a board with a wrench, and expecting a
straightedge and compass to do something beyond their capabilities is equally futile.
Here's another analogy: if you spend your entire life driving a truck, you might
eventually be lulled into thinking you can see the entire country from the highway. It's
only if you get out and walk or fly over the landscape that you discover there are a lot
of other places as well. Geometry with straightedge and compass creates a similar
illusion; eventually we believe the points we can construct are all the points that exist.
It was only when mathematicians began studying the properties of numbers that they found
out it wasn't so. Just as you have to get off the highway to see that other
places exist, to find the limitations of geometry you have to get outside of
geometry.
More mathematically literate angle trisectors are sometimes aware of the number-theory
approach, but reject it because they think a geometrical problem can only be properly
solved geometrically. But if the problem is that the solution requires capabilities beyond
those of a straightedge and compass, how in the world can that be discovered from within
geometry? Anyway, who says geometrical problems can only be properly solved geometrically?
The only thing that would justify that rule is some demonstration that the geometrical
solution to a problem and the algebraic solution yielded different results - and then
you'd have to prove the geometrical approach was the correct one. But there are no cases
where this has ever happened, so there is no justification for rejecting the algebraic
solution to the three classic problems. Indeed, it has been shown that if
there is an inconsistency anywhere in mathematics, it is possible to
prove any proposition whatsoever.
In fact, one of the most famous mathematical proofs of all times, Kurt
Godel's Incompleteness Theorem, showed that there is always an
"outside" to mathematics. Once a rule system gets complex enough (and
Euclidean geometry is plenty complex enough) it is always possible to make true statements that cannot be proven using
only the rules of that system. Thus is possible to make true
geometrical statements (like "angles cannot be trisected using ruler and
compass") that cannot be proven using the rules of geometry alone.
One Final Note
You can construct a 20-sided polygon with central angles of 18 degrees. You
can construct a 24-sided polygon with central angles of 15 degrees. Obviously
you can superimpose the constructions, and the difference between the two angles
is three degrees. That's the smallest integer value we can get using
straightedge and compass constructions. Since an arbitrary angle can't be
trisected, and we can't find any integer angles except multiples of three
degrees,
Therefore you cannot construct an exact one-degree angle with ruler and
compass!
I had one correspondent who got rather worked up over this. But what's so
special about 360 degrees? It's divisible by a lot of numbers, but so is 240. If
we defined a circle as having 240 degrees, each degree would be 1-1/2 of our
degrees. And we can construct 1-1/2 degrees exactly.
But so what?
We can't construct a one-degree angle exactly using a ruler and compass, but
we can subdivide line segments into any number of intervals. In
principle, we could construct a right triangle with one edge 100 million kilometers in length and another edge
1,745,506.492821758576 kilometers long at
right angles to it. The hypotenuse and the long edge define an angle of one
degree to an accuracy of 10-8 cm, the diameter of an atom.
You'll need a very big sheet of paper, a lot of patience, and a very
sharp pencil, but in Greek terms it's "possible". So we can construct
a one-degree angle to precision so fine it surpasses any possible practical
need.
Reference
Lots of books cover the mathematics behind the impossibility proofs. A really
good recent one is Robin Hartshorne, Geometry: Euclid and
Beyond, Springer, 2000. Warning: this is not fireside reading. The book is
very clear but it will take serious study to master it.
Return to Pseudoscience Index
Return to Professor Dutch's Home Page
Created 10 December 1999, Last Update
31 March 2006
Not an official UW Green Bay site



