MINIMUM SPANNING TREES STUDY GUIDE

Definition of edge-weighted graph and MST.

• What is a spanning tree?
• What is a minimum spanning tree?
• How many edges are in a (minimum) spanning tree of a graph with V vertices?
• Why do we make the simplifying assumptions that the graph is connected and the edge weights are distinct?

Cuts.

• What is a cut?
• How many cuts are there for a graph with V vertices?
• Cut property: given a cut, the crossing edge of minimum weight belongs to the MST. This is the most important point of this lecture, and you should be very familiar with its proof.

Manually performing Kruskal's and Prim's algorithms. These are easy and you should be able to do them even under the influence of powerful sedatives.

Why Kruskal's and Prim's algorithms work.

• Kruskal's algorithm is a special case of the generic greedy algorithm.
• Prim's algorithm is a special case of the generic greedy algorithm.

Implementing Kruskal's and Prim's algorithms.

• What sort of data do we track in Kruskal's algorithm, and which data structures do we use to track this data?
• What is the running time for typical implementations of these data structures?
• What sort of data do we track in Lazy Prim's algorithm, and what data structures do we use to track this data?
• What is the running time for typical implementations of these data structures?
• For Eager Prim's, why do we track vertices instead of edges? What does this do to our space requirements?
• What is the special data structure that we use to track vertices and their best known distance?
• How do we change the priority of a vertex using this special data structure (you should be able to give an example of a method call)?

Recommended Problems

C level

1. Consider the following weighted graph.
   
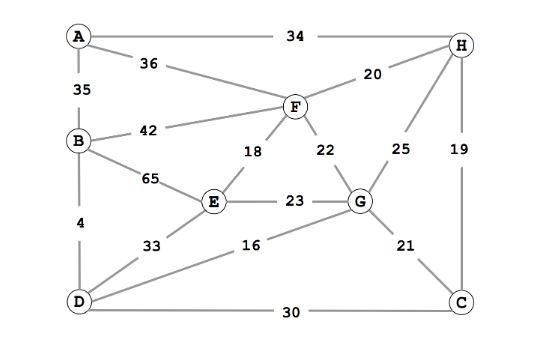
   Give the list of edges in the MST in the order that Kruskal's algorithm includes them.
   Give the list of edges in the MST in the order that Prim's algorithm includes them. Start Prim's algorithm from vertex A. Answers
   Kruskal: B-D D-G E-F C-H F-H C-G A-H
   Prim: A-H C-H F-H E-F C-G D-G B-D
2. Consider the following undirected weighted graph.
   
   Give the list of edges in the MST in the order that Kruskal's algorithm includes them.
   Give the list of edges in the MST in the order that Prim's algorithm includes them. Start Prim's algorithm from vertex F. Answers
   Kruskal: 4,9,18,19,21,22,23,30
   Prim: 18,23,21,19,30,4,9,22
3. Consider the following undirected weighted graph.
   
   Give the list of edges in the MST in the order that Kruskal's algorithm includes them.
   Give the list of edges in the MST in the order that Prim's algorithm includes them. Start Prim's algorithm from vertex A. Answers
   Kruskal: 1 2 3 5 6 7 8 12
   Prim: 6 1 3 2 5 7 8 12
4. Spring 12 Final, #4a, #4b
5. Would Kruskal's or Prim's algorithm work with edge-weighted digraphs?

B level

1. Using the weighted undirected graph from C level #3, suppose that the edge D - I of weight w is added to the graph. For which values of w is the edge D - I in a MST? Answers
   w = 8
2. Fall 12 Final, #4a, #4b, #4c, #4d
3. Textbook 4.3.8 - this is a particularly handy concept!
4. Textbook 4.3.12
5. Textbook 4.3.13
6. Textbook 4.3.20
7. True or False: Given any two components that are generated as Kruskal's algorithm is running (but before it has completed), the smallest edge connecting those two components is part of the MST.
8. Textbook 4.3.19 - to be clear, for each vertex v, we maintain edgeTo[v] and distTo[v] and to find the nontree vertex with the smallest distTo[], we scan through the entire distTo[] array.

A level

1. You are given an edge-weighted undirected graph, using the adjacency list representation, together with the list of edges in its minimum spanning tree (MST). Describe an efficient algorithm for updating the MST, when each of the following operations is performed on the graph. Assume that common graph operations (e.g., DFS, BFS, finding a cycle, etc.) are available to you, and don't describe how to re-implement them.
   1. Update the MST when the weight of an edge that was not part of the MST is decreased. Give the order-of-growth running time of your algorithm as a function of V and/or E.
   2. Update the MST when the weight of an edge that was part of the MST is decreased. Give the order-of-growth running time of your algorithm as a function of V and/or E.
   3. Update the MST when the weight of an edge that was not part of the MST is increased. Give the order-of-growth running time of your algorithm as a function of V and/or E.
   4. Update the MST when the weight of an edge that was part of the MST is increased. Give the order-of-growth running time of your algorithm as a function of V and/or E.
   Answers
   1. Add the updated edge to the MST, which will create a cycle. Run a cycle detector on the augmented MST, to find the edges in that cycle. Loop over those edges, keeping track of the one having maximum weight. Remove that maximum-weight edge, restoring an MST. Finding a cycle (using something like DFS) is normally O(E), but the augmented MST has only V edges, hence runs in O(V) time. Similarly, finding the max-weight edge in that cycle can be done in O(V) time. So, the running time is O(V). (6 points)
   2. Do nothing, since this can't affect the MST. Constant time. (2 points)
   3. Do nothing, since this can't affect the MST. Constant time. (2 points)
   4. Remove the edge in question from the MST, which will disconnect it into two connected components. Run DFS from one of the endpoints of that edge, marking all vertices in one of those components. (The unmarked vertices form the other connected component.) Now loop over all edges, keeping track of the minimum-weight edge having one endpoint in the marked set and its other endpoint in the unmarked set. Add that minimum-weight edge, restoring an MST. DFS to find a connected component will run in O(E) time, as will finding the minimum-weight edge spanning the two connected components. So, the running time is O(E). (6 points)
2. Given a minimum spanning tree T of a weighted graph G , describe an O ( V ) algorithm for determining whether or not T remains a MST after an edge x - y of weight w is added Answers
   Find the unique path between x and y in T . This takes O ( V ) time using DFS because there are only V - 1 edges in T . We claim the edge T remains an MST if and only if w is greater than or equal to the weight of every edge on the path.

   If any edge on the path has weight greater than w , we can decrease the weight of T by swapping the largest weight edge on the path with x - y . Thus, T does not remain an MST.

   If w is greater than or equal to the weight of every edge on the path, then the cycle property asserts that x - y is not in some MST (because it is the largest weight edge on the cycle consisting of the path from x to y plus the edge x - y ). Thus, T remains an MST.

3. Textbook 4.3.26

Just for fun

1. Figure out if Kruskal's, Prim's Lazy, or Prim's Eager algorithm are faster on "typical" graphs. Use the code from the booksite.