BINARY SEARCH TREES
BST basics.
Know the definition of a BST and how to search and insert.
Recursive BST code.
You should be able to read recursive BST code.
You will write recursive BST code on the k-d tree programming assignment.
In-order traversal.
Understand how to perform an inorder traversal.
Treesort.
Understand how to use a BST to sort items. Insert all the items, then perform an inorder traversal.
This algorithm is similar to quicksort, where each node corresponding to a partitioning item
that subdivides its descendants into smaller keys and larger keys.
Symbol table performance.
Understand the performance of a BST based symbol table in the
best, worst, and average (shuffled) case, with an emphasis on the fact that
the height of a tree is the key factor.
Recommended Problems
C level
- What is the best case BST height? Worst case?
- If shuffling guarantees log n tree height (probabilistically),
why don't we simply shuffle our input data before building our BST based symbol table to avoid worst case behavior?
- Textbook 3.2.3, but give only two orderings.
- Textbook 3.2.4
-
From the trees shown in figure A below, circle the correct binary tree (not necessarily a BST) that would produce both of the following traversals:
In-order: AQVNBRMSP
Pre-order: BQAVNRSMP
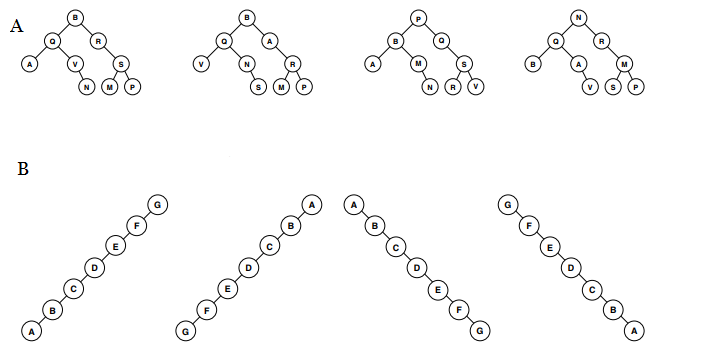
From the trees shown in figure B below, circle the correct Binary Search Tree that would produce the following traversal:
Post-order: ABCDEFG
Answers
In figure A, the first or leftmost tree. In figure B, the first or leftmost tree.
B level
- Stable 2-way partitioning is a partitioning procedure in which items that are smaller
than the pivot are kept in the same relative order after partitioning, and likewise with larger items.
For example, if we stably partition GADFLY on G, we'd get ADFGLY. Perform an entire
quicksort using stable partitioning on the array [5, 3, 2, 1, 9, 7, 6],
and record the compares you make along the way. Build the BST for this array.
Observe that the same exact compares were made.
What are the advantages and disadvantages of this stable 2-way partitioning algorithm
compared to the version we discussed in the Quicksort lecture?
- Textbook 3.2.22 (pretty easy, but good to do)
- Textbook 3.2.23
- Textbook 3.2.24 (so easy it might seem hard)
-
If you know that a tree is a BST, which of the following is or is not always sufficient to reconstruct it?
For each one, write yes if it is enough to reconstruct the tree, or no if it is not.
Pre-order traversal:
In-order traversal:
Post-order traversal:
Level-order traversal:
Answers
Yes, no, yes, yes. Or put another way, only in-order is not sufficient.
A level
- Write your own pre-order or post-order traversal code.

