The instructors plan to grade the final, May 20. They have scheduled 8
hours for it. Each instructor prefers to grade only a certain subset of the 11 problems. They
have represented their preferences in a graph in which a grader is connected to a problem if
they are willing to grade it.
Each grader has a grading speed, and each problem has a grading difficulty. If a problem with
difficulty d is graded by an instructor with speed s, it will take d/s minutes to grade. There
are N problems and M instructors; S students took the exam.
Design an algorithm to determine if the instructors will be
able to finish grading within the scheduled 8 hours, respecting their grading preferences.
What is the order-of-growth worst-case running time of your algorithm in terms of M and N?
Assume that the speeds and difficulties are bounded by a constant.
Hint: formulate it as a max-flow problem and invoke a known algorithm for solving max-flow.
You might want to draw a graph to illustrate how you construct a max-flow problem.
Answers
Create a graph with one vertex for each problem and one for each as shown. The source →
problem capacities represent the grading effort needed for each problem. The grader → sink
capacities represent the grading capability of each instructor in 8 hours. The problem →
grader edges are as in the input graph.
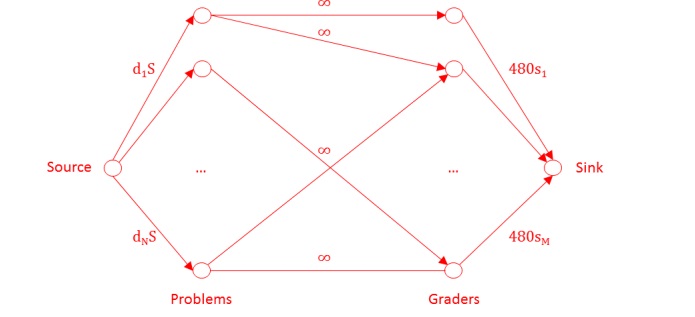
Check if the max flow equals ∑(i=1, N) d
iS using the Ford-Fulkerson algorithm. If it is, it means the grading effort needed for each problem can be partitioned among the instructors
without any instructor exceeding their 8-hour grading capability.
The running time is VE
2 with the shortest-augmenting-path heuristic. Here V = M + N + 2
and E ≤ MN + M + N, the running time is M
2N
2 (M + N).
 Check if the max flow equals ∑(i=1, N) diS using the Ford-Fulkerson algorithm. If it is, it means the grading effort needed for each problem can be partitioned among the instructors
without any instructor exceeding their 8-hour grading capability.
The running time is VE2 with the shortest-augmenting-path heuristic. Here V = M + N + 2
and E ≤ MN + M + N, the running time is M2N2 (M + N).
Check if the max flow equals ∑(i=1, N) diS using the Ford-Fulkerson algorithm. If it is, it means the grading effort needed for each problem can be partitioned among the instructors
without any instructor exceeding their 8-hour grading capability.
The running time is VE2 with the shortest-augmenting-path heuristic. Here V = M + N + 2
and E ≤ MN + M + N, the running time is M2N2 (M + N).