Data Compression Study Guide

DATA COMPRESSION STUDY GUIDE

Terminology and Basics

Why compress? To save space and time.
How does compression work? Compression takes advantage of structure within data.
What sort of data does not compress well? Random data.
Lossy compression can further reduce file sizes by throwing away unimportant information.
What is the compression ratio?
Why can no compression algorithm possibly compress all bit streams?
What fraction of bitstreams can be compressed in half by a general-purpose algorithm?

Run-length coding

Takes advantage of repeated binary digits.
How do you handle runs of length more than 2^M?

Huffman coding

Basic idea: Variable length codewords to represent fixed length characters. More common characters are represented by shorter codewords.
What is a prefix-free code? Why is it important that Huffman coding use a prefix-free code? Would encoding work with a non prefix-free code? Would decoding work?
Why is it necessary to transmit the coding trie? Why don't we have to do something similar with run length encoding or LZW?
Why do we typically use an array for encoding and a trie for decoding?
You do not need to know the specifics of the binary representaiton of the Huffman trie. However, you should conceptually understand the idea of transmitting/reading the trie using an preorder traversal.

LZW

Basic idea: Fixed length codewords to represent variable length strings. More common characters are represented by shorter codewords.
Why do we typically use a trie for encoding and an array for decoding?
How do you handle the 'strange' case (where a codeword is seemingly not in the table during decoding)?

Recommended Problems

C level

Decode each of the following LZW-encoded messages or explain briefly why it is not a valid LZW-encoded message. (Recall that codeword 80 is reserved to signify end of file.)

41 42 43 44 80 
42 41 4E 82 41 80
42 41 83 80
41 42 81 82 80
41 42 81 83 80
42 41 4E 44 41 4E 41 80

Answers

  LZW-encoded message     original message or brief explanation why invalid
  -------------------     -------------------------------------------------
  42 41 4E 82 41 80       B A N A N A
  42 41 83 80             not possible since 83 would not yet be in table
  41 42 81 82 80          A B A B B A
  41 42 81 83 80          A B A B A B A (see p. 843 of textbook)
  42 41 4E 44 41 4E 41 80 not possible because of second occurrence of 41 4E

Fall 2012 Final, #12 (Huffman)
Spring 2012 Final, #10 (BW)
Textbook 5.5.3

B level

Consider the following Huffman trie of a message over the 5-character alphabet {A, B, C, D, E}:

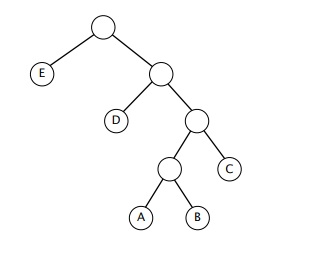
Identify each statement with the best matching description (below tagged with letters A to D).
---- The frequency of A is strictly less than the frequency of B.
---- The frequency of C is greater than or equal to the frequency of A.
---- The frequency of D is strictly greater than the frequency of A.
---- The frequency of D is greater than or equal to that of A, B, and C combined.
---- The frequency of E is strictly less than that of
```
    A, B, and C combined.
    A. True for all messages.
    B. False for all messages.
    C. Depends on the message.
```
Answers
C A A C B
i. The frequency of A can be less than the frequency of B or it can be equal to the frequency of B.
ii. Since A and B are merged first, they have are symbols that have the smallest frequencies.
iii. Clearly freq(D) >= freq(A). Suppose freq(D) = freq(A). Then, since freq(D) >= freq(C) >= freq(A), we must have freq(D) = freq(C) = freq(A). In this case, C and D would be merged (instead of C and {A, B}).
iv. If A, B, and C have frequency 1, then D could have frequency 2 or 3 and produce the same subtree.
v. If the frequency of E is strictly less than that of A, B, and C combined, then so is the frequency of D. Hence, D and E would be merged. Note that if a character appears 0 times, then it will not appear in the Huffman trie
Textbook 5.5.13
Textbook 5.5.17

A level

Fall 2012 Final, #13