TRIES STUDY GUIDE
Terminology and Basics
- Length of string keys = L.
- Alphabet size = R.
- You should be able to build either an R-way Trie and TST.
You should be able to search in either a R-way Trie and TST.
You should be able to delete from an R-way trie.
You should appreciate how a TST can become unbalanced with inserts.
- Given a graphical depiction of either an R-way trie or TST, you should be able
to tell which keys are in the trie.
Hash Tables and LLRBs with String keys
- With String keys, we don't want to think about counting compareTo()
or hashCode() and equals() calls. Why? What do we think about instead?
- Know (but you do not have to prove) that LLRBs take order of growth lg2 N charAt()
calls to compare random strings. Based on this, a hit is order L + lg2 N.
- Understand why hash tables are L charAt() calls on a hit or miss (assuming no collisions!)
Tries
- Special structure such that you only look at each letter one time. Trivially, misses
and hits have a maximum run time of L.
- Be aware that for random inputs, search misses only take an average of logR N.
- Why do R-way tries use such a huge amount of memory? How much memory in terms of L and R?
- What are the two ways of determining that a key does not exist in a trie?
TSTS
- When looking for a single character, why is it possible to follow as many as R
links before you complete the search for that character?
- If the TST is balanced, typical case inserts and hits cost L + lg N character compares,
and typical misses cost lg N character compares.
- If the TST is not balanced, worst case hits, misses, and inserts all include H,
where H is the height of the tree.
Recommended Problems
C level
- Fall 2012 Final, #8
-
Consider the following ternary search trie, with string keys and integer values.
List the strings that are keys in the TST.
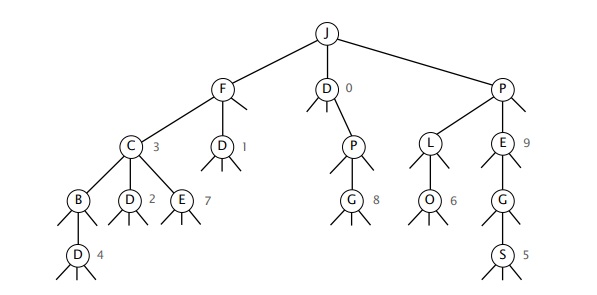
Answers
BD C CD E FD JPG PEGS
- Textbook 5.2.3, 5.2.4
B level
- Spring 2012 Final, #9
- Textbook 5.2.21 (just design the API)
- When would we want to use an R-way trie instead of a TST?
- Give a worst case input that causes a TST to be unbalanced (and thus slow).
- Is the number of character compares in an R-way trie strictly better than for
an LLRB? For a hash table? Is a trie guaranteed to be faster
in overall run time than an LLRB or a hash table?
A level
- When might we want to use a hash table instead of a TST?
- What would happen if we had an R-way trie where we keep our next nodes in a linked list?
How would this affect memory performance? Timing? What if we used an LLRB? A hash table?

