SHORTEST PATHS STUDY GUIDE

Graph Representation

• Use DirectedEdge instead of Edge.
• Adjacency list tracks only edges pointing from vertex.

Shortest path representation

• Can represent shortest path as a tree.
• In Java, we represent the shortest path tree with two arrays: distTo[] and edgeTo[].

Edge relaxation

• What does it mean to relax an edge? Update shortest path tree (edgeTo[] and distTo[]) to reflect the information contained in that edge. What does it mean to relax a vertex?
• The code for relax should be second nature.
• What are the shortest paths optimality conditions? Why is it true?
• What is the generic shortest path algorithm? Why does it always eventually get the right answer?

Manually performing Dijkstra's algorithm, Acyclic Shortest Paths algorithm, and Bellman-Ford algorithm. These should be very easy to manully execute.

Dijkstra's algorithm

• Edge weights must be nonnegative.
• Relax the vertices in increasing order of distance from s.
• Important invariant: Once a vertex belongs to the shortest path tree, its distTo[] and edgeTo[] entries never change. Why is this invariant true? How does it prove correctness?
• Why is the running time (V + E) log V if we use a binary heap to implement the priority queue? Why do the book and slides just say E log V? If we change our priority queue implementation, how does the running time change
• How is Dijkstra's algorithm similar to Prim's algorithm? How is it dffferent?

Acyclic shortest paths

• Digraph must be a DAG (but edge weights can be positive or negative).
• Relax the vertices in topologial order.
• Why does it work?
• Why is the running time E + V?

Bellman-Ford algorithm

• Edge-weighted digraph must have no negative cycles.
• Relax all the edges. Then relax them all again. And again. Repeat this V times. You are done.
• Running time is obviously E V.
• Proof: After ith relaxation of all E edges, the algorithm has found a path that is at least as short as the shortest path from s to v containing <= i edges. There are at most V-1 edges between any two vertices in the shortest path tree (otherwise it is not a tree).

Recommended Problems

C level

1. Simulate Dijkstra's algorithm on the edge-weighted digraph below, starting from vertex 0.
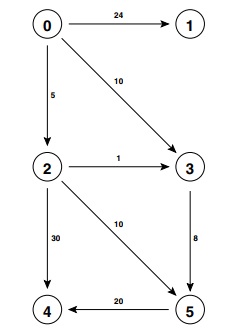
   1. Give all the distTo[] and edgeTo[] values that result.
   2. What is the maximum number of items in the priority queue?
   3. What is the last vertex popped from the priority queue?
   4. What letter is spelled out by the edges of the shortest-path tree (SPT) computed by Dijksta's algorithm?
   Answers
   (a)

   	distTo[ ]	edgeTo[ ]
   0	0	-
   1	24	0
   2	5	0
   3	6	2
   4	34	5
   5	14	3

   
   (b) 4, (c) 4, (d) S
2. Textbook 4.3.1 and 4.4.1

B level

1. Spring 2012 Final, #5
2. Fall 2012 Final, #5
3. Suppose that you are running Dijkstra's algorithm on the edge-weighted digraph (table below), starting from a source vertex s. The table (second table below) gives the edgeTo[] and distTo[] values immediately after vertex 2 has been deleted from the priority queue and relaxed.

   edge	weight	edge	weight
   0 --> 2	6.0	5 --> 1	12.0
   0 --> 4	6.0	5 --> 2	1.0
   0 --> 5	17.0	5 --> 4	3.0
   1 --> 3	17.0	5 --> 7	10.0
   2 --> 5	11.0	5 --> 8	4.0
   2 --> 7	6.0	6 --> 0	12.0
   3 --> 0	1.0	6 --> 1	5.0
   3 --> 10	3.0	6 --> 2	1.0
   3 --> 1	25.0	6 --> 4	9.0
   3 --> 6	13.0	6 --> 9	4.0
   3 --> 8	9.0	7 --> 1	7.0
   4 --> 5	3.0	7 --> 5	11.0
   4 --> 6	4.0	7 --> 9	6.0
   4 --> 7	3.0	10 --> 1	15.0
   4 --> 8	1.0	10 --> 5	2.0
   4 --> 9	15.0	10 --> 8	7.0

     Dijkstra in progress
     v distTo[] edgeTo[]
     0  1.0     3 --> 0
     1 17.0     5 --> 1
     2  6.0     5 --> 2
     3  0.0     null
     4  7.0     0 --> 4
     5  5.0    10 --> 5
     6 13.0     3 --> 6
     7 12.0     2 --> 7
     8  9.0     3 --> 8
     9  8       null
     10 3.0     3 --> 10
   

   1. Give the order in which the first 5 vertices were deleted from the priority queue and relaxed.
   2. Modify the table (just above, titled "Dijkstra in progress") to show the values of the edgeTo[] and distTo[] arrays immediately after the next vertex has been deleted from the priority queue and relaxed. Circle those values that changed.
   Answers
   1. 3 0 10 5 2
      It is not necessary to run the algorithm from the beginning to deduce this because Dijkstra's algorithm considers the vertices in increasing order of distance from the source.
   2. The next vertex to relax is 4.

     v distTo[] edgeTo[]
     0  1.0 3 --> 0
     1 17.0 5 --> 1
     2  6.0  5 --> 2
     3  0.0  null
     4  7.0  0 --> 4
     5  5.0 10 --> 5
     6 11.0 4 --> 6
     7 10.0 4 --> 7
     8  8.0 4 --> 8
     9 22.0 4 --> 9
     10 3.0 3 --> 10
   

4. Think about how to solve the undirected version of the shortest paths problem. Why is it easy for graphs with positive edge weights? Why is it hard if we include negative edge weights?
5. Textbook 4.4.25
6. Since Prim's algorithm and Dijkstra's algorithm are so similar, why do we need to check for cycles in Prim's, but not in Dijkstra's?
7. Textbook 4.4.42 and 4.4.44

A level

1. Textbook 4.4.34
2. Textbook 4.4.37