

Seam-carving is a content-aware image resizing technique where the image is reduced in size by one
pixel of height (or width) at a time.
A vertical seam in an image is a path of pixels connected from the top to the bottom
with one pixel in each row;
a horizontal seam is a path of pixels connected from the left to the right
with one pixel in each column.
Below left is the original 505-by-287 pixel image; below right is the result after removing
150 vertical seams, resulting in a 30% narrower image.
Unlike standard content-agnostic resizing techniques (such as cropping and scaling),
seam carving preserves the most interest features (aspect ratio, set of objects present,
etc.) of the image.
Although the underlying algorithm is simple and elegant, it was not discovered until 2007 by Shai Avidan and Ariel Shamir. It is now a core feature in Adobe Photoshop (thanks to a Princeton graduate student) and other computer graphics applications.


In this assignment, you will create a data type that resizes a W-by-H image using the seam-carving technique. Finding and removing a seam involves three parts and a tiny bit of notation:
| (0, 0) | (1, 0) | (2, 0) |
| (0, 1) | (1, 1) | (2, 1) |
| (0, 2) | (1, 2) | (2, 2) |
| (0, 3) | (1, 3) | (2, 3) |
Warning: this is the opposite of the standard mathematical notation used in linear algebra, where (i, j) refers to row i and column j and (0, 0) is at the lower-left corner.
We also assume that the color of each pixel is represented in RGB space, using three integers between 0 and 255. This is consistent with the java.awt.Color data type.
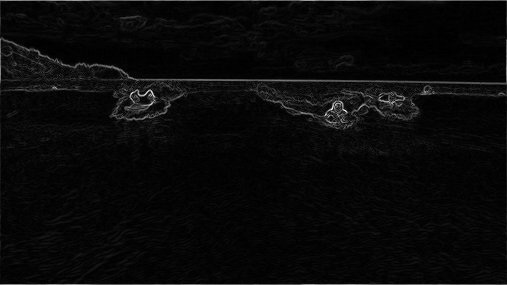
The energy is high (white) for pixels in the image where there is a rapid color gradient (such as the boundary between the sea and sky and the boundary between the surfing Josh Hug on the left and the ocean behind him). The seam-carving technique avoids removing such high-energy pixels.
Seams cannot wrap around the image (e.g., a vertical seam cannot cross from the leftmost column of the image to the rightmost column).
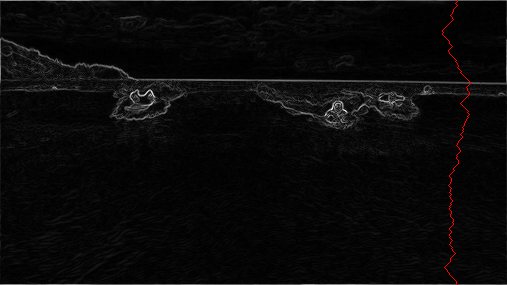
The SeamCarver API. Your task is to implement the following mutable data type:
public class SeamCarver {
public SeamCarver(Picture picture) // create a seam carver object based on the given picture
public Picture picture() // current picture
public int width() // width of current picture
public int height() // height of current picture
public double energy(int x, int y) // energy of pixel at column x and row y
public int[] findHorizontalSeam() // sequence of indices for horizontal seam
public int[] findVerticalSeam() // sequence of indices for vertical seam
public void removeHorizontalSeam(int[] seam) // remove horizontal seam from current picture
public void removeVerticalSeam(int[] seam) // remove vertical seam from current picture
public static void main(String[] args) // do unit testing of this class
}
Corner cases. Your code should throw an exception when a constructor or method is called with an invalid argument, as documented below:
As an example, consider the 3-by-4 image (supplied as 3x4.png) with RGB values—each component is an integer between 0 and 255—as shown in the table below:

Rx(1, 2) = 255 − 255 = 0,yielding Δx2(1, 2) = 22 + 2042 = 41620;
Gx(1, 2) = 205 − 203 = 2,
Bx(1, 2) = 255 − 51 = 204,
and pixels (1, 1) and (1, 3) for the y-gradient
Ry(1, 2) = 255 − 255 = 0,yielding Δy2(1, 2) = 1022 = 10404.
Gy(1, 2) = 255 − 153 = 102,
By(1, 2) = 153 − 153 = 0,
Thus, the energy of pixel (1, 2) is \(\sqrt{41620 + 10404} = \sqrt{52024}\). Similarly, the energy of pixel (1, 1) is \(\sqrt{204^2 + 103^2}= \sqrt{52225}\).
Rx(1, 0) = 255 − 255 = 0,yielding Δx2(1, 0) = 2042 = 41616;
Gx(1, 0) = 101 − 101 = 0,
Bx(1, 0) = 255 − 51 = 204,
and pixels (1, 3) and (1, 1) for the y-gradient
Ry(1, 0) = 255 − 255 = 0,yielding Δy2(1, 2) = 1022 = 10404.
Gy(1, 0) = 255 − 153 = 102,
By(1, 0) = 153 − 153 = 0,
Thus, the energy of pixel (1, 2) is \(\sqrt{41616 + 10404} = \sqrt{52020}\).
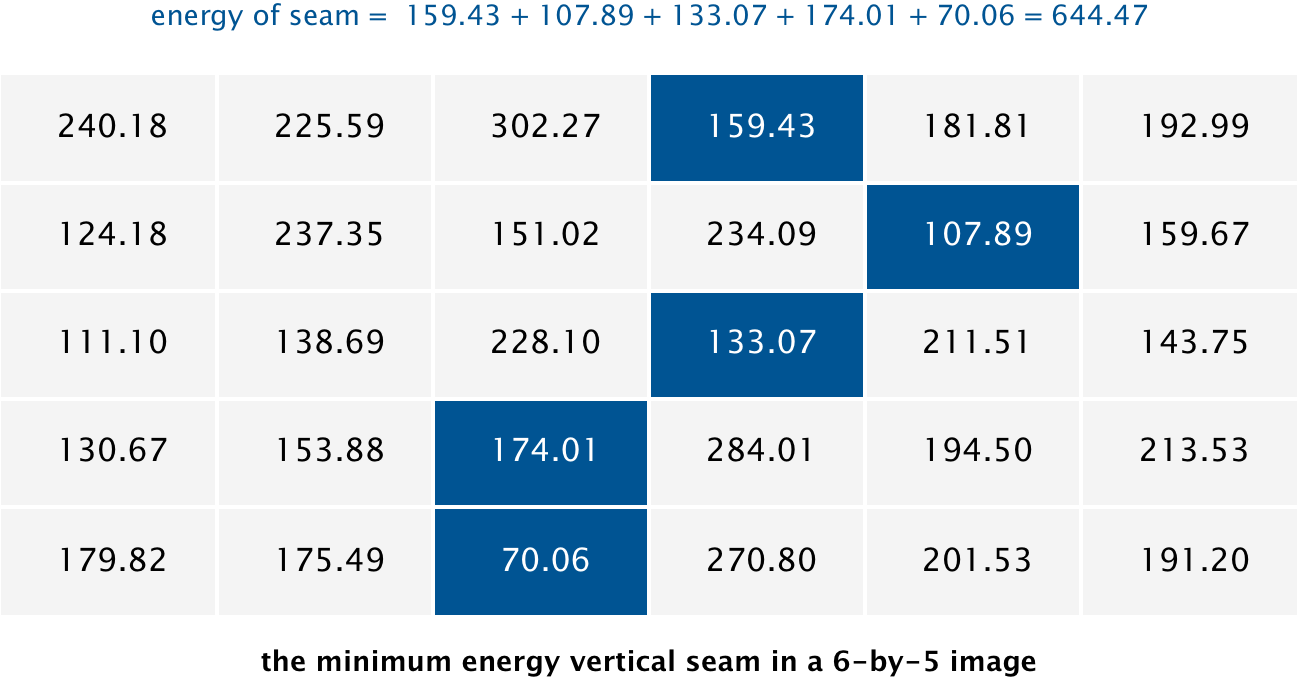
The minimum energy vertical seam is highlighted in blue. In this case, the method findVerticalSeam() should return the array { 3, 4, 3, 2, 2 } because the pixels in the minimum energy vertical seam are (3, 0), (4, 1), (3, 2), (2, 3), and (2, 4). Remember that seams cannot wrap around the image. When there are multiple vertical seams with minimal total energy, your method can return any such seam.
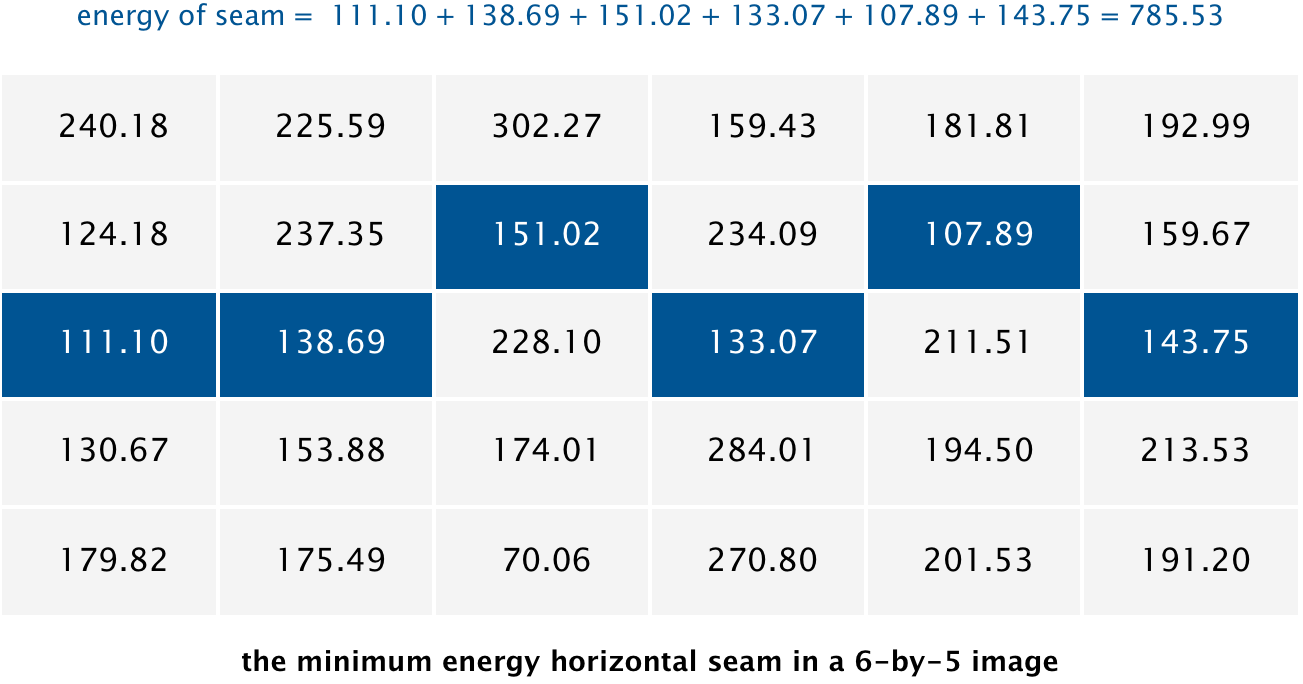
Finding a horizontal seam. The behavior of findHorizontalSeam() is analogous to that of findVerticalSeam() except that it returns an array of length W such that entry x is the row number of the pixel to be removed from column x of the image. For the 6-by-5 image, the method findHorizontalSeam() should return the array { 2, 2, 1, 2, 1, 2 } because the pixels in the minimum energy horizontal seam are (0, 2), (1, 2), (2, 1), (3, 2), (4, 1), and (5, 2).
Performance requirements. The width(), height(), and energy() methods should take constant time in the worst case. All other methods should run in time proportional to W H (or better) in the worst case.
Analysis of running time. Estimate empirically the running times (in seconds) to remove one row and one column from a W-by-H image as a function of W, and H. Use tilde notation to simplify your answer. Answer the relevant questions in the readme.txt file.
Submission. Submit SeamCarver.java, and any other files needed by your program (excluding those in algs4.jar). You may not call any library functions other than those in java.lang, java.util, java.awt.Color, and algs4.jar. Finally, submit a readme.txt file and answer the questions.
This assignment was developed by Josh Hug, Maia Ginsburg, and Kevin Wayne.