Remark: This computes the number of bits in the binary representation of N, which also equals 1 + floor(log2 N) when N is positive. This quantity arises in information theory and the analysis of algorithms.
% java Ordered 10 17 49 true % java Ordered 49 17 10 true % java Ordered 10 49 17 false
Write a program RGBtoCMYK.java that converts RGB to CMYK. Read three integers red, green, and blue from the command line, and print the equivalent CMYK values using these formulas:
Hint. Math.max(x, y) returns the maximum of x and y.
% java RGBtoCMYK 75 0 130 // indigo cyan = 0.423076923076923 magenta = 1.0 yellow = 0.0 black = 0.4901960784313726
If all three red, green, and blue values are 0, the resulting color is black, so you should output 0.0, 0.0, 0.0 and 1.0 for the cyan, magenta, yellow and black values, respectively.
% java Checkerboard 4 % java Checkerboard 5 * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
-
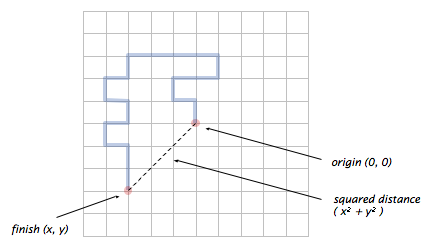
Write a program RandomWalker.java that takes an integer command-line
argument N and simulates the motion of a random walker for N
steps. After each step, print the location of the random walker, treating
the lamp post as the origin (0, 0).
Also, print the square of the final distance from the origin.
% java RandomWalker 10 % java RandomWalker 20 (0, -1) (0, 1) (0, 0) (-1, 1) (0, 1) (-1, 2) (0, 2) (0, 2) (-1, 2) (1, 2) (-2, 2) (1, 3) (-2, 1) (0, 3) (-1, 1) (-1, 3) (-2, 1) (-2, 3) (-3, 1) (-3, 3) squared distance = 10 (-3, 2) (-4, 2) (-4, 1) (-3, 1) (-3, 0) (-4, 0) (-4, -1) (-3, -1) (-3, -2) (-3, -3) squared distance = 18 -
Write a program RandomWalkers.java that takes two integer
command-line arguments N and T.
In each of T independent experiments,
simulate a random walk of N steps and compute the squared distance.
Output the mean squared distance (the average of the T squared distances).
% java RandomWalkers 100 10000 % java RandomWalkers 400 2000 mean squared distance = 101.446 mean squared distance = 383.12 % java RandomWalkers 100 10000 % java RandomWalkers 800 5000 mean squared distance = 99.1674 mean squared distance = 811.8264 % java RandomWalkers 200 1000 % java RandomWalkers 1600 100000 mean squared distance = 195.75 mean squared distance = 1600.13064
As N increases, we expect the random walker to end up farther and farther away from the origin. But how much farther? Use RandomWalkers to formulate a hypothesis as to how the mean squared distance grows as a function of N. Use T = 100,000 trials to get a sufficiently accurate estimate.
Remark: this process is a discrete version of a natural phenomenon known as Brownian motion. It serves as a scientific model for an astonishing range of physical processes from the dispersion of ink flowing in water, to the formation of polymer chains in chemistry, to cascades of neurons firing in the brain.
Remark: the central limit theorem, a key result in probability and statistics, asserts that the shape of the resulting histogram tends to the ubiquitous bell curve (Gaussian distribution) if the number of dice and rolls is large.
