Programming Assignment 5: Kd-Trees

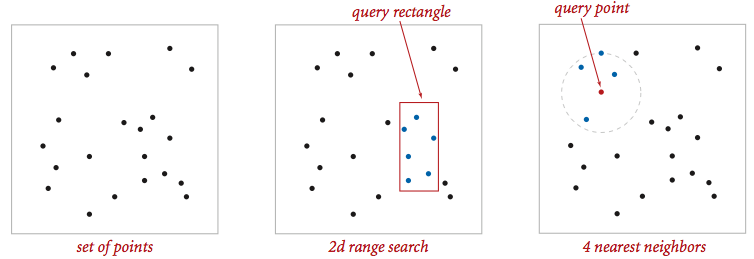
Geometric primitives. To get started, use the following geometric primitives for points and axis-aligned rectangles in the plane.

Use the immutable data type Point2D.java (part of algs4.jar) for points in the plane. Here is the subset of its API that you may use:

public class Point2D implements Comparable<Point2D> {
   public Point2D(double x, double y)              // construct the point (x, y)
   public  double x()                              // x-coordinate
   public  double y()                              // y-coordinate
   public  double distanceSquaredTo(Point2D that)  // square of Euclidean distance between two points
   public     int compareTo(Point2D that)          // for use in an ordered symbol table
   public boolean equals(Object that)              // does this point equal that?
   public    void draw()                           // draw to standard draw
   public  String toString()                       // string representation
}

public class RectHV {
   public    RectHV(double xmin, double ymin,      // construct the rectangle [xmin, xmax] x [ymin, ymax]
                    double xmax, double ymax)      // throw a java.lang.IllegalArgumentException if (xmin > xmax) or (ymin > ymax)
   public  double xmin()                           // minimum x-coordinate of rectangle
   public  double ymin()                           // minimum y-coordinate of rectangle
   public  double xmax()                           // maximum x-coordinate of rectangle
   public  double ymax()                           // maximum y-coordinate of rectangle
   public boolean contains(Point2D p)              // does this rectangle contain the point p (either inside or on boundary)?
   public boolean intersects(RectHV that)          // does this rectangle intersect that rectangle (at one or more points)?
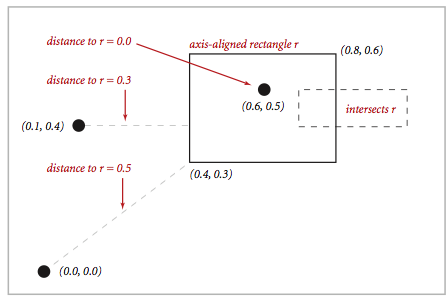
   public  double distanceSquaredTo(Point2D p)     // square of Euclidean distance from point p to closest point in rectangle
   public boolean equals(Object that)              // does this rectangle equal that?
   public    void draw()                           // draw to standard draw
   public  String toString()                       // string representation
}

Brute-force implementation. Write a mutable data type PointSET.java that represents a set of points in the unit square. Implement the following API by using a red-black BST (using either SET from algs4.jar or java.util.TreeSet, do not try to implement your own red-black BST).

public class PointSET {
   public    PointSET()                            // construct an empty set of points
   public           boolean isEmpty()              // is the set empty?
   public               int size()                 // number of points in the set
   public              void insert(Point2D p)      // add the point p to the set (if it is not already in the set)
   public           boolean contains(Point2D p)    // does the set contain the point p?
   public              void draw()                 // draw all of the points to standard draw
   public Iterable<Point2D> range(RectHV rect)     // all points in the set that are inside the rectangle
   public    Point2D nearest(Point2D p)            // a nearest neighbor in the set to p; null if set is empty
   public static void main(String[] args)          // unit testing of the methods
}

2d-tree implementation. Write a mutable data type KdTree.java that uses a 2d-tree to implement the same API (but replace PointSET with KdTree). A 2d-tree is a generalization of a BST to two-dimensional keys. The idea is to build a BST with points in the nodes, using the x- and y-coordinates of the points as keys in strictly alternating sequence, starting with the x-coordinates.

• Search and insert. The algorithms for search and insert are similar to those for BSTs, but at the root we use the x-coordinate (if the point to be inserted has a smaller x-coordinate than the point at the root, go left; otherwise go right); then at the next level, we use the y-coordinate (if the point to be inserted has a smaller y-coordinate than the point in the node, go left; otherwise go right); then at the next level the x-coordinate, and so forth.

insert (0.7, 0.2)	insert (0.5, 0.4)	insert (0.2, 0.3)	insert (0.4, 0.7)	insert (0.9, 0.6)

• Draw. A 2d-tree divides the unit square in a simple way: all the points to the left of the root go in the left subtree; all those to the right go in the right subtree; and so forth, recursively. Your draw() method should draw all of the points to standard draw in black and the subdivisions in red (for vertical splits) and blue (for horizontal splits). This method need not be efficient—it is primarily for debugging.

The prime advantage of a 2d-tree over a BST is that it supports efficient implementation of range search and nearest neighbor search. Each node corresponds to an axis-aligned rectangle in the unit square, which encloses all of the points in its subtree. The root corresponds to the unit square; the left and right children of the root corresponds to the two rectangles split by the x-coordinate of the point at the root; and so forth.

• Range search. To find all points contained in a given query rectangle, start at the root and recursively search for points in both subtrees using the following pruning rule: if the query rectangle does not intersect the rectangle corresponding to a node, there is no need to explore that node (or its subtrees). A subtree is searched only if it might contain a point contained in the query rectangle.

• Nearest neighbor search. To find a closest point to a given query point, start at the root and recursively search in both subtrees using the following pruning rule: if the closest point discovered so far is closer than the distance between the query point and the rectangle corresponding to a node, there is no need to explore that node (or its subtrees). That is, a node is searched only if it might contain a point that is closer than the best one found so far. The effectiveness of the pruning rule depends on quickly finding a nearby point. To do this, organize your recursive method so that when there are two possible subtrees to go down, you choose first the subtree that is on the same side of the splitting line as the query point; the closest point found while exploring the first subtree may enable pruning of the second subtree.

Clients.  You may use the following interactive client programs to test and debug your code.

• KdTreeVisualizer.java computes and draws the 2d-tree that results from the sequence of points clicked by the user in the standard drawing window.

• RangeSearchVisualizer.java reads a sequence of points from a file (specified as a command-line argument) and inserts those points into a 2d-tree. Then, it performs range searches on the axis-aligned rectangles dragged by the user in the standard drawing window.

• NearestNeighborVisualizer.java reads a sequence of points from a file (specified as a command-line argument) and inserts those points into a 2d-tree. Then, it performs nearest neighbor queries on the point corresponding to the location of the mouse in the standard drawing window.

Analysis of running time and memory usage. Analyze the effectiveness of your approach to this problem by giving estimates of its time and space requirements.

• Give the total memory usage in bytes (using tilde notation) of your 2d-tree data structure as a function of the number of points N, using the memory-cost model from lecture and Section 1.4 of the textbook. Count all memory that is used by your 2d-tree, including memory for the nodes, points, and rectangles. For the purposes of this assignment, assume that each Point2D object uses 32 bytes.

• Give the expected running time in seconds (using tilde notation) to build a 2d-tree on N uniformly random points in the unit square. (Do not count the time to read in or generate the points.) Using the given input files is not sufficient.

• How many nearest neighbor calculations can your 2d-tree implementation perform per second for input100K.txt (100,000 points) and input1M.txt (1 million points), where the query points are uniformly random points in the unit square? (Do not count the time to read in the points or to build the 2d-tree.) Repeat this question but with the brute-force implementation.

Submission.  Submit only PointSET.java and and KdTree.java. Each of the two data types should include their own main() that thoroughly tests the associated operations. We will supply Point2D.java, RectHV.java, stdlib.jar, and algs4.jar. You may not call any library functions other than those in java.lang, java.util, stdlib.jar, and algs4.jar. Finally, submit a readme.txt file and answer the questions.

Challenge for the bored.  Create a convincing boid simulator using a kdTree to track boids. You'll need to add a new method called kNearest that returns each boid's k nearest neighbors. Feel free to use the (uncommented and hacked together) starter code provided on the ftp site. It's not too hard to get my starter code running (and it looks cool), but the flocking really isn't quite there (e.g. boids seem to like to stay precisely evenly spaced), and the hawk manuevers like a brick (largely due to my physics model where the hawk gets a fixed amount of directional thrust. If you make the delta thurst large enough to allow manueverability, then he can outrun any boid, which is no fun). Josh is the only one who will provide support for this optional part of the assignment. Working simulations should be emailed directly to Josh. Very good submissions that substantially improve the overall flocking behavior will earn a single point of extra credit. Code that simply fills in the blanks in BoidKdTree will not get extra credit (but still feel free to email me with such submissions along with any thoughts you may have on this challenge). Due by Dean's date.