| Name and Description | N = 1 | N = 2 | N = 3 | N = 4 | N = 5 |
|---|---|---|---|---|---|
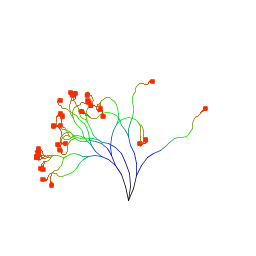
| Joonas Govenius The program draws "flowers". N is used to determine the number of branches from the root. An arbitrary formula (1.9 * 1.3^N) is used to give a nice range of values for 0 <= N <= 7. Each branch has curling, a change of colors, and a bigger radius for the leaves (flowers). |
 |
 |
 |
 |
 |
| Evan Jeng I first picked the shape hexagon and began inlaying each hexagon 3 smaller hexagons. Then, I decided to split each hexagon into 3 component rhombuses. Using black, gray, and white, I found that I could create a visual effect of many 3D cubes. But in the end, I decided on alternating layers between 2 different color schemes and it looks rather nice. Interestingly, it converges to sierpinski's triangle as well. |
 |
 |
 |
 |
 |
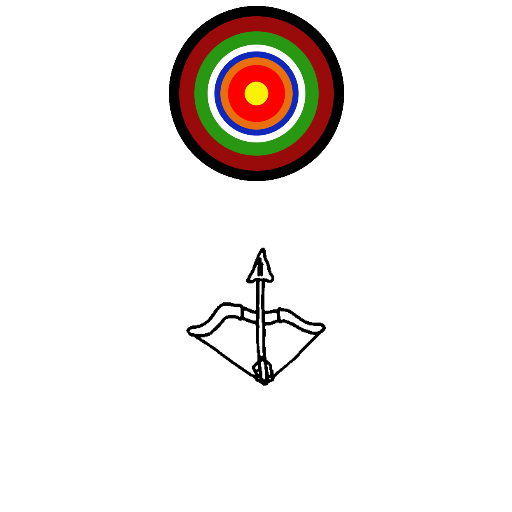
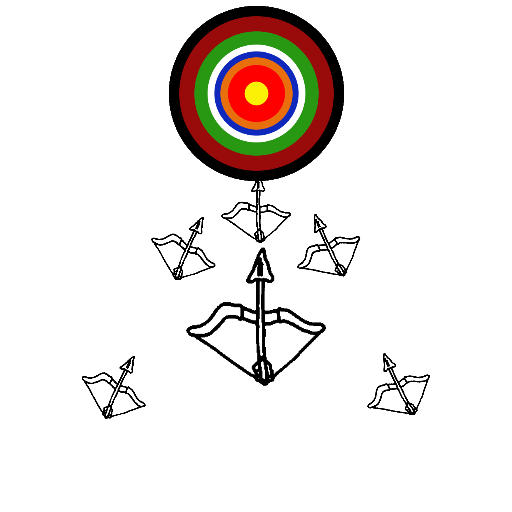
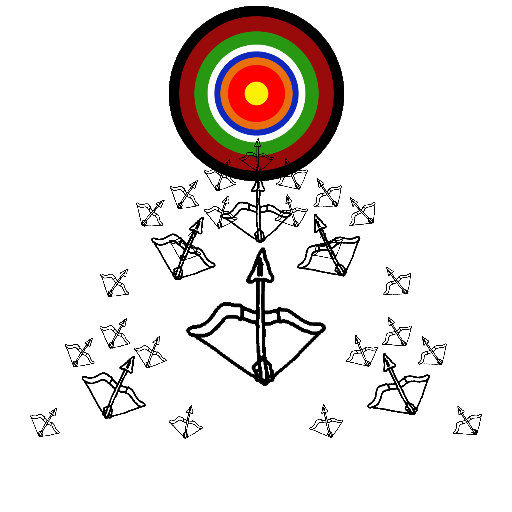
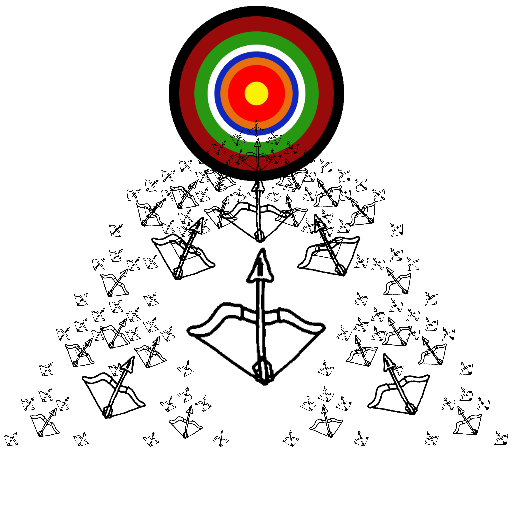
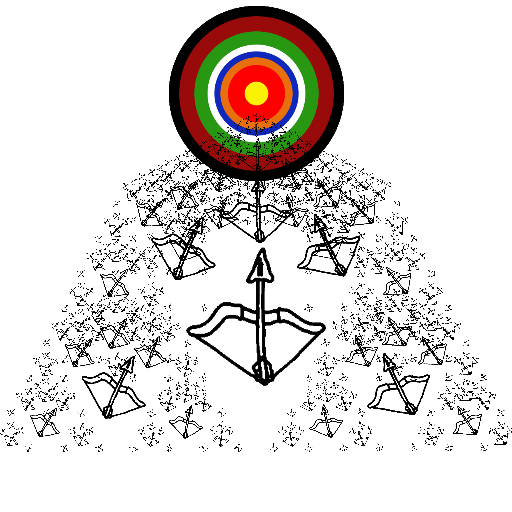
| Gregory Mayer My artistic program uses gifs to create a recursive pattern of bows and arrows, all of which point towards a bullseye. The program creates 5 arrows around its parent arrow, using the Math.atan function, so that they would all point towards a specified point (the point where the bullseye is located). |
 |
 |
 |
 |
 |
| Shuo Zhang Each circle spawns two circles, one at 0 degrees and one 30 degrees, making an "arm". These angles are relative to the direction that the circle is "facing," which makes them spiral. I used basic trig calculations. Each of three arms are each set off 120 degrees from the others. Finally I took a screen shot of the image and ran it through some filters in Photoshop. I used the resulting image as the background. |
 |
 |
 |
 |
 |
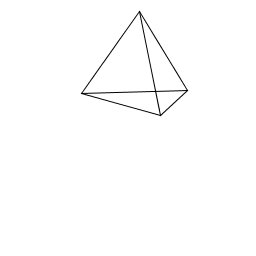
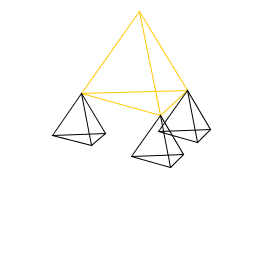
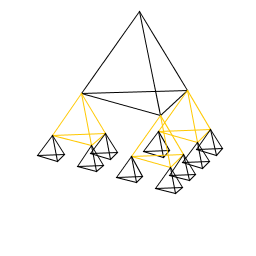
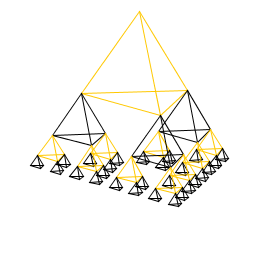
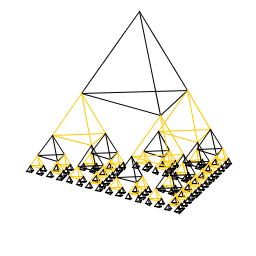
| Doug Eshleman My Art.java program creates a 3D pyramid and then makes a smaller pyramid at each of the bottom corners. |
 |
 |
 |
 |
 |
| Maria Phillip My creation draws a fractal pattern of hearts. I made a function that drew one heart based on an input size. |
 |
 |
 |
 |
 |
| Michael Wu My program draws a fractal fern with a randomized recursive root system. I had the fern color lighten nearer the leaves. The fern initially bends in a random direction, and generates a trunk and 2 branches, with the trunk longer than the branches. The root system starts with one long root, picks a random number between 2 and 5 for successive roots, spread randomly on each side. Subroots are shorter and thinner than parent roots at a set ratio with a small bit of error. They are intermittently spaced along the fern sides with a bit of error also. |
 |
 |
 |
 |
 |
| Scott Henkelman This program will draw two different images, depending on whether the input is odd or even. When the input is odd, it will draw trees receeding into the distance (as N increases), as well as clouds creating a similar but opposite effect in a daytime sky. For even inputs the image is similar, except it is a nitetime sky with stars in the same pattern as the coulds. Each recursion creates a new row of trees/stars/clouds closer to the horizon as well as smaller. |
 |
 |
 |
 |
 |
| Ragnhild Lunnan My artistic creation was inspired by a drawing at: http://www.geocities.com/CollegePark/Lab/2276/Page4.gif. It vaguely resembled a Norwegian flag. I first drew a blue square, then draw four smaller white squares on top of it, and finally four smaller red squares, but afterwards I realized there was another way. |
 |
 |
 |
 |
 |
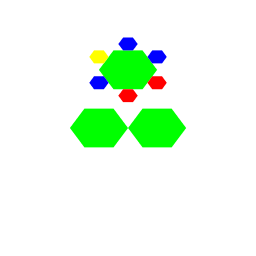
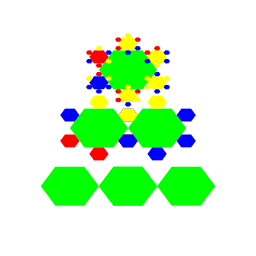
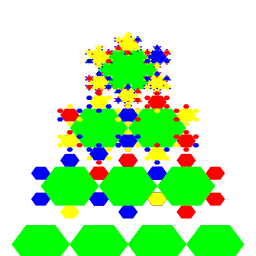
| Carly Sakumura For my artistic program I created a "Christmas Tree" with hexagons, the center one set at green, and then the outer ones set at random colors. This function was called recursively to increase the number of hexagons, and then called recursively again to form a triangle of hexagons, giving it the effect of a christmas tree with red, yellow and blue lights. |
 |
 |
 |
 |
 |
| Nathan Buch My Art program produces a seemingly-random collection of bubbles centered around the image of a bar of soap. A large bubble is drawn followed by progressively smaller bubbles, each centered at a point on the edge of the previous bubble. This gives the perception that the bubbles are "sticking" to each other. Every every increase in N yields more bubbles surrounding each larger bubble. Some tweaks were added to make the final image look more realistic (along with the addition of two intersecting arcs on each bubble to simluate light reflecting off the surface). |
 |
 |
 |
 |
 |
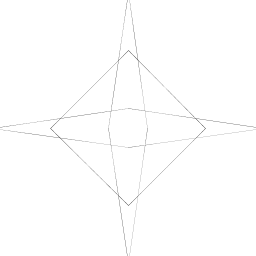
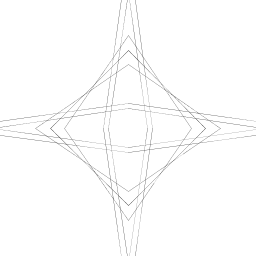
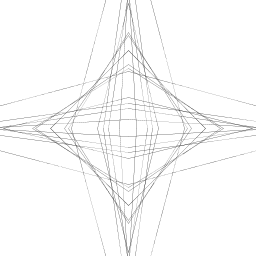
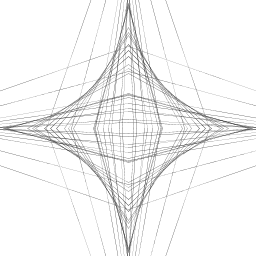
| Eric Schlossberg My artistic creation takes an initial line of (.5*xaxis, 0), (0, .5 * yaxis) and finds two lines around it. One is halfway closer to the origin on the x axis pt, but halfway away from its origin by the y axis. The second is the other way around. Each of these 2 lines have 2 lines of their own half of its distance from the original line to and away from the origin. All of the lines are touching both the x and y axis (in its standard form of x1, y2 = 1 and x2, y1 = 0). The higher the order, the more lines created per each line so it appears more complex. The creation goes from looking like 1 line (in each region) to a smooth curve (at order 9). |
 |
 |
 |
 |
 |
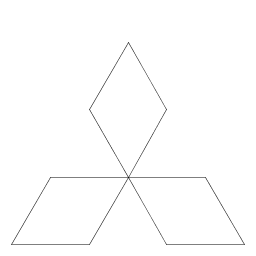
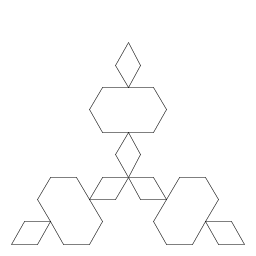
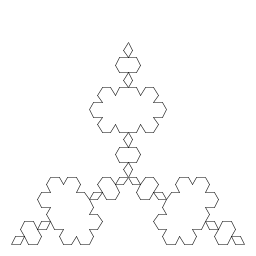
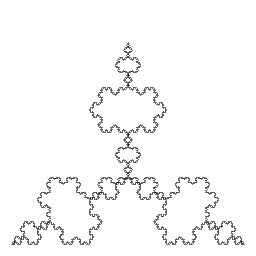
| George Brell I wrote a program that applies the koch anti-snowflake pattern to an equilateral triangle. (The bottom of the picture doesn't show well on some browsers.) |
 |
 |
 |
 |
 |
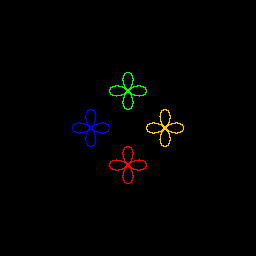
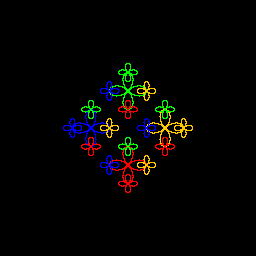
| John Chang My artistic program is a play on Anthony Soroka's creation from Fall '06. I have a similar rose curve parametrized by x = r*cos(theta)*cos(2*theta) and y = r*sin(theta)*cos(2* theta). For both n=0 and n=1, I have an empty graph. For n=1, a rose curve actually is graphed, but it is black. It is blank so that the color of the main rose curve doesn't bias the final drawing. There is a method which loops to draw 4 different colors. |
 |
 |
 |
 |
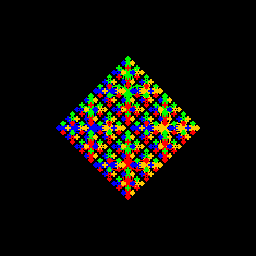 |
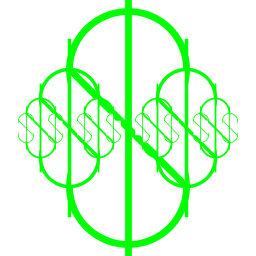
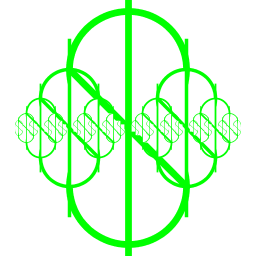
| Ryan Truchelut My art program is a series of recurring dollar signs. Instead of using StdDraw.arc() to draw semicircles, I drew full circles and then drew a white rectangle that erased the unwanted halves. |
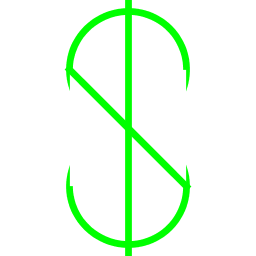 |
 |
 |
 |
 |
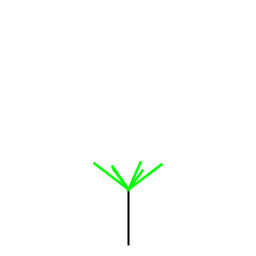
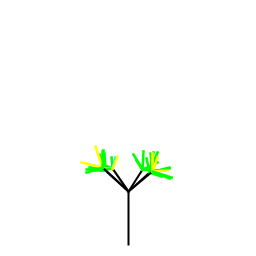
| T.J. Fazio Basically, my program draws a tree. Two branches extend from each branch at a set angle with some randomness to the angles and lengths of the branches. I also added some local symmetry requirements on the random angles and lengths without allowing pairs to be PERFECTLY symmetric. Then, to spice up the leaves (lower depth) of the drawing, I added an argument for the number of pairs of branches to sprout from each tree. N between (1-5) gets three pairs, while (6-8) works with two pairs, |
 |
 |
 |
 |
 |
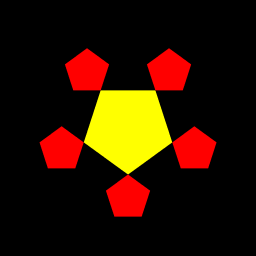
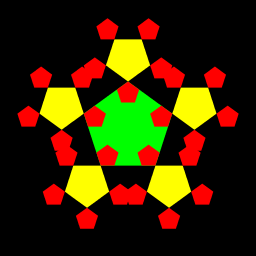
| Chris Thompson Art draws a pentagon and recursively draws a half-sized, inverted pentagon at each vertex for N iterations. It draws an initial pentagon, then designates the center points a distance of 3r/2 from the center of the previous iteration. I then added an if statement to each function: one that would flip the pentagon every other iteration in draw, and one that would flip the positions accordingly in fractal. |
 |
 |
 |
 |
 |
| Sheng Xu I created a pattern resembling a windmill with four leaves and four half-sized windmills residing on each tip of every leaf with alternating color of red and pink. |
 |
 |
 |
 |
 |
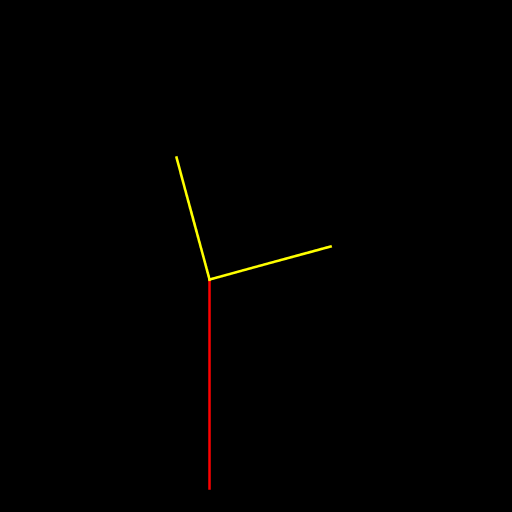
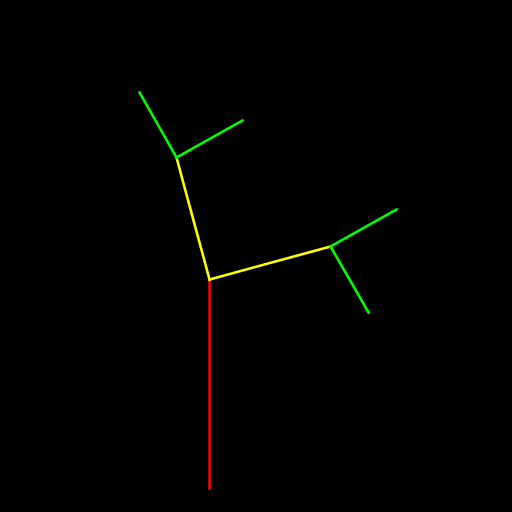
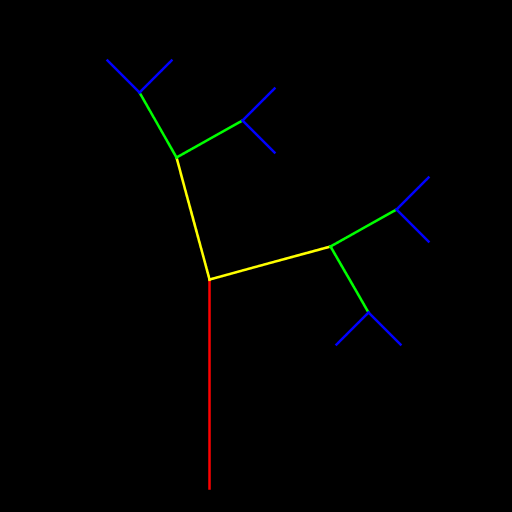
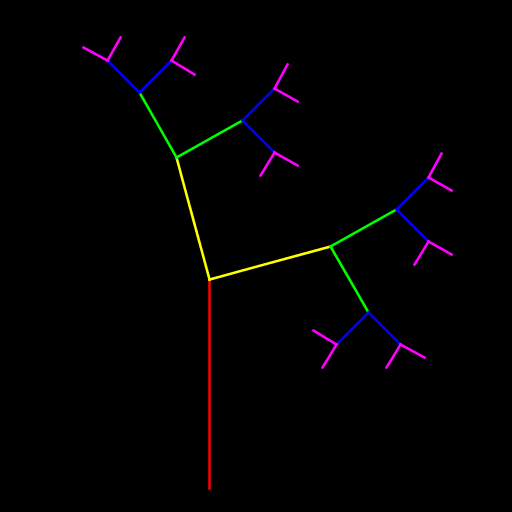
| Katherine Roelofs The program creates a curling tree with N-1 forks. At each fork, one branch goes off to the left at an angle measured clockwise from the vertical and the other branch goes off to the right at the same angle measured clockwise from the horizontal. |
 |
 |
 |
 |
 |
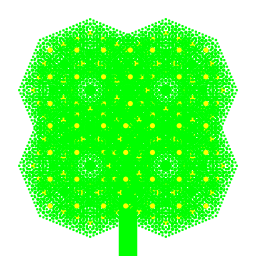
| Laura Keay My artistic creation is a festive four leaf clover for St. Patrick's Day. It looks remarkably realistic because included in the program is a command to draw some yellow spots in, instead of just making the whole thing [unrealistically] green. |
 |
 |
 |
 |
 |
| Trenton Arthur My artistic creation is a series of squares by making 4 different polygons that each make two triangles and when drawn together make a square. I then made each of the polygons randomly select a color. |
 |
 |
 |
 |
 |
| Jaimeson Rice I drew a yellow smiley face with a black arced smile and recursively generated kaleidoscope-esque eyes. |
 |
 |
 |
 |
 |
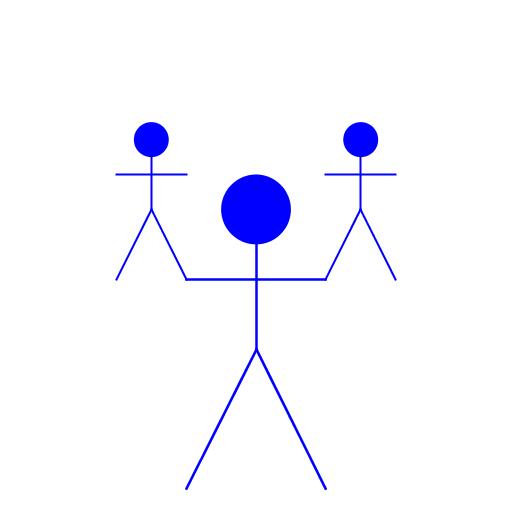
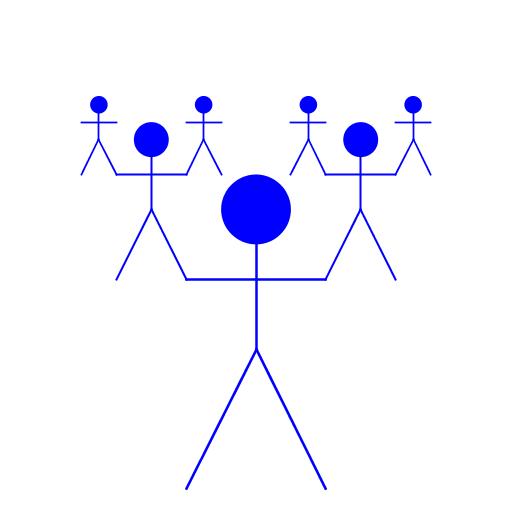
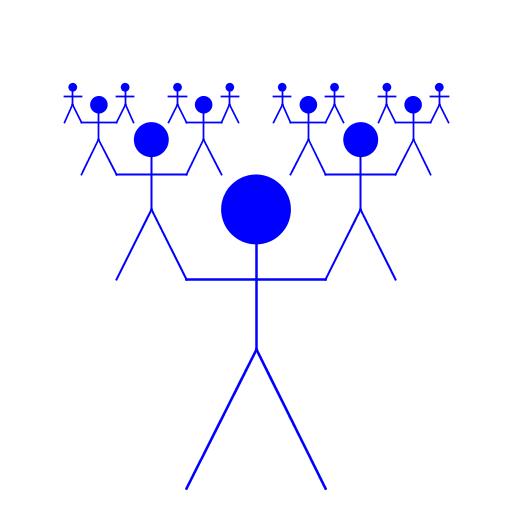
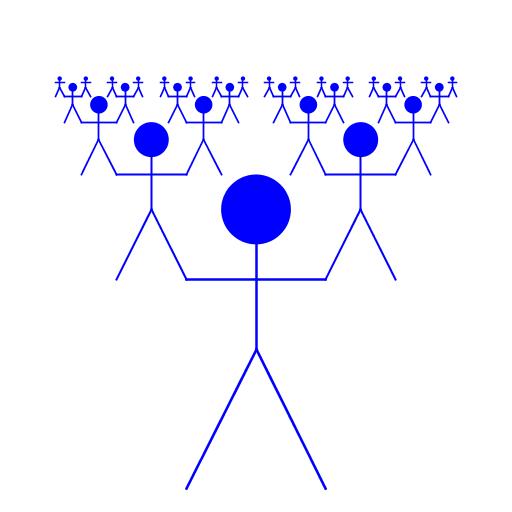
| Michael Koniali My artistic creation is called "Balancing Act." It begins with one stick figure man at the bottom of the screen. Then, from each of his hands he supports another man half his size. They are colored blue in solidarity with Dr. Tobias F|nke and his quest to become a member of the Blue Man Group. |
 |
 |
 |
 |
 |
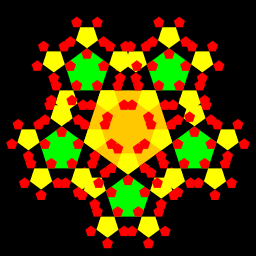
| Hyungjune Kang The program outputs a figure that is formed by several pentagons and stars inside them. When N=1, 6 pentagons and 5 stars appear. One pentagon is centered in the middle, while others share one side of that center pentagon. 5 stars are circumscribed in those 5 pentagons at the bottommost level. To create this figure, I did some messy calculation in order to compute the coordinates of the center of each pentagon, which includes the angle theta=18 degrees and 36 degrees. |
 |
 |
 |
 |
 |
| Igor Dikiy My artistic creation is a tree made up of semicircles. The center of each branch is at the end of the previous branch. |
 |
 |
 |
 |
 |
| Katherine Th My Art program draws a flower out of circles that surround inner circles as petals. Each circle has 8 evenly spaced circles surrounding it, calculated using trig functions. |
 |
 |
 |
 |
 |