The Atomic Nature of Matter

Download Project Zip | Submit to TigerFile

TigerFile Submission Requirements - 20 submission limit

For the final project, there is a limit of twenty (20) times that you may click the Check Submitted Files to receive feedback from the TigerFile auto-grader. If you are working with a partner, this limit applies to the group. This policy is intended to enable timely and constructive feedback on your work while you are programming (but discourage you from relying on the autograder as your exclusive debugging tool).

Getting Started

Download and expand the project zip file for this assignment, which contains the files you will need for this assignment.
Review Section 2.4 in the textbook, especially the part on depth-first search. Finding all the pixels in a blob is similar to finding a percolating path.
This is a partner project. Instructions for help finding a partner and creating a TigerFile group can be found on Ed.
The rules for partnering:
- Choose a partner whose skill level is close to your own - only two partners per group.
- Your partner does not have to be in your precept.
- The rules for partnering are specified on the course syllabus. Make sure you read and understand these rules, and please post on Ed if you have questions. In your acknowledgments.txt file, you must indicate that you adhered to the COS 126 partnering rules.

Historical perspective

The atom played a central role in 20th century physics and chemistry, but prior to 1908 the reality of atoms and molecules was not universally accepted. In 1827, the botanist Robert Brown observed the random erratic motion of microscopic particles suspended within the vacuoles of pollen grains. This motion would later become known as Brownian motion. Einstein hypothesized that this motion was the result of millions of even smaller particles—atoms and molecules—colliding with the larger particles.

In one of his miraculous year (1905) papers, Einstein formulated a quantitative theory of Brownian motion in an attempt to justify the existence of atoms of definite finite size. His theory provided experimentalists with a method to count molecules with an ordinary microscope by observing their collective effect on a larger immersed particle. In 1908 Jean Baptiste Perrin used the recently invented ultramicroscope to experimentally validate Einstein’s kinetic theory of Brownian motion, thereby providing the first direct evidence supporting the atomic nature of matter. His experiment also provided one of the earliest estimates of Avogadro’s number. For this work, Perrin won the 1926 Nobel Prize in physics.

The problem.

In this project, you will redo a version of Perrin’s experiment. Your job is greatly simplified because with modern video and computer technology—in conjunction with your programming skills—it is possible to accurately measure and track the motion of an immersed particle undergoing Brownian motion. We supply video microscopy data of polystyrene spheres (beads) suspended in water, undergoing Brownian motion. Your task is to write a program to analyze this data, determine how much each bead moves between observations, fit this data to Einstein’s model, and estimate Avogadro’s number.

The data.

We provide ten (10) datasets, obtained by William Ryu using fluorescent imaging. Each dataset is stored in a subdirectory (named run_1 through run_10) and contains a sequence of two hundred (200) 640-by-480 color images (named frame00000.jpg through frame00199.jpg).

Here is a movie of several beads undergoing Brownian motion.

Below is a typical raw image (left) and a cleaned up version (right) using thresholding, as described below.

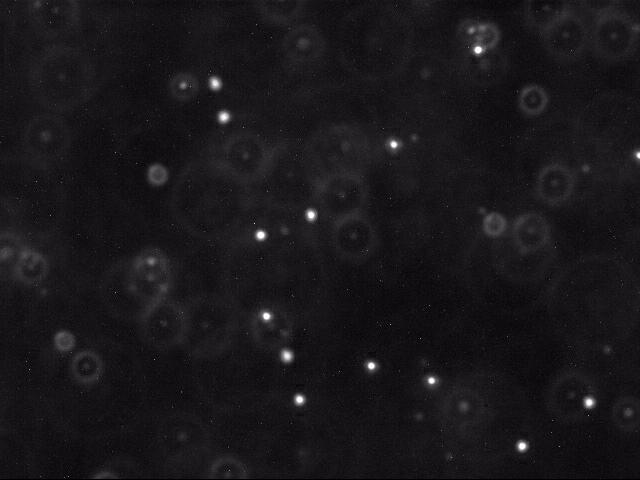Each image shows a two-dimensional cross section of a microscope slide. The beads move in and out of the microscope’s field of view (the $x$- and $y$-directions). Beads also move in the z-direction, so they can move in and out of the microscope’s depth of focus; this results in halos, and it can also result in beads completely disappearing from the image.

I. Particle identification.

The first challenge is to identify the beads amidst the noisy data. Each provided image is 640-by-480 pixels, and each pixel is represented by a Color object which needs to be converted to a luminance value as an intensity ranging from 0.0 (black) to 255.0 (white).

Note: Each supplied image is 640-by-480 pixels, but your solution should be able to accept images of any size.

Whiter pixels correspond to beads (foreground) and blacker pixels to water (background). We break the problem into three pieces: (i) read an image, (ii) classify the pixels as foreground or background, and (iii) find the disc-shaped clumps of foreground pixels that constitute each bead.

Reading the image. Use the Picture data type from Section 3.1 to read the image. By convention, pixels are measured from left-to-right ($x$-coordinate) and top-to-bottom ($y$-coordinate).
Classifying the pixels as foreground or background. We use a simple, but effective, technique known as thresholding to separate the pixels into foreground and background components: all pixels with monochrome luminance values strictly below some threshold tau are considered background; all others are considered foreground. The two pictures above illustrates the original frame (above left) and the same frame after thresholding (above right), using tau = 180.0. An approach for computing luminance is demonstrated in Luminance.java.
Finding the blobs. A polystyrene bead is represented by a disc-like shape of at least some minimum number min (typically 25) of connected foreground pixels. A blob or connected component is a maximal set of connected foreground pixels, regardless of its shape or size. We will refer to any blob containing at least min pixels as a bead. The center of mass of a blob (or bead) is the average of the $x$- and $y$-coordinates of its constituent pixels.

Create a helper data type Blob that has the following API.

   public class Blob {
        //  creates an empty blob
        public Blob()                          

        //  adds pixel (x, y) to this blob
        public void add(int x, int y)          

        //  number of pixels added to this blob
        public int mass()                      

        //  Euclidean distance between the center of masses of the two blobs
        public double distanceTo(Blob that)    

        //  string representation of this blob (see below)
        public String toString()               

        //  tests this class by directly calling all instance methods
        public static void main(String[] args) 
}

String representation. The toString() method returns a string containing the blob’s mass; followed by whitespace; followed by the $x$- and $y$-coordinates of the blob’s center of mass, enclosed in parentheses, separated with a comma, and using four digits of precision after the decimal point.

Performance requirement. The constructor and each instance method must take constant time.

Next, write a data type BeadFinder that has the following API. Use a recursive depth-first search to identify the blobs and beads efficiently.

    public class BeadFinder {
        //  finds all blobs in the specified picture using luminance threshold tau
        public BeadFinder(Picture picture, double tau)

        //  returns all beads (blobs with >= min pixels)
        public Blob[] getBeads(int min)

        //  test client, as described below
        public static void main(String[] args)
    }

The main() method takes an integer min, a floating-point number tau, and the name of an image file as command-line arguments; create a BeadFinder object using a luminance threshold of tau; and print all beads (blobs containing at least min pixels), as shown here:

java-introcs BeadFinder 0 180.0 run_1/frame00001.jpg
29 (214.7241,  82.8276)
36 (223.6111, 116.6667)
 1 (254.0000, 223.0000)
42 (260.2381, 234.8571)
35 (266.0286, 315.7143)
31 (286.5806, 355.4516)
37 (299.0541, 399.1351)
35 (310.5143, 214.6000)
31 (370.9355, 365.4194)
28 (393.5000, 144.2143)
27 (431.2593, 380.4074)
36 (477.8611,  49.3889)
38 (521.7105, 445.8421)
35 (588.5714, 402.1143)
13 (638.1538, 155.0000)

java-introcs BeadFinder 25 180.0 run_1/frame00001.jpg
29 (214.7241,  82.8276)
36 (223.6111, 116.6667)
42 (260.2381, 234.8571)
35 (266.0286, 315.7143)
31 (286.5806, 355.4516)
37 (299.0541, 399.1351)
35 (310.5143, 214.6000)
31 (370.9355, 365.4194)
28 (393.5000, 144.2143)
27 (431.2593, 380.4074)
36 (477.8611,  49.3889)
38 (521.7105, 445.8421)
35 (588.5714, 402.1143)

In the sample frame, there are fifteen (15) blobs, thirteen (13) of which are beads.

Note: The order in which beads are printed will be dependent upon the type of data structure used to store the blobs and also how an images is traversed, i.e., row major or column major order.

II. Particle tracking.

The next step is to determine how far a bead moves from one time $t$ to the next time $t + Δt$. For our data, there are $Δt = 0.5$ seconds between frames. Assume the data is such that each bead moves a relatively small amount and that beads never collide with one another. (You must, however, account for the possibility that the bead disappears from the frame, either by departing the microscope’s field of view in the $x$- or $y$- direction, or moving out of the microscope’s depth of focus in the $z$-direction.) Thus, for each bead at time $t + Δt$, calculate the closest bead at time $t$ (in Euclidean distance) and identify these two as the same bead. However, if the distance is too large—greater than delta pixels—assume that one of the beads has either just begun or ended its journey.

Next, write a main() method in BeadTracker.java that takes an integer min, a double value tau, a double value delta, and a sequence of image filenames as command-line arguments; identifies the beads (using the specified values for min and tau) in each image (using BeadFinder); and prints the distance that each bead moves from one frame to the next (assuming that distance is no longer than delta). You will do this for beads in each pair of consecutive frames, printing each distance that you discover, one after the other.

java-introcs BeadTracker 25 180.0 25.0 run_1/*.jpg
7.1833
4.7932
2.1693
5.5287
5.4292
4.3962
...

Note: with this procedure, there is no need to build a data structure that tracks an individual bead through a sequence of frames.

III. Data analysis.

Einstein’s theory of Brownian motion connects microscopic properties (e.g., radius, diffusivity) of the beads to macroscopic properties (e.g., temperature, viscosity) of the fluid in which the beads are immersed. This amazing theory enables us to estimate Avogadro’s number with an ordinary microscope by observing the collective effect of millions of water molecules on the beads.

Estimating the self-diffusion constant. The self-diffusion constant D characterizes the stochastic movement of a molecule (bead) through a homogeneous medium (the water molecules) as a result of random thermal energy. The Einstein–Smoluchowski equation states that the random displacement of a bead in one dimension has a Gaussian distribution with mean zero and variance $σ^2 = 2 D Δt$, where $Δt$ is the time interval between position measurements. That is, a molecule’s mean displacement is zero and its mean square displacement is proportional to the elapsed time between measurements, with the constant of proportionality $2*D$. We estimate $σ^2$ by computing the variance of all observed bead displacements in the $x$- and $y$-directions. Let $(Δx_1, Δy_1), \ldots, (Δx_n, Δy_n)$ be the $n$ bead displacements, and let $r_1, \ldots, r_n$ denote the radial displacements. Then $$ σ^2 = \frac{(Δx^2_1+…+Δx^2_n)+(Δy^2_1+\ldots+Δy^2_n)}{2n} = \frac{r^2_1+\ldots+r^2_n}{2n} $$

For our data, $Δt = 0.5$, so $σ^2$ is an estimate for $D$ as well.

Note that the radial displacements in the formula above are measured in meters. The radial displacements output by your BeadTracker program are measured in pixels. To convert from pixels to meters, multiply by $0.175 × 10^{−6}$ (meters per pixel).
Estimating the Boltzmann constant. The Stokes–Einstein relation asserts that the self-diffusion constant of a spherical particle immersed in a fluid is given by

$$ D = \frac{kT}{6π\eta\rho} $$

where, for our data,
- $T$ = absolute temperature = $297$ Kelvin (room temperature);
- $\eta$ = viscosity of water at room temperature = $ 9.135 × 10^{−4} N·s·m^{−2} $;
- $\rho$ = radius of bead = $0.5 × 10^{−6}$ meters; and
- $k$ is the Boltzmann constant.

All parameters are given in SI units. The Boltzmann constant is a fundamental physical constant that relates the average kinetic energy of a molecule to its temperature. We estimate $k$ by measuring all of the parameters in the Stokes–Einstein equation, and solving for $k$.

Estimating Avogadro’s number. Avogadro’s number $N_A$ is defined to be the number of particles in a mole. By definition, $k = R / N_A$, where the universal gas constant $R$ is approximately $8.31446$. Use $R / k$ as an estimate of Avogadro’s number.

For the final part, write Avogadro.java with a main() that reads the radial displacements $r_1, r_2, r_3, \ldots$ from standard input and estimates Boltzmann’s constant and Avogadro’s number using the formulas described above.

more displacements-run_1.txt
 7.1833
 4.7932
 2.1693
 5.5287
 5.4292
 4.3962
...

java-introcs Avogadro < displacements-run_1.txt
Boltzmann = 1.2535e-23
Avogadro  = 6.6329e+23

java-introcs BeadTracker 25 180.0 25.0 run_1/*.jpg | java-introcs Avogadro
Boltzmann = 1.2535e-23
Avogadro  = 6.6329e+23

Output format.

Use four digits of precision after the decimal point, both in BeadTracker and Avogadro.

FAQ.

My answers match the reference answers, except sometimes they are off by 0.0001. Why could cause this? It is likely a combination of floating-point roundoff error and printing only four (4) digits after the decimal point. For example, this discrepancy can arise if one solution computes the value 0.12345 (which gets rounded up to 0.1235) and another computes the value 0.1234499999999 (which gets rounded down to 0.1234). You need not worry about such discrepancies on this assignment.

Possible Progress Steps.

We provide some additional instructions below. Click on the ► icon to expand some possible progress steps or you may try to solve Atomic without them. It is up to you!

Click to show possible progress steps

Observe that each directory run_1, run_2, …, run_9 contains a sequence of 200 JPEG images. In total, these data files consume 70MB of space. The file beads-run_1.txt lists the beads found in each frame of run_1 (using tau = 180.0 and min = 25). The files displacements-run_1.txt and displacements-run_2.txt are the output of BeadTracker for those runs.
Implement the Blob data type. Do not store all of the individual pixels that comprise a blob; instead, store three values. Two alternatives are:
- number of pixels, $x$-coordinate center of mass, and $y$-coordinate center of mass or
- number of pixels, sum of $x$-coordinates, and sum of $y$-coordinates needed to compute the center of mass.
Recall the main() method is used to write your test client. This is where you should thoroughly test your Blob implementation. For example, create various Blob objects and call the various Blob methods on these objects.
How can I implement the toString() method to format the numbers? Use String.format(). It works like StdOut.printf(), but returns the resulting string instead of printing it. Here is our toString() method in Blob.
```
    public String toString() {
      return String.format("%2d (%8.4f, %8.4f)", mass, cx, cy);
   }
```
See pp. 130–132 of the textbook to learn more about formatted printing.

Which value should distanceTo() return if the mass of one or both blobs is zero? We recommend Double.NaN. Since this corner case is not specified in the API, we will not test it.

What should toString() return if the mass is zero? We recommend returning the value "0 (NaN, NaN)". Since this corner case is not specified in the API, we will not test it.
Implement the BeadFinder data type. This is the most challenging code to implement.
- Review Section 2.4 in the textbook, especially the part on depth-first search. Finding all the pixels in a blob is similar to finding a percolating path.
- Write the constructor to find all of the blobs and initialize the instance variables. Most of the work for the BeadFinder data type will be here.
  - The crux of this part is to write a private recursive method dfs() that locates all of the foreground pixels in the same blob as the foreground pixel (x, y). To do this, use depth-first search:
    - mark pixel (x, y) as in the current blob;
    - then recursively mark all of its foreground neighbors as in the current blob (but do not recur if the pixel has previously been marked or the pixel indices are out-of-bounds).
    - It is up to you to decide which arguments would be useful for the dfs() method.
  - The constructor should call dfs() from each unmarked pixel (x, y). All of the pixels encountered during a single call to dfs() comprise one blob.
- Next, implement the method getBeads(int min) that searches through the blobs and stores all of the beads (blobs that contain at least the specified number of pixels) in a Blob array. The length of the array should be equal to the number of beads. To determine the number of beads, you may find it helpful to implement a private method countBeads(int min) that counts and returns the number of beads.
- Implement a main() method that takes as command-line arguments min, tau, and the name of a JPEG file. The main() method prints the list of beads.
Can I assume that the dimensions of all of the images are 640-by-480 pixels? No, do not hardwire these constants into your program. Use picture.width() and picture.height() for the width and height, respectively.

To compute the luminance of a pixel: First, get the Color value of that pixel. Then, use the approprivate method in Luminance.java (Program 3.1.3) to get the luminance value for that color.

Are diagonal pixels not considered adjacent? Use only the four ordinal neighbors (north, east, south, and west).

Must I print the beads and displacements in the same order as shown in the assignment specification? No, the order is not specified.
- Testing: The initial descrciption of BeadFinder shows the output from running BeadFinder with run_1/frame00001.jpg. Note that the order in which you print the beads is not important. Here are the results for run_1/frame00000.jpg:

java-introcs BeadFinder 0 180.0 run_1/frame00000.jpg
37 (220.0270, 122.8919)
1 (254.0000, 223.0000)
17 (255.4118, 233.8824)
23 (265.8261, 316.4348)
36 (297.8333, 394.5000)
39 (312.3077, 215.8205)
23 (373.0000, 357.1739)
19 (390.8421, 144.8421)
31 (433.7742, 375.4839)
32 (475.5000,  44.5000)
31 (525.2903, 443.2903)
24 (591.0000, 399.5000)
35 (632.7714, 154.5714)

java-introcs BeadFinder 25 180.0 run_1/frame00000.jpg
37 (220.0270, 122.8919)
36 (297.8333, 394.5000)
39 (312.3077, 215.8205)
31 (433.7742, 375.4839)
32 (475.5000,  44.5000)
31 (525.2903, 443.2903)
35 (632.7714, 154.5714)

java-introcs BeadFinder 0 180.0 run_6/frame00010.jpg
 1 ( 25.0000, 373.0000)
 1 ( 26.0000, 372.0000)
 1 ( 27.0000, 373.0000)
 1 ( 29.0000, 369.0000)
63 ( 34.2063,  32.3175)
 9 ( 97.0000, 341.0000)
65 (141.4615,  54.0615)
70 (165.8571, 165.2857)
60 (173.5667, 200.5333)
50 (198.7000, 113.0200)
 1 (254.0000, 223.0000)
89 (276.9101, 306.6629)
24 (296.3750,  82.9583)
62 (306.6774, 474.6774)
59 (339.1356,  81.5932)
68 (358.9706, 159.0588)
40 (397.0750,  39.2000)
86 (573.3488, 427.0581)
51 (611.7451, 143.8235)
53 (636.1132, 230.6038)
14 (634.5000, 421.7143)
26 (636.5000,  35.0000)

java-introcs BeadFinder 25 180.0 run_6/frame00010.jpg
63 ( 34.2063,  32.3175)
65 (141.4615,  54.0615)
70 (165.8571, 165.2857)
60 (173.5667, 200.5333)
50 (198.7000, 113.0200)
89 (276.9101, 306.6629)
62 (306.6774, 474.6774)
59 (339.1356,  81.5932)
68 (358.9706, 159.0588)
40 (397.0750,  39.2000)
86 (573.3488, 427.0581)
51 (611.7451, 143.8235)
53 (636.1132, 230.6038)
26 (636.5000,  35.0000)

Implement the BeadTracker client.
- The main() method in BeadTracker takes an arbitrary number of command-line arguments, args[0], args[1], and so forth.
- You need to consider only two frames at a time, so do not store all of the frames at the same time.
Use the Picture data type to read a JPEG file.

What should I do if several of the beads in frame t+1 have the same bead in frame t as their closest bead? That happens only rarely, so you should not worry about it—just let the bead in frame t get paired a second time.

I am able to find beads and blobs correctly, but my BeadTracker gives a few errors, despite that it is mostly working. Why could this be?
- Check that, for each bead in frame t + 1, you are finding the closest bead in frame t, and not vice versa.
- Be sure to discard distances greater than delta, not greater than or equal to delta.
Why do I have to compare each bead in frame t + 1 to each bead in frame t? Why can’t I do it the other way around? It is an arbitrary choice, but one that you must follow because it is prescribed in the assignment specification.

Can I assume that all of the runs consist of 200 frames? No, do not hardwire 200 into your program. Use args.length for the number of command-line arguments.

How can I specify 200 image names on the command line? One way is to type them all in.
```
java-introcs BeadTracker 25 180.0 25.0 run_1/frame00000.jpg run_1/frame00001.jpg run_1/frame00002.jpg ...
```
An easier alternative is to use the wildcard capability of the terminal. For example, the following specifies (in alphabetical order) all .jpg files in the run_1 directory.
```
java-introcs BeadTracker 25 180.0 25.0 run_1/*.jpg
```
- Testing: For reference, displacements-run_1.txt, displacements-run_2.txt, and displacements-run_6.txt contain a list of all of the displacements (using tau = 180.0 and min = 25) for run_1, run_2, and run_6, respectively. They were obtained by running

java-introcs BeadTracker 25 180.0 25.0 run_1/*.jpg
7.1833
4.7932
2.1693
5.5287
5.4292
4.3962
...

java-introcs BeadTracker 25 180.0 25.0 run_2/*.jpg
5.1818
7.6884
6.7860
6.4907
4.2102
1.1412
4.4724
7.5191
3.0659
4.4238
5.0600
1.7280
...

java-introcs BeadTracker 25 180.0 25.0 run_6/*.jpg
11.1876
12.4269
10.3113
 1.3954
 3.3196
 0.4732
 1.7367
 3.0060
 4.6087
 1.3282

Implement the Avogadro client.
- The main() method in Avogadro reads a sequence of floating-point numbers from standard input and prints the estimate of Avogadro’s number using the formulas provided in the assignment.
- To calculate $σ^2$, use the second formula listed with radial displacements; these are the results from BeadTracker.
How accurate of an estimate should I get? You should get within 10% or so of the exact value for Avogadro’s number $6.022142 × 10^{23}$. The standard deviation of the radius of the beads is about 10%, so you should not expect results more accurate than this. Your output, however, should agree exactly with ours.

My physics is a bit rusty. Do I need to worry about converting units? Not much, since all of the constants are in SI units. The only conversion you should need to do is to convert from distances measured in pixels (the radial displacements) to distances measured in meters, by using the conversion factor of $0.175 × 10^{−6}$ meters per pixel.

Checkstyle complains about the variables I named T and R. Which names should I use instead? A constant variable (a variable whose value does not change during the execution of a program, or from one execution of the program to the next) should begin with an uppercase letter and use underscores to separate any word boundaries, such as GRAVITATIONAL_CONSTANT. Constant variables should have more meaningful names, such as TEMPERATURE or GAS_CONSTANT.
- Below are the output for displacements-run_1.txt, displacements-run_2.txt, and displacements-run_6.txt.

java-introcs Avogadro < displacements-run_1.txt
Boltzmann = 1.2535e-23
Avogadro  = 6.6329e+23

java-introcs Avogadro < displacements-run_2.txt
Boltzmann = 1.4200e-23
Avogadro  = 5.8551e+23

java-introcs Avogadro < displacements-run_6.txt
Boltzmann = 1.3482e-23
Avogadro  = 6.1670e+23

Perform system testing. As a final test, combine the data collection (BeadTracker) for run_1, run_2, and run_6 with the data analysis (Avogadro). The data for run_2 contains light boundary pixels and run_6 contains pixels whose luminance is exactly 180.0.

java-introcs BeadTracker 25 180.0 25.0 run_1/*.jpg | java-introcs Avogadro
Boltzmann = 1.2535e-23
Avogadro  = 6.6329e+23

java-introcs BeadTracker 25 180.0 25.0 run_2/*.jpg | java-introcs Avogadro
Boltzmann = 1.4200e-23
Avogadro  = 5.8551e+23

java-introcs BeadTracker 25 180.0 25.0 run_6/*.jpg | java-introcs Avogadro
Boltzmann = 1.3482e-23
Avogadro  = 6.1670e+23

Performance Analysis - `readme.txt`.

Formulate a hypothesis for the running time (in seconds) of BeadTracker as a function of the input size $n$ (total number of pixels read in across all frames being processed). Justify your hypothesis in your readme.txt file with empirical data.
Review the lecture and precept exercises for applying the doubling method.
How can I estimate the running time of my BeadTracker program? Use the Stopwatch data type from Section 4.1. Remember to remove it and any additional print statements from your submitted version of BeadTracker.java. When you execute BeadTracker, redirect the output to a file to avoid measuring the time to print the output to the terminal. Run BeadTracker with a variety of input sizes which allow you to get good timing data and form a doubling hypothesis.
How can I run BeadTracker with a variety of input sizes? Do not all the runs have 200 frames? They do, but when you are performing timing experiments, you can simply use a subset of them. You can use the wildcard capability of the terminal to run 10 frames, 20 frames, 40 frames, 80 frames, and 160 frames, as follows:

   java-introcs -Xint BeadTracker 25 180.0 25.0 run_1/frame000[0]*.jpg    > temp.txt

   java-introcs -Xint BeadTracker 25 180.0 25.0 run_1/frame000[0-1]*.jpg  > temp.txt

   java-introcs -Xint BeadTracker 25 180.0 25.0 run_1/frame000[0-3]*.jpg  > temp.txt

   java-introcs -Xint BeadTracker 25 180.0 25.0 run_1/frame000[0-7]*.jpg  > temp.txt

   java-introcs -Xint BeadTracker 25 180.0 25.0 run_1/frame000*.jpg run_1/frame001[0-5]*.jpg > temp.txt

Do I need to use the -Xint option? You can try your experiments with or without the -Xint option. Recall, that -Xint turns off Java optimization, so you may get clearer results when you use the doubling method.
How long should BeadTracker take? It depends on the speed of your computer, but processing 200 frames should take around 10 seconds or less without the -Xint option and about two minutes with the -Xint option.
How much memory should my program use? Our program uses less than 5 MB. You will receive a deduction if you use substantially more. The most common way to waste memory is to hold references to an array of Picture objects in BeadTracker instead of only two at a time. You can use the -Xmx option to limit how much memory Java uses: for example, the following command limits the memory available to Java to 5 MB.

   java-introcs -Xint -Xmx5m BeadTracker 25 180.0 25.0 run_1/*.jpg

When I test with a very small luminance threshold, I get a StackOverflowError, but my code works for larger luminance thresholds. What does this mean? Since DFS is recursive, it consumes memory proportional to the height of the function-call tree. If the luminance threshold is small, the blobs can be very big, and the height of the function-call tree may be very large. We will not test your program on inputs with such big blobs. If, however, you are determined to get it to work on such cases, use the command-line option -Xss20m to increase the stack space.

   java-introcs -Xint -Xss20m BeadTracker 25 18.0 25.0 run_1/*.jpg

Submission.

Reminder: For the final project, there is a limit of twenty (20) times that you may click the Check Submitted Files to receive feedback from the TigerFile auto-grader. If you are working with a partner, this limit applies to the group.

Submit to TigerFile : Blob.java, BeadFinder.java, BeadTracker.java and Avogadro.java. (Do not submit: stdlib.jar, Luminance.java, Stack.java, Queue.java, and/or ST.java.) Finally, submit a readme.txt, including the running-time analysis and a completed acknowledgments.txt file.

Grading

Files	Points
Style	10
Blob.java	14
BeadFinder.java	32
BeadTracker.java	22
Avogadro.java	14
readme.txt	8
Total	100

Enrichment.

What is polystyrene? It is an inexpensive plastic that is used in many everyday things including plastic forks, drinking cups, and the case of your desktop computer. Styrofoam is a popular brand of polystyrene foam. Computational biologists use micron size polystyrene beads (also known as microspheres and latex beads) to capture a single DNA molecule, e.g., for a DNA test.

What is the history of measuring Avogadro’s number? In 1811, Avogadro hypothesized that the number of molecules in a liter of gas at a given temperature and pressure is the same for all gases. Unfortunately, he was never able to determine this number that would later be named after him. Johann Josef Loschmidt, an Austrian physicist, gave the first estimate for this number using the kinetic gas theory. In 1873 Maxwell estimated the number of be around $4.3 × 10^{23}$; later Kelvin estimated it to be around $5 × 10^{23}$. Perrin gave the first “accurate” estimate ($6.5–6.8 × 10^{23}$) of, what he coined, Avogadro’s number. The most accurate estimates for Avogadro’s number and Boltzmann’s constant are computed using x-ray crystallography: Avogadro’s number is approximately $6.022142 × 10^{23}$; Boltzmann’s constant is approximately $1.3806503 × 10^{−23}$.

Where can I learn more about Brownian motion? Here’s the Wikipedia entry. You can learn about the theory in ORF 309. It may be the first subject you will be asked about if you interview on Wall Street.

This assignment was created by David Botstein, Tamara Broderick, Ed Davisson, Daniel Marlow, William Ryu, and Kevin Wayne.