| COS 126 N-Body Simulation |
Programming Assignment |
In 1687 Sir Isaac Newton formulated the principles governing the motion of two particles under the influence of their mutual gravitational attraction in his famous Principia. However, Newton was unable to solve the problem for three particles. Indeed, in general, solutions to systems of three or more particles must be approximated via numerical simulations. Your challenge is to write a program to simulate the motion of N particles in the plane, mutually affected by gravitational forces, and animate the results. Such methods are widely used in cosmology, semiconductors, and fluid dynamics to study complex physical systems. Scientists also apply the same techniques to other pairwise interactions including Coulombic, Biot-Savart, and van der Waals.
Program specification. Write a program NBody.java that:
Reading in the universe. The input format is a text file that contains the information for a particular universe (in SI units). The first value is an integer N which represents the number of particles. The second value is a real number R which represents the radius of the universe, used to determine the scaling of the drawing window. Finally, there are N rows, and each row contains 6 values. The first two values are the x- and y-coordinates of the initial position; the next pair of values are the x- and y-components of the initial velocity; the fifth value is the mass; the last value is a String that is the name of an image file used to display the particle. As an example, planets.txt contains data for our own solar system (up to Mars):
% more planets.txt 5 2.50e+11 1.4960e+11 0.0000e+00 0.0000e+00 2.9800e+04 5.9740e+24 earth.gif 2.2790e+11 0.0000e+00 0.0000e+00 2.4100e+04 6.4190e+23 mars.gif 5.7900e+10 0.0000e+00 0.0000e+00 4.7900e+04 3.3020e+23 mercury.gif 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00 1.9890e+30 sun.gif 1.0820e+11 0.0000e+00 0.0000e+00 3.5000e+04 4.8690e+24 venus.gif
You should read in exactly as many rows of body information as are indicated by N, the first value in the file.
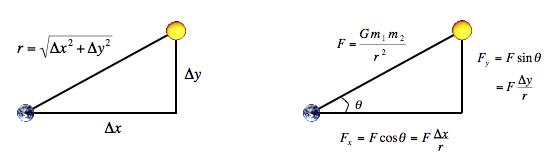
Simulating the universe: the physics. We review the equations governing the motion of the particles, according to Newton's laws of motion and gravitation. Don't worry if your physics is a bit rusty; all of the necessary formulas are included below. We'll assume for now that the position (px, py) and velocity (vx, vy) of each particle is known. In order to model the dynamics of the system, we must know the net force exerted on each particle.

Simulating the universe: the numerics. We use the leapfrog finite difference approximation scheme to numerically integrate the above equations: this is the basis for most astrophysical simulations of gravitational systems. In the leapfrog scheme, we discretize time, and update the time variable t in increments of the time quantum Δt (measured in seconds). We maintain the position (px, py) and velocity (vx, vy) of each particle at each time step. The steps below illustrate how to evolve the positions and velocities of the particles.
Creating an animation. Draw each particle at its current position using standard drawing, and repeat this process at each time step until a designated stopping time. By displaying this sequence of snapshots (or frames) in rapid succession, you will create the illusion of movement. After each time step (i) draw the background image starfield.jpg, (ii) redraw all the bodies in their new positions, and (iii) control the animation speed (about 40 frames per second looks good). You will use several methods from the StdDraw library; click here to see a summary of what this library contains.
Optional finishing touch. For a finishing touch, play the theme to 2001: A Space Odyssey using StdAudio and the file 2001.mid. It's a one-liner using the method StdAudio.play(). If you have trouble doing this, make sure you note it in your readme.txt.
Compiling and executing your program.
(As the checklist explains, you may need to use java and javac in place of java-introcs and javac-introcs depending on your machine's setup.)
To compile your program from the command line, type:
% javac-introcs NBody.java
in your terminal application (e.g., Command Prompt or Terminal). To execute your program from the command line, redirecting from the file planets.txt to standard input, type:
% java-introcs NBody 157788000.0 25000.0 < planets.txt
After the animation stops, your program should output the final state of the universe in the same format as the input, e.g.:Your browser can not display this movie.
Be sure that Javascript is enabled and that you have Flash 9.0.124 or better.
5 2.50e11 1.4925e+11 -1.0467e+10 2.0872e+03 2.9723e+04 5.9740e+24 earth.gif -1.1055e+11 -1.9868e+11 2.1060e+04 -1.1827e+04 6.4190e+23 mars.gif -1.1708e+10 -5.7384e+10 4.6276e+04 -9.9541e+03 3.3020e+23 mercury.gif 2.1709e+05 3.0029e+07 4.5087e-02 5.1823e-02 1.9890e+30 sun.gif 6.9283e+10 8.2658e+10 -2.6894e+04 2.2585e+04 4.8690e+24 venus.gif
Getting started.
Before you begin coding, do the following:
StdDraw.picture(x, y, filename)).
Submission. Submit NBody.java and a completed readme.txt file.
Extra credit. Submit an alternate universe (in our input format) along with the necessary image files. (Only .txt files will be accepted, not .java files.) Describe it in your readme.txt. If its behavior is sufficiently interesting, we'll award extra credit.
Challenge for the bored.
There are limitless opportunities for additional excitement and discovery here.
Try adding other features, such as supporting elastic or inelastic collisions.
Or, make the simulation three-dimensional by doing calculations for x-,
y-, and z-coordinates, then using the z-coordinate
to vary the sizes of the planets.
Add a rocket ship that launches from one planet and has to land on another.
Allow the rocket ship to exert force with the consumption of fuel.