Write a program that simulates the motion of N bodies, mutually affected by gravitational forces, in a two-dimensional space. The time evolution of such systems are usually too complex to compute analytically, but scientists have made significant research contributions (in plasma physics, semiconductors, fluid dynamics and astrophysics) by formulating and simulating appropriate computer models.

This program will be a Java applet similar to the one you did for the warmup. If you have not done the warmup, do it; otherwise you will find it very difficult to complete this assignment. This time, we supply the complete code for the applet class, Nbody.java or NbodyDeluxe.java, and your task is to write a class Body that implement the methods show(), move(), computeForce(), and resetForce(), which are called from the applet. Each Body is characterized by several variables, including: its position x and y (the x and y coordinates), its velocity vx and vy (the x and y components of velocity), its mass m, and the image used to display it. The position and velocity are updated when we compute the effects of mutual gravitational interactions, as described below.

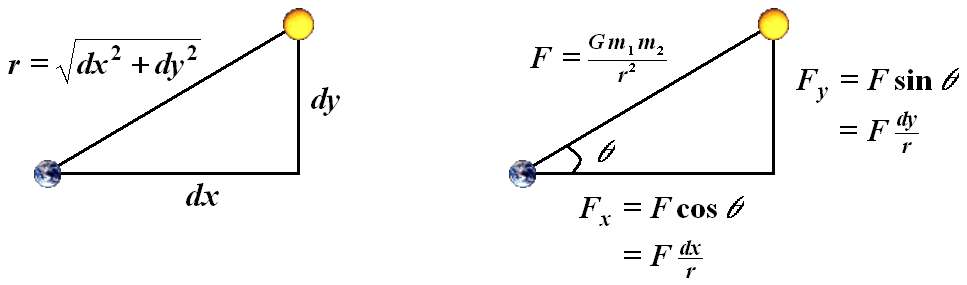
Updating the position and velocity. To update the position and velocity of a Body, you will need to know its acceleration. To determine this, you first have to perform a ``force'' calculation. This requires some elementary physics, which we review now. Don't worry if your physics is a bit rusty; all of the necessary formulas are included below.

• (force calculation) Newton's law of gravitation says that the strength of the gravitational force between two bodies is given by the product of their masses divided by the square of the distance between them, scaled by the gravitational constant G. Note that this is a vector sum: the pull of one body towards another acts on the line between them. Since Java uses Cartesian coordinates to display graphics, it is convenient to break up the gravitational force between two bodies into their x and y components (by projecting the original force onto the x- and y-axes).

  
  

  To calculate the total force acting on one body, you need to accumulate the gravitational force between this body and every other body in the system. The principle of superposition says that the net force acting on a body is the sum of the individual pairwise forces. Thus, by adding up the forces in the x and y directions, we obtain the total forces in the x and y directions.

• (acceleration calculation) Next, use Newton's second law of motion F[ ] = ma[ ] to get the x and y components of the acceleration of each body that is implied by these forces. over the given time quantum dt.

• (discrete simulation) We now describe how to use the above physics equations to update the position and velocity of a body over time. We use the leapfrog finite difference approximation scheme to numerically integrate the above equations: this is the basis for most astrophysical simulations of gravitational systems. In the leapfrog scheme, we discretize time, and increment the time variable t in increments of the time quantum dt. The simulation is more accurate when dt is very small, but requires more computational resources.

  We calculate the position and velocity half a timestep out of phase (which explains the name leapfrog). Interestingly, we do not know the position and velocity at the same time step.

  First, use the position at time t to compute the forces and accelerations.

  Second, use these computed forces to advance the body's velocity from time t - dt/2 to time t + dt/2. The velocity at time t + dt/2 is given by v[ ] = v[ ] + a[ ] dt. The square brackets indicate that these are all vector formulae, e.g., v[ ] represents the x and y coordinates of the velocity.

  Finally, use the these new velocities to update the position at time t + dt. Assume the velocity is held constant in the interval from t to t + dt, and use the formula p[ ] = p[ ] + v[ ] dt.

class Body will be similar to class Ball in many ways, except that now each body has a force associated with it. In the warmup, the velocity of a ball never changes, since there is no external force acting upon it. For a body, after each time quantum, you need to update the position and velocity according to the gravitational interactions. So, each body should have its own position, velocity, force, mass, and image. There should also be a classwide variable double G = 6.67e-11 to represent the universal gravitational constant (in the appropriate units). Remember that it is good programming practice to make all data members within a class private: make it a true ADT by only allowing access through public methods.

• The following constructor should initialize the appropriate quantities and set the initial forces to zero.

  Body(double x, double y, double vx, double vy, double mass, Image image, Applet applet)
  

• Method void move(int dt) updates the position and velocity of a body, using the current velocity and force for an interval of time dt. It is similar to method move in Ball, except that the force causes an acceleration. Also, in Ball we used dt = 1.

• Method void show() displays the graphical image associated with the Body.

• Method void resetForce() is used to reset the force acting on a particular body to zero.

• Method void computeForce(Body b) computes and updates the force acting on a body that is exerted by a second body b, using the physics of mutual gravitational interaction.

class Nbody is similar to MovingBall, and two version are provided to you. Nbody.java is a no frills version; NbodyDeluxe.java adds a graphical user interface. The class Nbody is the client program, and you should use exactly as is. The code below (included in Nbody.java) uses the computeForce method, along with the principle of superposition, to compute the total force acting on a particular body.

        for (i = 0; i < N; i++)
            a[i].resetForce();
        
        for (i = 0; i < N; i++)
            for (j = 0; j < N; j++)
                if (i != j)
                   a[i].computeForce(a[j]);

Extra credit. Try adding other features, such as merging bodies when they collide. Or, make the simulation three-dimensional by doing calculations for x, y, and z coordinates, then using the z coordinate to vary the sizes of the planets. Design a planetary system with interesting behavior.