COS 111 Fall 1999

Solution Set for Assignment 10

Problem 1

Brookshear, Chapter 10 Review Problem 13 (pg 485). Should player X select move A or move B? Why? How does selecting a "production" differ from a one-person game such as the eight-puzzle?

There were two responses to this, but the first is more in the spirit of game-trees in artificial intelligence:
  1. The first player must choose B, even though it at first appears to be a bad move. This is because no matter what player Y does on the next turn, player X can make a move to guarantee a tie.

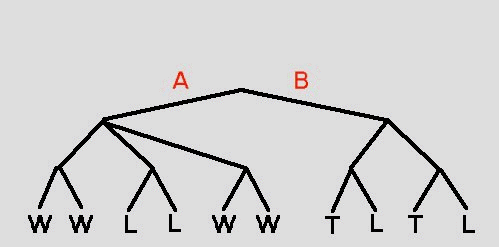
    If player X chose move A, then player Y could (and, presumably, would) chose the middle move, which forces X to lose.

  2. The first player could choose A, if it seems possible that Y will make a mistake on the next move, and player X is willing to gamble on that possibility.

The difference between a multi-player game and a one-player game, such as the 8-puzzle described below, is that when choosing a step in the multi-player game, the player must anticipate the move of another player, who seeks to reduce the player's chances of winning. In the example above, for example, move A would lead to a win, if it weren't for that pesky player Y, and we must consider player Y's possible moves before choosing our own.

Problem 2

Brookshear, Chapter 10 Review Problem 17 (pg 486). Draw the search tree that is generated by a the algorithm of Fig 10.9 in an attempt to solve the eight-puzzle from the following start state, assuming the heuristic used is the same as that developed in section 10.3.

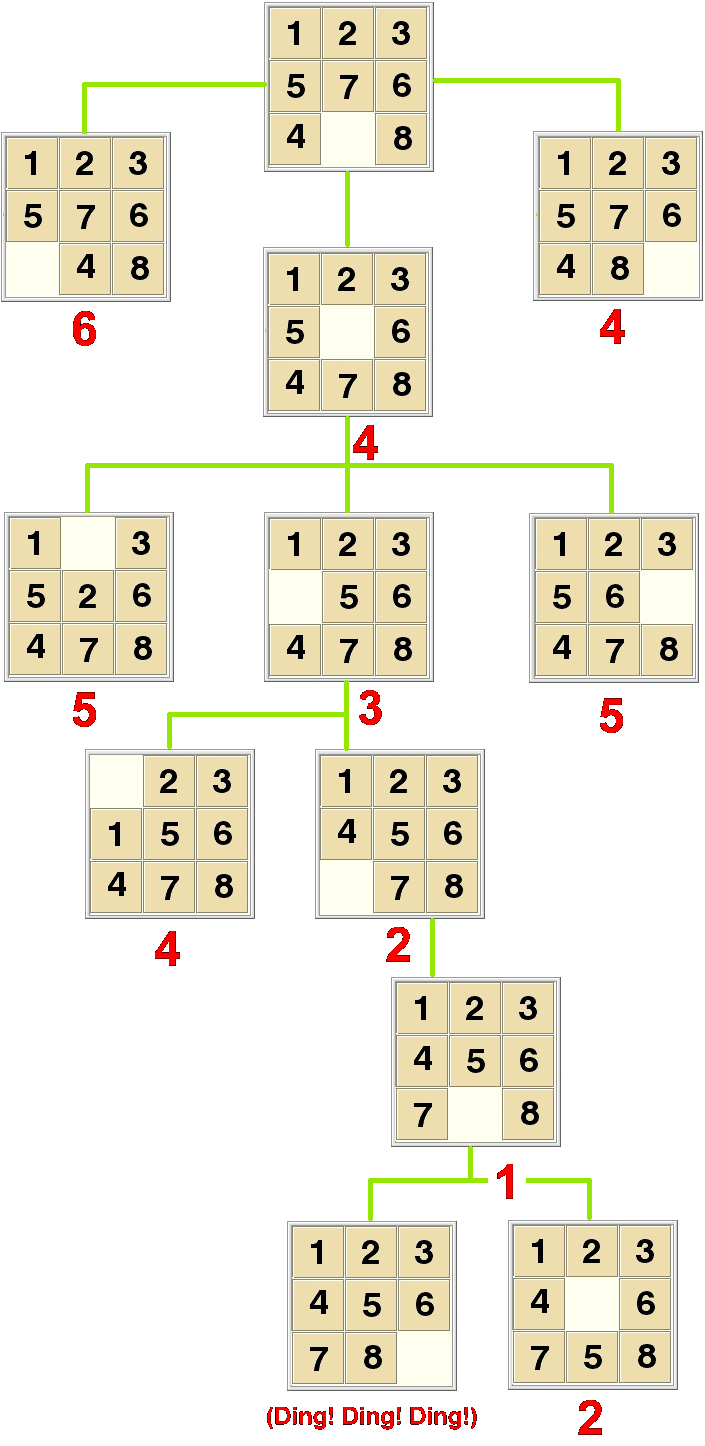
With each state, we compute all states available from it, then choose, from the set of all states ever computed, the one with the lowest "heuristic value." The heuristic value of a given state is a rough measure of how far away it is from the solution.

For this problem, we use the heuristic outlined in section 10.3: the heuristic of a puzzle state is the total, over all the out-of-place tiles, of their distances from their rightful places. For instance, in the starting state, tiles 5, 7, 4 and 8 are out of place. Their distances:

  • Tile 5: 1 move away from its proper place
  • Tile 7: 1 move away from its proper place
  • Tile 4: 1 move away from its proper place
  • Tile 6: 2 move away from its proper place
total heuristic value = 5

Anyway: an example search is illustrated below. We start with the initial state, from which we can reach 3 nearby states of heuristic value 6, 4, and 4. Choosing one of the states with value 4, we find that it leads to three new states of heuristic value 5, 3, and 5. The state of value 3 is the lowest we've seen so far; we stick with that one, which produces two new states of values 4 and 2, and the state of value 2 leads us to a state of value 1, then to the solution. Here's the picture:

Problems 3 and 4

These essay questions have no unique right answer. We wanted you to articulate your thoughts about the issues.