
| COS 126 Recursive Graphics |
Programming Assignment |
Write a program that plots a Sierpinski triangle, as illustrated below. Then, develop a program that plots a recursive pattern of your own design.

Part 1. The Sierpinski triangle is another example of a fractal pattern like the H-tree pattern from Section 2.3 of the textbook. The Polish mathematician Wacław Sierpiński described the pattern in 1915, but it has appeared in Italian art since the 13th century. Though the Sierpinski triangle looks complex, it can be generated with a short recursive program. Your task is to write a program Sierpinski.java with a recursive function sierpinski() and a main() function that calls the recursive function once, and plots the result using standard drawing. Think recursively: sierpinski() should draw one filled equilateral triangle (pointed downwards) and then call itself recursively three (3) times (with an appropriate stopping condition). When writing your program, exercise modular design: include a (non-recursive) function filledTriangle() that draws a filled equilateral triangle of a specified size at a specified location.
Your program shall take one integer command-line argument N, to control the depth of the recursion. All of the drawing should fit snugly inside the equilateral triangle with endpoints (0, 0), (1, 0), and (1/2, √3/2). Do NOT change the scale of the drawing window. First, make sure that your program draws a single filled equilateral triangle when N equals 1. Then, check that it draws four filled equilateral triangles when N equals 2. Your program will be nearly (or completely) debugged when you get to this point.
API specification. Your program Sierpinski.java must be organized as a library of static methods with the following API:
public class Sierpinski
--------------------------------------------------------------------------------
void filledTriangle(double x, double y, double size) // draw shaded equilateral triangle with
bottom vertex (x, y), side length size
void sierpinski(int n, double x, double y, double size) // draw one triangle, bottom vertex (x, y), side size;
recursively call itself three times to generate
the next order Sierpinski triangles above, left
and right of current triangle. n is the order
void main(String[] args) // read order of recursion N as a command-line
argument; draw gray outline triangle with endpoints
(0, 0), (1, 0), and (1/2, 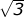 /2); generate an
order-N Sierpinski triangle inside the outline
/2); generate an
order-N Sierpinski triangle inside the outline
Examples. Below are the target Sierpinski triangles for different values of N.
% java-introcs Sierpinski 1 % java-introcs Sierpinski 2 % java-introcs Sierpinski 3 


% java-introcs Sierpinski 4 % java-introcs Sierpinski 5 % java-introcs Sierpinski 6 


A diversion: fractal dimension. In grade school, we learn that the dimension of a line segment is one, the dimension of a square is two, and the dimension of a cube is three. But you probably didn't learn what is really meant by dimension. How can we express what it means mathematically or computationally? Formally, we can define the Hausdorff dimension or similarity dimension of a self-similar figure by partitioning the figure into a number of self-similar pieces of smaller size. We define the dimension to be the log (# self similar pieces) / log (scaling factor in each spatial direction). For example, we can decompose the unit square into 4 smaller squares, each of side length 1/2; or we can decompose it into 25 squares, each of side length 1/5. Here, the number of self-similar pieces is 4 (or 25) and the scaling factor is 2 (or 5). Thus, the dimension of a square is 2 since log (4) / log(2) = log (25) / log (5) = 2. We can decompose the unit cube into 8 cubes, each of side length 1/2; or we can decompose it into 125 cubes, each of side length 1/5. Therefore, the dimension of a cube is log(8) / log (2) = log(125) / log(5) = 3.
We can also apply this definition directly to the (set of white points in) Sierpinski triangle. We can decompose the unit Sierpinski triangle into 3 Sierpinski triangles, each of side length 1/2. Thus, the dimension of a Sierpinski triangle is log (3) / log (2) ≈ 1.585. Its dimension is fractional—more than a line segment, but less than a square! With Euclidean geometry, the dimension is always an integer; with fractal geometry, it can be something in between. Fractals are similar to many physical objects; for example, the coastline of Britain resembles a fractal, and its fractal dimension has been measured to be approximately 1.25.
Part 2. In this part you will create a program Art.java that produces a recursive drawing of your own design. It must take one integer command-line argument N that controls the depth of recursion. It should stay within the drawing window when N is between 1 and 7. It can be a geometric pattern, a random construction, or anything else that takes advantage of recursive functions. For full marks, it should not be something that could be easily rewritten to use loops in place of recursion, and some aspects of the recursive call tree (or how parameters or overlapping are used) should be distinct from the in-class examples (HTree, Sierpinski, NestedCircles, Brownian).
Submission. Submit Sierpinski.java and Art.java. Do not add sound to either file. If your Art.java requires any supplementary image files, submit them as well. Finally, submit a readme.txt file and answer the questions therein.