COS 226 Pattern Recognition Assignment

COS 226 Programming Assignment

Pattern Recognition

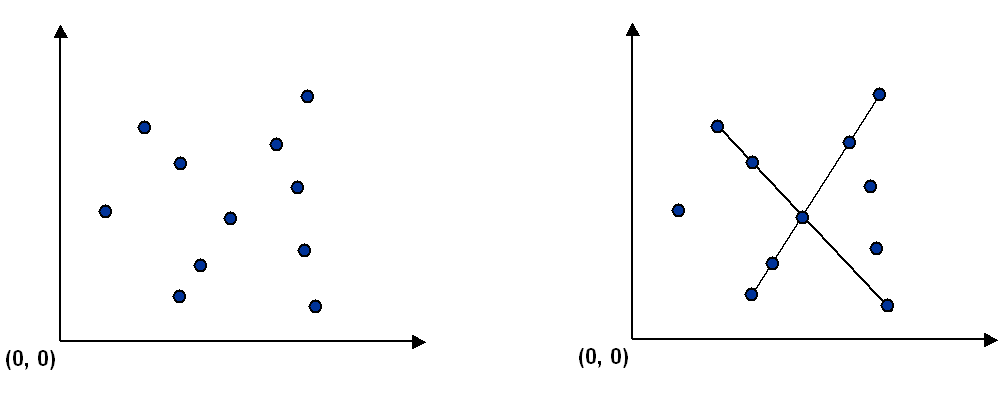
Write a program to recognize line patterns in a given set of points.

Computer vision involves analyzing patterns in visual images and reconstructing the real world objects that produced them. The process in often broken up into two phases: feature detection and pattern recognition. Feature detection involves selecting important features of the image; pattern recognition involves discovering patterns in the features. We will investigate a particularly clean pattern recognition problem involving points and line segments. This kind of pattern recognition arises in many other applications, for example statistical data analysis.

The problem. Given a set of N points in the plane, draw every line segment that connects 4 or more distinct points in the set.

Brute force. Write a program Brute.java that examines 4 points at a time and checks if they all lie on the same line segment, printing out any such line segments to standard output and plotting them using StdDraw. To get started, you may use the data type Point.java and the client program PointPlotter.java which reads in a list of points from standard input and plots them. You will need to supply additional methods in Point.java in order to support the brute force client, e.g., checking whether three or four points lie on the same line.

A sorting solution. Remarkably, it is possible to solve the problem much faster than the brute force solution described above. Given a point p, the following method determines whether p participates in a set of 4 or more collinear points.

Think of p as the origin.
For each other point q, determine the angle it makes with p.
Sort the points according to the angle each makes with p.
Check if any 3 (or more) adjacent points in the sorted order have equal angles with p. If so, these points, together with p, are collinear.

Applying this method for each of the N points in turn yields an efficient algorithm to the problem. The algorithm solves the problem because points that make the same angle with p are collinear, and sorting brings such points together. The algorithm is fast because the bottleneck operation is sorting.

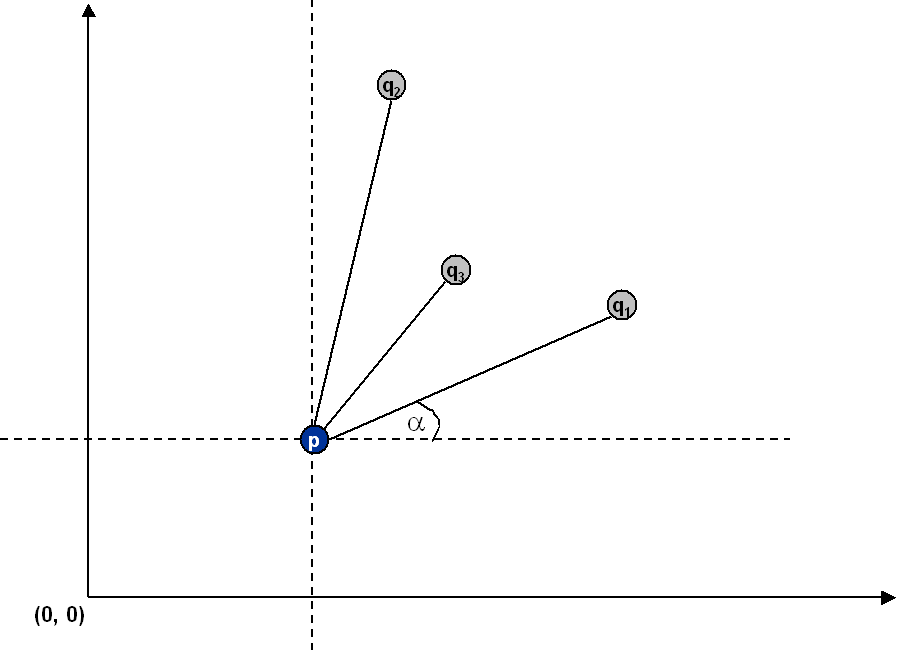
Write a program Fast.java that implements this algorithm using Arrays.sort() and a user-defined Comparator for Point objects.

Input format. The data file consists of an integer N, followed by N pairs of integers (x, y) between 0 and 32,767.

% more input6.txt       % more input8.txt
6                       8
19000  10000             10000      0
18000  10000                 0  10000
32000  10000              3000   7000
21000  10000              7000   3000
 1234   5678             20000  21000
14000  10000              3000   4000
                         14000  15000
                          6000   7000

Output format. Print to standard output the line segments that your program discovers in the format below (number of collinear points in the line segment, followed by the points).

% java Brute < input8.txt
4: (10000, 0) -> (7000, 3000) -> (3000, 7000) -> (0, 10000) 
4: (3000, 4000) -> (6000, 7000) -> (14000, 15000) -> (20000, 21000) 

% java Fast < input6.txt
5: (14000, 10000) -> (18000, 10000) -> (19000, 10000) -> (21000, 10000) -> (32000, 10000)

Also, plot the points and the line segments using standard draw. Using the Point data type supplied, p.draw() draws the point p and p.drawTo(q) draws the line segment from p to q. Before drawing, scale the coordinate system so that coordinates between 0 and 32,767 fit in the graphics window.

For full credit, Fast.java must print and plot a minimal representation: that is, only print one representation of each line segment and don't print subsegments. It's ok if Brute.java does not produce a minimal representation.

Analysis. Estimate (using tilde notation) the running time (in seconds) of your two programs as a function of the number of points N. Provide empirical and mathematical evidence to justify your hypotheses.

Deliverables. Submit the files: Brute.java, Fast.java, Point.java. Also submit any other auxiliary files, if any, that your program needs (excluding our standard libraries). Finally, submit a readme.txt file and answer the questions.