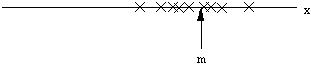
There are two important statistics that we can use to characterize this
collection of examples -- the mean m and the variance v *.
The mean is the arithmetic average or the center of mass:
In general, if the data fall in one cluster, we expect the mean to be
more or less in the center of that cluster. That is, the mean represents
a typical value. The variance is a measure of the size
of the cluster -- how much departure there is from the typical value. It
is defined as the arithmetic average of the square of the deviations from
the mean. To be more precise, the conventional definition is
Clearly, m has the same dimensions as x, but v has those dimensions squared.
The square root of the variance is the RMS value or standard deviation,
s, and it has the same dimensions as x:
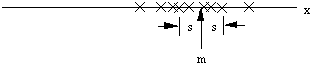
Where the mean measures the location of the center of the cluster, the
standard deviation measures its "radius". It can be shown that
if x has a Gaussian distribution, 68% of the examples will be within one
standard deviation of the mean, and 95% will be within 2 standard deviations.
![]() On to Scaling
On to Scaling ![]() Up to Mahalanobis
Up to Mahalanobis