The k-Means Procedure

Suppose that we have n example feature vectors x₁, x₂, ..., x_n all from the same class, and we know that they fall into k compact clusters, k < n. Let m_i be the mean of the vectors in Cluster i. If the clusters are well separated, we can use a minimum-distance classifier to separate them. That is, we can say that x is in Cluster i if || x - m_i || is the minimum of all the k distances. This suggests the following procedure for finding the k means:

Make initial guesses for the means m₁, m₂, ..., m_k
Until there are no changes in any mean
- Use the estimated means to classify the examples into clusters
- For i from 1 to k
  - Replace m_i with the mean of all of the examples for Cluster i
- end_for
end_until

Here is an example showing how the means m₁ and m₂ move into the centers of two clusters.

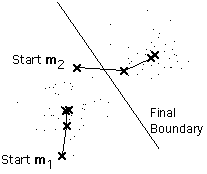
This is a simple version of the k-means procedure. It can be viewed as a greedy algorithm for partitioning the n examples into k clusters so as to minimize the sum of the squared distances to the cluster centers. It does have some weaknesses.

The way to initialize the means was not specified. One popular way to start is to randomly choose k of the examples.
The results produced depend on the initial values for the means, and it frequently happens that suboptimal partitions are found. The standard solution is to try a number of different starting points.
It can happen that the set of examples closest to m_i is empty, so that m_i cannot be updated. This is an annoyance that must be handled in an implementation, but that we shall ignore.
The results depend on the metric used to measure || x - m_i ||. A popular solution is to normalize each variable by its standard deviation, though this is not always desirable.
The results depend on the value of k.

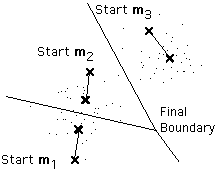
This last problem is particularly troublesome, since we often have no way of knowing how many clusters exist. In the example shown above, the same algorithm applied to the same data produces the following 3-means clustering. Is it better or worse than the 2-means clustering? * The answer can only be found by designing two different classifiers -- one OR-ing together 2 subclasses and the other OR-ing together 3 subclasses -- and seeing which performs better.

__________
* If it turns out to be better, why stop with k = 3 or k = 4 ? If we go to the extreme of k = n, we wind up with what is called a nearest-neighbor classifier. If the number of examples is large enough, a nearest-neighbor classifier can perform excellently. However, it is computationally very expensive. This brings up the point that, like all engineering problems, classifier design is a compromise between price and performance.

On to Fuzzy k-means Up to Clustering