COS 226 Programming Assignment Checklist: Smallest Enclosing Circle

UNDER CONSTRUCTION

Demo

The following applet (written by Xiumin Diao) draws the smallest enclosing circle. Click to add points; drag a point to move it.

Frequently Asked Questions

What should my program do if the input consists of one (or zero) points? In the first case, output a circle centered at the point of radius 0; in the second case report that the input has no points.

What should my program do if a point appears more than once in the input? Handle it correctly.

In the formula for the center and radius of a circle defined by 3 points in the boundary, what happens when the denominator a is zero? Observe that the formula for a is the same as for computing the ccw of three points. When a is zero, the three points are collinear, so they cannot be on the boundary of the same circle (assuming they are distinct).

Are the two or three boundary points that define the circle guaranteed to be on the convex hull? Yes. Feel free to exploit this fact to optimize your solution.

Any hints of faster algorithms? This website describes an Chrystal's algorithm; this website describes another algorithm for the problem.

My answers differ from those in the assignment in the 14th or 15th decimal place. Should I be concerned? No. You are introducing floating point roundoff error into your computation in many places (reading in the decimal points and the arithmetic to compute the center and radius of the circle).

Testing and Submitting

Input.   Here are some sample input files.

Possible Progress Steps

These are purely suggestions for how you might make progress. You do not have to follow these steps.

1. Getting started. Download the directory circle to your system. It contains a number of sample input files.

2. Geometric data types. Implement and thoroughly debug the point and circle data types.

3. Brute force. Don't try to be clever - just implement the algorithm in the simplest way possible.

4. Faster algorithm.

Enrichment

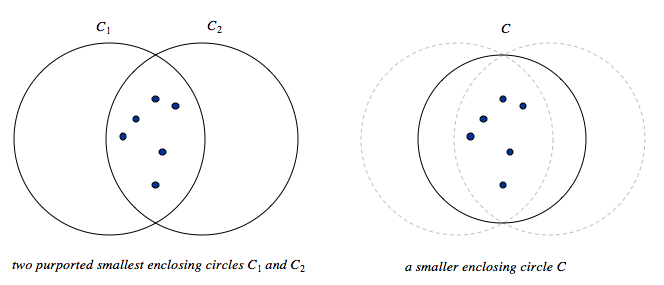
Theorem. Given N points in the plane, the smallest enclosing circle is unique.

Proof. Consider two smallest enclosing circles C₁ and C₂ of radius r and centers c₁ and c₂. Consider the circle C centered at 1/2 (c₁ + c₂) and radius sqrt(r² − a²), where a is one-half the distance between c₁ and c₂. C encloses all of the points since it contains C₁ ∩ C₂.

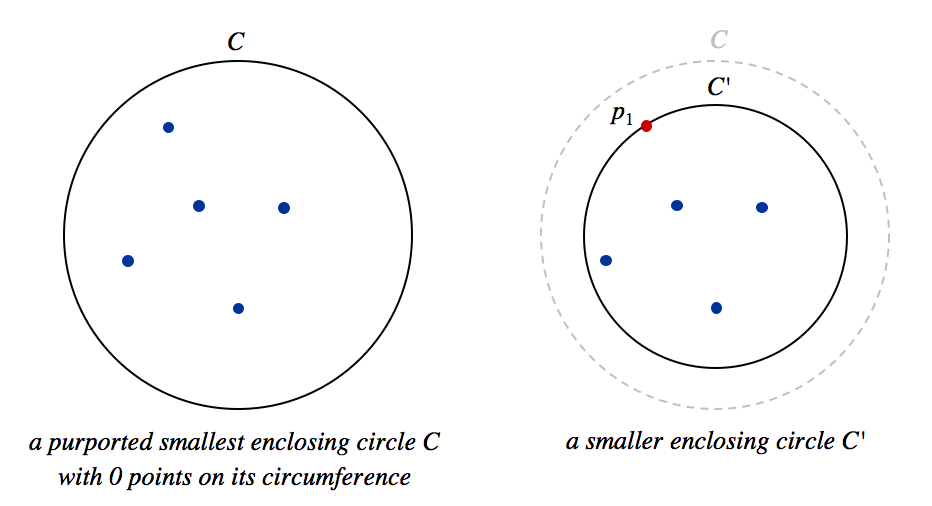
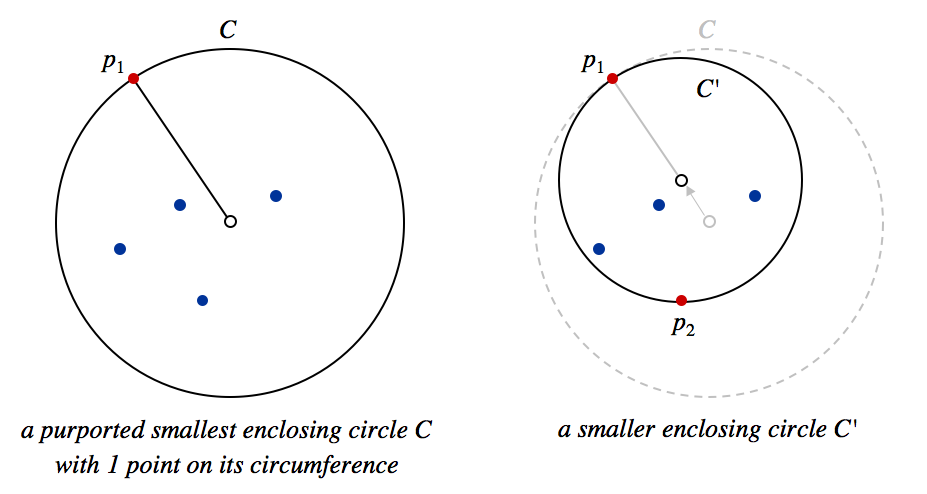
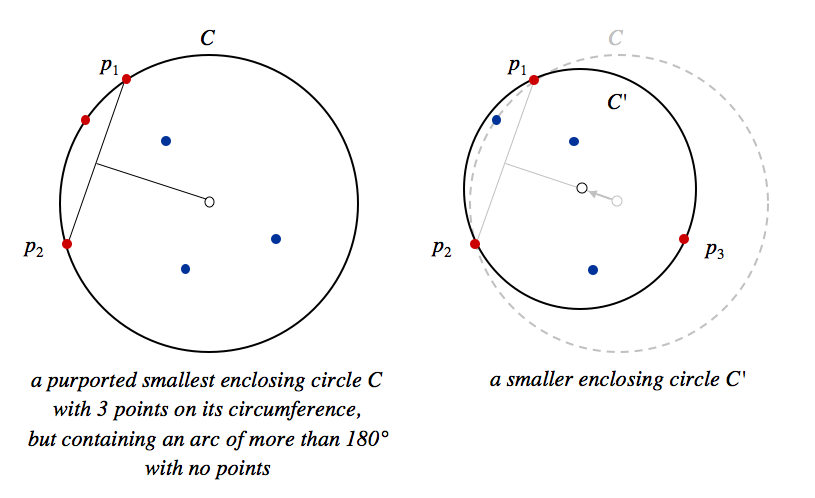
Theorem. Given N ≥ 2 points in the plane, the smallest circle that encloses them contains at least two of the points on its circumference. Moreover, every arc on the circumference of 180 degrees or more contains at least 1 point. (Thus, if the circumference contains exactly two of the points, they are antipodal - exactly 180 degrees apart.)

Proof. The idea is simple: we show that if an enclosing circle C does not have this property, then we can find a smaller circle C' that still encloses all of the points.

• Suppose that C has no points on its circumference. Then, we can decrease the radius of C until it contains at least one point p₁ on its circumference, while still enclosing all of the points.

• Suppose that C has only one point p₁ on its circumference. Then we can move the center of the circle toward p₁ until the circle contains at least one more point p₂ on its circumference.

• Now suppose that C has two (or more) points on its circumference, but it contains an arc of more than 180 degrees with no points. Let p₁ and p₂ be the endpoints of the arc. Keeping p₁ and p₂ on the circumference of the circle, decrease the radius of the circle by moving the center of the circle along the perpendicular bisector of p₁ and p₂. Repeat this until either (i) p₁ and p₂ are antipodal or (ii) the circle contains at least one more point p₃ on its circumference.

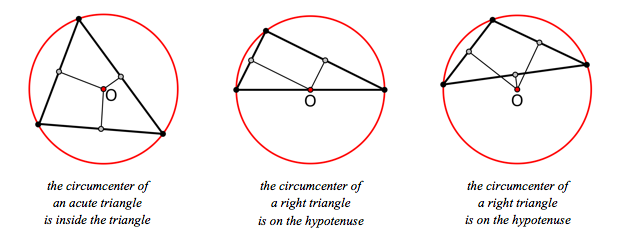
Theorem. A triangle is acute (all angles smaller than 90 degrees) iff its circumcenter (center of the unique circle with the 3 endpoints of the triangle on its circumference) lies inside the triangle; it is obtuse obtuse (has an angle bigger than 90 degrees) iff the circumcenter lies outside the triangle; and it is a right triangle iff the circumcenter lies on one of its sides (a hypotenuse).