Implement the Burrows-Wheeler data compression algorithm. This revolutionary algorithm outcompresses gzip and PKZIP, is relatively easy to implement, and is not protected by any patents. It forms the basis of the Unix compression utililty bzip2.
The Burrows-Wheeler compression algorithm consists of three different algorithmic components, which are applied in succession:
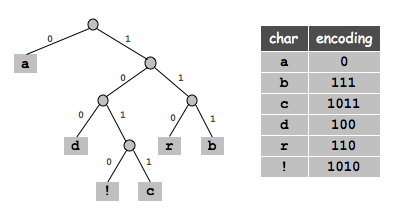
Huffman encoding and encoding. Implement the classic algorithm for arbitrary data. You can base your code on the encoding and decoding algorithms described in class. For example, the Huffman tree corresponding to the input abracadabra! is shown below.

|
Your main task is to pack the bits 8 to the byte when encoding (and unpack them when decoding). Also, your program should handle any input sequence of bytes, whereas the implementation in lecture assumed the input did not contain the '*' character. To do so, represent the Huffman tree by its preorder traversal, but precede each node by the character '0' if it is an internal node, and by the character '1' if it is an external node. On the next line, write the the number of characters you encoded. Finally, on the next line, write the bits, packed 8 to the byte.*a**d*!c*rb // preorder traversal of trie 12 // number of characters to decode 0111110010110100011111001010 // the 28 bits
0*1a0*0*1d0*1!1c0*1r1b // preorder traversal of trie
12 // number of characters to decode
|´| // the 4 bytes of data
Move-to-front encoding. The main idea of move-to-front encoding is to maintain an ordered list of legal symbols, and repeatedly read in symbols from the input message, print out the position in which that symbol appears, and move that symbol to the front of the list. As a simple example, if the initial ordering over a 6 symbol alphabet is a b c d e f, and we want to encode the input caaabcccaccf, then we would update the move-to-front lists as follows
If the same letters occurs next to each other many times in the input, then many of the output values will be small integers, such as 0, 1, and 2. The extremely high frequency of certain symbols makes an ideal scenario for Huffman coding.move-to-front in out ------------- --- --- a b c d e f c 2 c a b d e f a 1 a c b d e f a 0 a c b d e f a 0 a c b d e f b 2 b a c d e f c 2 c b a d e f c 0 c b a d e f c 0 c b a d e f a 2 a c b d e f c 1 c a b d e f f 5 f c a b d e
Your task is to maintain an ordered list of the 256 extended ASCII symbols. Initialize the list by making the ith symbol equal to the ith extended ASCII symbol. Now, read in each character ch from standard input one at a time, output the index in the array where ch appears, and move ch to the front of the list. As an example, the move-to-front encoding of
is given by the following sequence of integers:a b b b a a b b b b a c c a b b a a a b c
Note that 'a' is 97 in ASCII and that we have printed out the indices as type int with separating whitespace using System.out.print() (for debugging only) rather than as type char without separating whitespace using System.out.write() (for the version to submit). Name your program MTFE.java.97 98 0 0 1 0 1 0 0 0 1 99 0 1 2 0 1 0 0 1 2
Move-to-front decoding. Initialize an ordered list of 256 characters, where extended ASCII character i appears ith in the list. Read in each character i (but treat it as an integer between 0 and 255) from standard input one at a time, print the ith character in the list, and move that character to the front of the list. Name your program MTFD.java and check that it recovers any message encoded with MTFE.java.
Burrows-Wheeler transform. The goal of the Burrows-Wheeler transform is not to compress a message, but rather to transform it into a form that is more amenable to compression. The transform rearranges the characters in the input so that that there are lots of clusters with repeated characters, but in such a way that it is still possible to recover the original input. It relies on the following intuition: if you see the letters hen in English text, then most of the time the letter preceding it is t or w. If you could somehow group all such preceding letters together (mostly t's and some w's), then you would have an easy opportunity for data compression.
First treat the input string as a cyclic string and sort the N suffixes of length N. Here is how it works for the text message "abracadabra". The 11 original suffixes are abracadabra, bracadabraa, ..., aabracadabra, and appear in rows 0 through 10 of the table below. Sorting these 11 strings yields the sorted suffixes. Ignore the next array for now - you will only need it for decoding.
The Burrows Wheeler transform t[] is the last column in the suffix sorted list, preceded by the row number where the original string abracadabra ends up.i Original Suffixes Sorted Suffixes t next -- --------------------- --------------------- ---- 0 a b r a c a d a b r a a a b r a c a d a b r 2 1 b r a c a d a b r a a a b r a a b r a c a d 5 *2 r a c a d a b r a a b a b r a c a d a b r a 6 3 a c a d a b r a a b r a c a d a b r a a b r 7 4 c a d a b r a a b r a a d a b r a a b r a c 8 5 a d a b r a a b r a c b r a a b r a c a d a 9 6 d a b r a a b r a c a b r a c a d a b r a a 10 7 a b r a a b r a c a d c a d a b r a a b r a 4 8 b r a a b r a c a d a d a b r a a b r a c a 1 9 r a a b r a c a d a b r a a b r a c a d a b 0 10 a a b r a c a d a b r r a c a d a b r a a b 3
Notice how there are 4 consecutive a's and 2 consecutive b's - this makes the file easier to compress. Write a program BWTE.java to read in a string and output the Burrows-Wheeler transform.2 rdarcaaaabb
Inverting the Burrows-Wheeler transform. Now we describe how to undo the Burrows-Wheeler transform and recover the original message. If the jth original suffix (original string, shifted j characters to the left) is the ith row in the sorted order, then next[i] records the row in the sorted order where the (j+1)st original suffix appears. For example, the 0th original suffix abracadabra is row 2 of the sorted order; since next[2] = 6, the next original suffix bracadabraa is row 6 of the sorted order. Knowing the array next[] makes decoding easy, as with the following Java code:
int N = 11;
int[] next = { 2, 5, 6, 7, 8, 9, 10, 4, 1, 0, 3 };
String t = "rdarcaaaabb";
int x = 2;
for (int i = 0; i < N; i++) {
x = next[x];
System.out.write(t.charAt(x));
}
Amazingly, the information contained in the Burrows-Wheeler
transform is enough to reconstruct next[], and
hence the original message! Here's how.
First, we know all of the characters in the original message,
even if they're permuted in the wrong order.
This enables us to reconstruct the first column in the
suffix sorted list by sorting the characters.
Since 'c' only occurs once in the message and the suffixes are
formed using cyclic wrap-around, we can deduce
that next[7] = 4.
Similarly, 'd' only occurs once, so we can
deduce that next[8] = 1.
However, since 'r' appears twice, it may seem ambiguous whether next[9] = 0 and next[10] = 3, or whether next[9] = 3 and next[10] = 0. Here's the key rule that resolves the ambiguity:i Sorted Suffixes t next -- --------------------- ---- 0 a ? ? ? ? ? ? ? ? ? r 1 a ? ? ? ? ? ? ? ? ? d *2 a ? ? ? ? ? ? ? ? ? a 3 a ? ? ? ? ? ? ? ? ? r 4 a ? ? ? ? ? ? ? ? ? c 5 b ? ? ? ? ? ? ? ? ? a 6 b ? ? ? ? ? ? ? ? ? a 7 c ? ? ? ? ? ? ? ? ? a 4 8 d ? ? ? ? ? ? ? ? ? a 1 9 r ? ? ? ? ? ? ? ? ? b 10 r ? ? ? ? ? ? ? ? ? b
If sorted row i and j both start with the same letter and i < j, then next[i] < next[j].This rule implies next[9] = 0 and next[10] = 3. Why is this rule valid? The rows are sorted so row 9 is lexicographically less than row 10. Thus the nine unknown characters in row 9 must be less than the the nine unknown characters in row 10 (since both start with r). We also know that between the two rows that end with r, row 0 is less than row 3. But, the nine unknown characters in row 9 and 10 are precisely the first nine characters in rows 0 and 3. Thus, next[9] = 0 and next[10] = 3 or this would contradict the fact that the suffixes were sorted.
Name your program BWTD.java and check that it recovers any message encoded with BWTE.java.
Analysis. Once you have all 6 programs working, compress some of these text files. Calculate the compression ratio achieved for each file. Also, report the time to compress and decompress each file.
Input and output. The library StdIn is designed to read in strings composed of Unicode characters, and it is unsuitable for reading in binary data. Instead use the library CharStdIn. It has the following interface.
Similarly, use System.out.write(ch) to write out an extended ASCII character ch as a byte instead of System.out.print(ch).public static boolean isEmpty() // is stdin empty? public static char readChar() // read one byte and return it as a char public static String readLine() // read one line of bytes and return as a String public static String readAll() // read the rest of the input and return as a String