| COS 126 Barnes-Hut Galaxy Simulator |
Programming Assignment Due: Monday, 11:59pm |
In Assignment 2, you created a brute force program to simulate the motion of N bodies, mutually affected by gravitational forces. In this brute force solution, the number of force calculations per step is proportional to N2. The brute force algorithm is not practical when N is large. In this assignment, you will implement the Barnes-Hut algorithm to simulate each step in time proportional to N log N and animate the evolution of entire galaxies. The Barnes-Hut algorithm is the algorithm most scientists use for N-Body simulation.
The Barnes-Hut algorithm. The crucial idea in speeding up the brute force algorithm is to group nearby bodies and approximate them as a single body. If the group is sufficiently far away, we can approximate its gravitational effects by using its center of mass. The center of mass of a group of bodies is the average position of a body in that group, weighted by mass. Formally, if two bodies have positions (x1 , y1) and (x2, y2), and masses m1 and m2, then their total mass and center of mass (x, y) are given by:
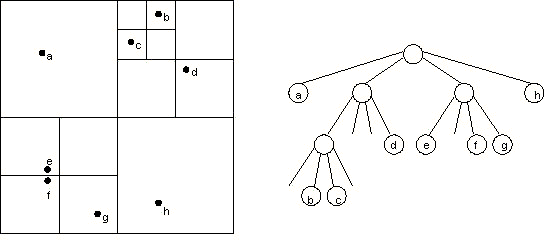
m = m1 + m2The Barnes-Hut algorithm is a clever scheme for grouping together bodies that are sufficiently nearby. It recursively divides the set of bodies into groups by storing them in a quad-tree. A quad-tree is similar to a binary tree, except that each node has 4 children (some of which may be empty). Each node represents a region of the two dimensional space. The topmost node represents the whole space, and its four children represent the four quadrants of the space. As shown in the diagram, the space is recursively subdivided into quadrants until each subdivision contains 0 or 1 bodies (some regions do not have bodies in all of their quadrants. Hence, some internal nodes have less than 4 non-empty children). Each external node represents a single body. Each internal node represents the group of bodies beneath it, and stores the center-of-mass and the total mass of all its children bodies. Here is an example with 8 bodies.
x = (x1m1 + x2m2) / m
y = (y1m1 + y2m2) / m

To calculate the net force on a particular body, traverse the nodes of the tree, starting from the root. If the center-of-mass of an internal node is sufficiently far from the body, approximate the bodies contained in that part of the tree as a single body, whose position is the group's center of mass and whose mass is the group's total mass. The algorithm is fast because we don't need to individually examine any of the bodies in the group. If the internal node is not sufficiently far from the body, recursively traverse each of its subtrees. To determine if a node is sufficiently far away, compute the quotient s / d, where s is the width of the region represented by the internal node, and d is the distance between the body and the node's center-of-mass. Then, compare this ratio against a threshold value θ. If s / d < θ, then the internal node is sufficiently far away. By adjusting the θ parameter, we can balance the speed and accuracy of the simulation. We will always use θ = 0.5, a value commonly used in practice. Note that if θ = 0, then no internal node is treated as a single body, and the algorithm degenerates to brute force.
Constructing the Barnes-Hut tree. To construct the Barnes-Hut tree, insert the bodies one after another. To insert a body b into the tree rooted at node x, use the following recursive procedure:
As an example, consider the 5 bodies in the diagram below. In our examples, we use the convention that the branches, from left to right, represent the northwest, northeast, southwest, and southeast quadrants, respectively. The tree goes through the following stages as the bodies are inserted:
The root node contains the center-of-mass and total mass of all five bodies. The two other internal nodes each contain the center-of-mass and total mass of the bodies b, c, and d.
Calculating the force acting on a body. To calculate the net force acting on body b, use the following recursive procedure, starting with the root of the quad-tree:
Your Assignment. Implement the Barnes-Hut algorithm and animate the results using Turtle graphics.
public Quad(double xmid, double ymid, double length):
create a new quadrant centered at (xmid, ymid) of the given side length.
public boolean contains(double x, double y):
Return true if (x, y) is in the quadrant, and false otherwise.
public double length(): Returns the length of a side
of the quadrant.
public Quad NW(), NE(), SW(), and SE(): These four methods
create and return a new Quad representing a sub-quadrant of
the invoking quadrant.
public boolean in(Quad q): Returns true if the invoking
body is in quadrant q and false otherwise.
public Body plus(Body b): return a new Body that
represents the center-of-mass of the the invoking body a and b.
Use the formula provided above.
public class BHTree {
private Body body; // body or aggregate body stored in this node
private Quad quad; // square region that the tree represents
private BHTree NW; // tree representing northwest quadrant
private BHTree NE; // tree representing northeast quadrant
private BHTree SW; // tree representing southwest quadrant
private BHTree SE; // tree representing southeast quadrant
}
updateForce to recalculate it.
Then, update the positions of the bodies and plot them.