This test is 15 questions, weighted as specified, for a total of 100 points. Do all of your work on these pages (use the back for scratch space), giving the answer in the space provided. Put your name and login on the test (now), and write out and sign the Honor Code pledge before turning in the test. You have three hours to complete the test.

``I pledge my honor that I have not violated the Honor Code during this examination.''

         1.   ____           6.  ____          11.  ____

         2.   ____           7.  ____          12.  ____

         3.   ____           8.  ____          13.  ____

         4.   ____           9.  ____          14.  ____

         5.   ____          10.  ____          15.  ____



        SUB   ____          SUB  ____          SUB  ____





     TOTAL:   ____

1. (5 points) The following table gives the KMP state transitions for the string 1011011010, except for one state transition, labeled X in the table. What should the value of X be?

                    0   1   2   3   4   5   6   7   8   9  10
                  --------------------------------------------
               0 |  0   2   0   2   5   0   2   8   0  10  10
               1 |  1   1   3   4   1   6   7   1   9   X  10
   

   
   
   
   
   
   
   
   
   

2. (5 points) Draw the binary trie that represents the dictionary that is constructed by the LZW algorithm for the string "aaabaabaaa".

    
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   

3. (5 points) Draw the subdivision of the plane that corresponds to inserting the following points into an initially empty 2D tree, in the order given.

      (1, 1)  (2, 2)  (3, 3)  (4, 4)  (5, 5)  (6, 6)  (7, 7) 
   

   
   

    

   
   
   
   
   
   
   

    

4. (4 points) Which one of the following statements is true regarding the asymptotic running time of computing a 2D tree for a set of N points? Circle your answer.

   1. guaranteed quadratic always

   2. guaranteed N log N always

   3. guaranteed linear always

   4. for any point set, some ordering of the points leads to linear time

   5. for any point set, no ordering of the points leads to better than N log N time

   
   
   

5. (8 points) Consider the graph on five nodes, labeled 0 through 4, with the 7 undirected edges

      0-1 0-2 0-3 1-2 1-3 2-3 3-4
   

   1. How many of the 14 edges (each listed edge and its reverse) does a DFS examine in the worst case to find a path from 0 to 4? The graph is represented using a standard adjacency list, but the edges are inserted in arbitrary order rather than the order listed above.

      
      
      
      
      
      
      
      
      
      
      
      
      
      
      

   2. Answer the same question for BFS. Assume that duplicate nodes are not put onto the BFS queue.

      
      
      
      
      
      

   
   
   
   
   
   
   

6. (5 points) Consider the digraph on five nodes, labeled 0 through 4, with six directed edges

   0-1 1-4 4-0 0-2 2-3 3-2
   

   List the strongly connected components of this digraph.

   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   

7. (5 points) Give the transitive closure of the graph in question 6.

                        TO
   
                0    1    2    3    4  
            -------------------------
           |  
         0 |    1
           |
     F   1 |         1
     R     |              
     O   2 |              1     
     M     |
         3 |                   1
           |
         4 |                        1
   

   
   
   
   
   
   
   
   
   
   
   
   
   
   

8. (6 points) Alan has discovered an amazing new algorithm for the mincost maxflow problem. Alan has done some preliminary computational experiments that appear to indicate the potential utility of the new algorithm, in particular it appears much faster than Beth's classic algorithm.

              running time (seconds)
   
     N         Alan           Beth
   -------------------------------
     5         0.00           0.01  
    10         0.00           0.05
    20         0.01           0.16
    40         0.05           0.63
    80         0.41           2.51
   160         3.27          10.20
   
   

   Estimate the asymptotic running time of the algorithms as a function of N. Predict how long (in days) that each of the two algorithms will take to solve an instance of size N = 16,000 and N = 32,000.

               Asymptotic         Time (days)      Time (days)
   Algorithm   Running Time       N = 16,000       N = 32,000
   -----------------------------------------------------------
   
     Alan        O (      )
   
     Beth        O (      )
   

   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   

9. (8 points) Consider the undirected network below.

   

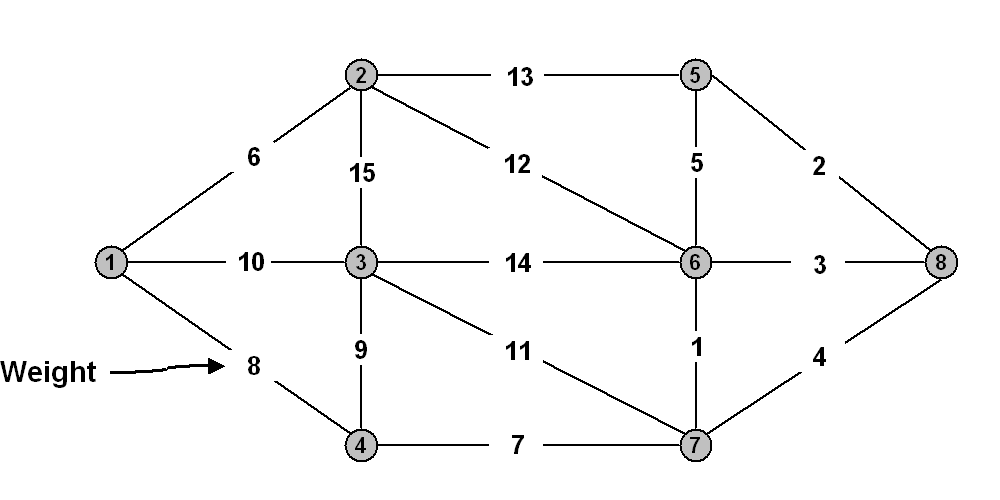
   1. Run Prim's algorithm starting at vertex 1 and list the order in which the vertices are examined.

      
      
      
      
      
      
      
      

   2. Give the cost of the MST.

      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      
      

10. (8 points) Consider the directed network below.

    

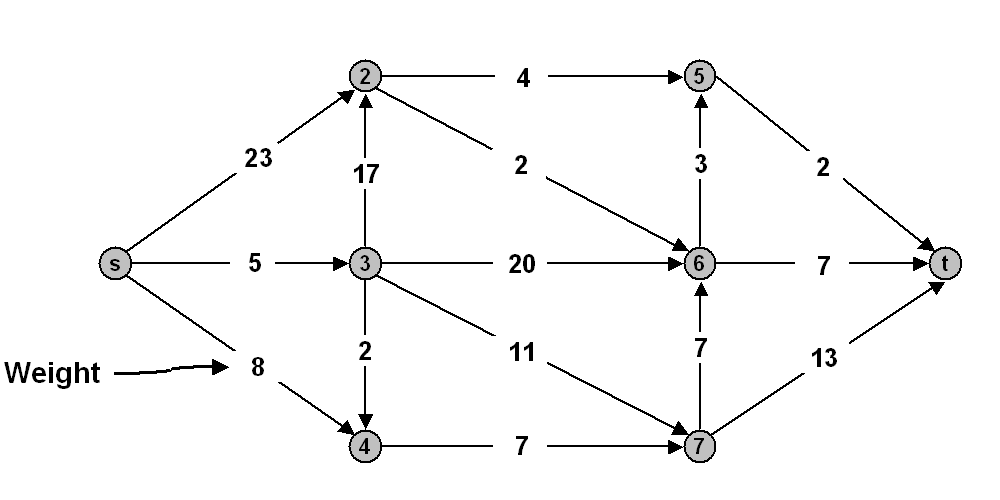
    1. Run Dijkstra's algorithm on the network above and list the order in which the vertices are examined.

       
       
       
       
       
       
       
       
       
       
       
       
       

    2. Give the length of the shortest path from s to t and also write down the path itself.

       
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       

11. (12 points) Consider the boxed flow of value 24 in the maxflow network below.

    

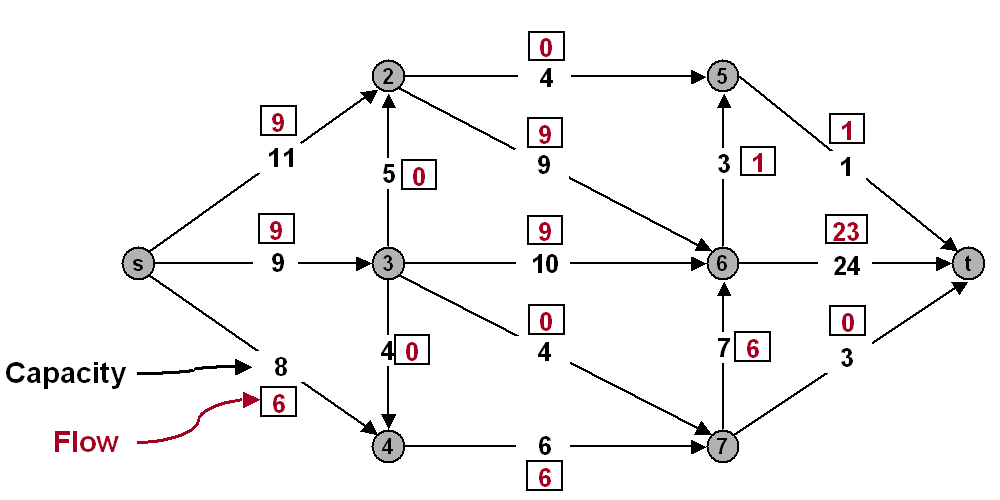
    1. Perform one iteration of the Ford-Fulkerson augmenting path algorithm. Write the augmenting path below and the value of the resulting flow.

       
       
       
       
       
       
       
       
       

    2. List the vertices on the source side of a mincut in the network above. Also, write the value of the mincut.

       
       
       
       
       
       
       
       
       

    3. Suppose that the capacity of the arc 4-7 is decreased from 6 to 5. Without re-solving the resulting maxflow problem, argue concisely (10 words or less), but rigorously, why the maxflow value must decrease.

    
    
    
    
    
    
    

12. (8 points) You are the investment manager for a small company. You can purchase three types of assets, each of which costs $100,000 per unit. Assets can be purchased in whole or fractional units. The assets produce income 5, 10, and 20 years from now, and that income is needed to cover minimum cash flow requirements in those years. Your goal is to minimize the cost of the assets purchased. Note: cash from a previous year cannot be carried over to meet the cash flow requirement for a subsequent year.

    Year   Asset 1   Asset 2    Asset 3    Cash flow required
    ---------------------------------------------------------
     5         200       100         50                  4000
    10          50        50        100                  1000
    20           0       150        200                  3000
    

    1. Formulate the problem as a linear programming problem.

       
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       
       

    2. Transform the problem to standard form, i.e., nonnegative variables, equality constraints, and maximization.

    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    

13. (5 points) Circle each statement about reduction below that is not known to be true.

    1. Assignment reduces to Mincost Maxflow

    2. Longest path reduces to Shortest Path with Nonnegative Weights

    3. Maxflow reduces to Mincut

    4. Mincut reduces to Maxflow

    5. Maxflow reduces to Linear Programming

    
    
    
    
    

14. (9 points) Match up each algorithm with a data structure that is critical for implementing it.

    
    _____ BFS                    A.  2D tree
    
    _____ DFS                    B.  Adjacency matrix
    
    _____ Floyd / Warshall       C.  Binary trie
    
    _____ Kruskal                D.  Deque
    
    _____ LZW                    E.  Parent-link
    
    _____ NFSA simulator         F.  Priority queue
    
    _____ Network simplex        G.  Queue
    
    _____ PFS                    H.  Stack
    
    _____ Range searching        I.  Union-find
    

    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    
    

15. (8 points) This question is in regard to your part-time job working for a software technology company. Your boss (having been told by you on the basis on your 126 knowledge that the company had better not bet its future on developing an application that finds an optimal tour connecting a set of cities) is still looking for a challenging project for you. Your boss is willing to invest in things that might be difficult, but not things that we know to be impossible or that we believe to be intractable. On the basis of your 226 knowledge, which of the following ideas can you tell your boss to forget about? Circle all that apply.

    1. An FSA-based search engine interface that allows users to specify a richer set of patterns than does "grep"

    2. A linear-time maxflow algorithm

    3. An algorithm that compresses any given file by ten percent

    4. A linear-time algorithm for finding the MST of a set of points in the plane that can only compare the distances between two points (not know their coordinate values)

    5. A linear-time algorithm for finding the MST of a graph with positive edge weights

    6. A linear-time algorithm for sorting a set of numbers that can only compare two numbers (not know their values)

    7. An algorithm that finds the longest path connecting two vertices in a network with positive edge weights

    8. An algorithm that finds the shortest path connecting two vertices in a network with positive edge weights