|
|
What preparation do I need before beginning this assignment? Read Sections 2.1–2.3 of the textbook.
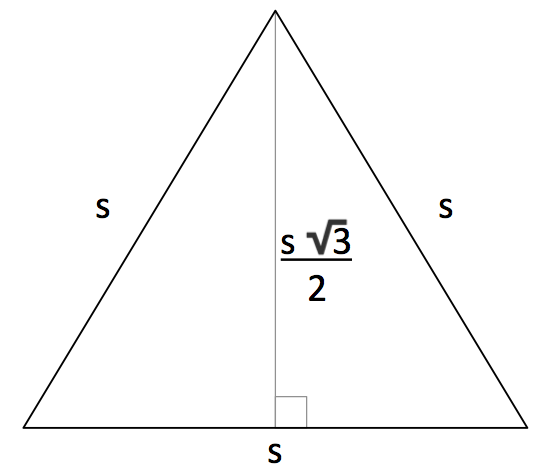
What is the formula for the height of an equilateral triangle of side length s? The height is \(s \sqrt{3} / 2 \).

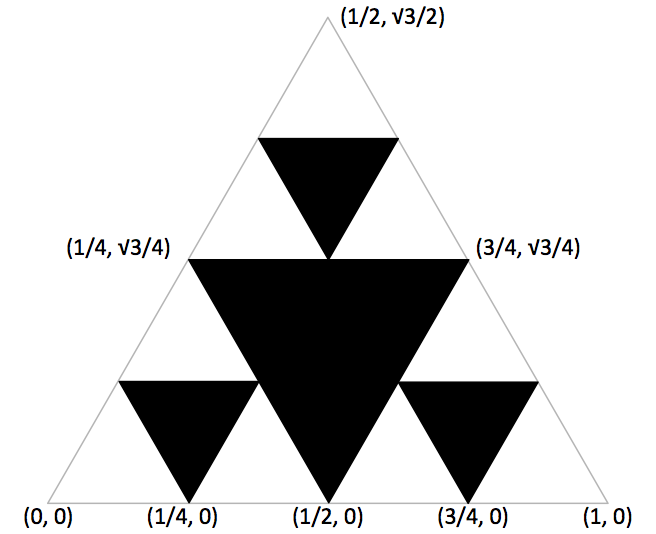
What is the layout of the initial equilateral triangle? The top vertex lies at \((1/2, \sqrt{3} / 2)\) We illustrate the coordinates of the initial iterations below to help you double-check.
How do I draw a filled equilateral triangle?
Call the method StdDraw.filledPolygon() with appropriate arguments.
I get a StackOverflowError message even when N is a very small number like 3. What could be wrong? This means you are running out of space to store the function-call stack. Often, this error is caused by an infinite recursive function. Be sure you have correctly defined your base case and your reduction step.
|
|
The API checker says that I need to make my methods private. How do I do that? Use the access modifier private instead of public in the method signature. A public method can be called directly by a method in another class; a private method cannot. The only public method that you should have in Art is main().
How should I approach the artistic part of the assignment? This part is meant to be fun, but here are some guidelines in case you're not so artistic. A very good approach is to first choose a self-referential pattern as a target output. Check out the graphics exercises in Section 2.3. Here are some of our favorite student submissions from last semester. See also the Famous Fractals in Fractals Unleashed for some ideas. Here is a list of fractals, by Hausdorff dimension. Some pictures are harder to generate than others (and some require trigonometry); consult your preceptor for advice if you're unsure.
What will cause me to lose points on the artistic part? We consider three things: the structure of the code; the structure of the recursive function-call tree; and the art itself.
For example, the Quadricross looks very different from the in-class examples, but the code to generate it looks extremely similar to HTree, so it is a bad choice. On the other hand, even though the Sierpinski Curve eventually generates something that looks identical to the Sierpinski Triangle, the code is very different (probably including an "angle" argument in the recursive method) and so it would earn full marks.
Possible ideas include:
You will also lose points if your artwork can be created just as easily without recursion (like Factorial for example). If the recursive function-call tree for your method is a straight line, it probably falls under this category.
May I use .gif, .jpg, or .png in my artistic creation? Yes. If so, be sure to submit them along with your other files. Make it clear in your readme.txt what part of the design is yours and what part is borrowed from the image file.
My function for Art.java takes several parameters, but the assignment says that I can only read in one command-line argument N. What should I do? Choose a few of the best parameter values and do something like the following:
if (N == 1) { x = 0.55; y = 0.75; n = 3; }
else if (N == 2) { x = 0.55; y = 0.75; n = 5; }
else if (N == 3) { x = 0.32; y = 0.71; n = 8; }
else if ...
How can I create colors that aren't predefined in standard drawing? It requires using objects that we'll learn about in Chapter 3. In the meantime, you can use this color guide.
|
|
These are purely suggestions for how you might make progress. You do not have to follow these steps. Note that your final Sierpinski.java program should not be very long (no longer than Htree, not including comments and blank lines).
Test your height() function.
To debug and test your function, write main() so that it calls filledTriangle() a few times, with different parameters. You will be able to use this function without modification in Sierpinski.java.
|
|
|
|
After you have completed the assignment, consider using our StdDraw3D library instead of StdDraw to create a three-dimensional fractal design! (Note: You will receive no credit for submitting an Art.java that uses StdDraw3D. Sorry.)
If you used our autoinstaller, StdDraw3D should be available. To check, type the following at the Terminal / Command Prompt:
java-introcs StdDraw3D
|
|