| COS 126 Hamming Codes in TOY |
Programming Assignment |
Write a TOY program to encode data using Hamming codes. Then write a TOY program to correct encoded data that has been corrupted.
Perspective. Error-correcting codes enable data to be sent through a noisy communication channel without corruption. To accomplish this, the sender appends redundant information to the message, so that even if some of the original data is corrupted during transmission, the receiver can still recover the original message intact. Transmission errors are common and can arise from scratches on a CD, static on a cell phone, or atmospheric interference. In a noisy environment, error-correcting codes can increase the throughput of a communication link since there is no need to retransmit the message if it becomes partially corrupted during transmission. For this reason, error-correcting codes are used in many common systems, such as storage devices (CD, DVD, DRAM), mobile communication (cell phones, wireless, microwave links), and digital television.
Hamming Codes. A Hamming code is a specific type of error-correcting code that allows the detection and correction of single-bit transmission errors. Hamming codes are used in many applications where such errors are common, including DRAM memory chips and satellite communication hardware. Hamming codes work by repeatedly reading four message bits, which we denote by m1, m2, m3, m4, and then inserting three parity bits, which we denote by p1, p2, and p3. If any one of these seven bits is corrupted during transmission, the receiver can detect the error and recover the original four message bits intact. This is called single-bit error correction because at most one bit can be corrected per unit of data sent. The overhead for using this method is a 75% increase in bandwidth because it requires three extra parity bits for every four message bits. An alternative approach of sending three copies of each bit (and using the one that appears most frequently) results in a 200% increase in bandwidth.
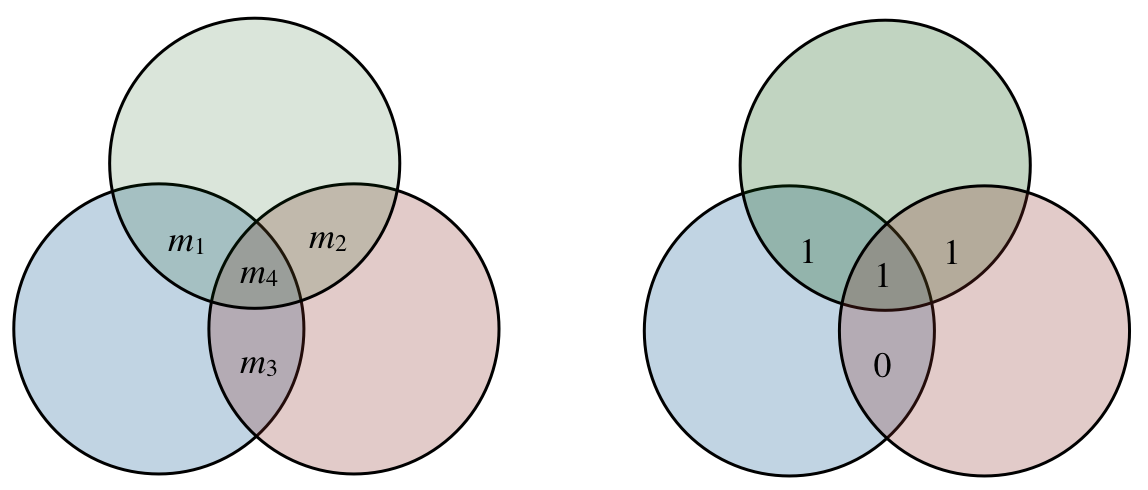
Before we describe the algebra of Hamming codes, we first visualize the calculation of the parity bits using Venn diagrams. As an example, suppose we wish to send the 4-bit message 1101. We associate each of the four message bits with a specific intersection region of three pairwise overlapping circles, as illustrated below:



Now, imagine this picture is transmitted over a noisy communication channel, and that one bit is corrupted so that the following picture arrives at the receiving station (corresponding to 1001100):

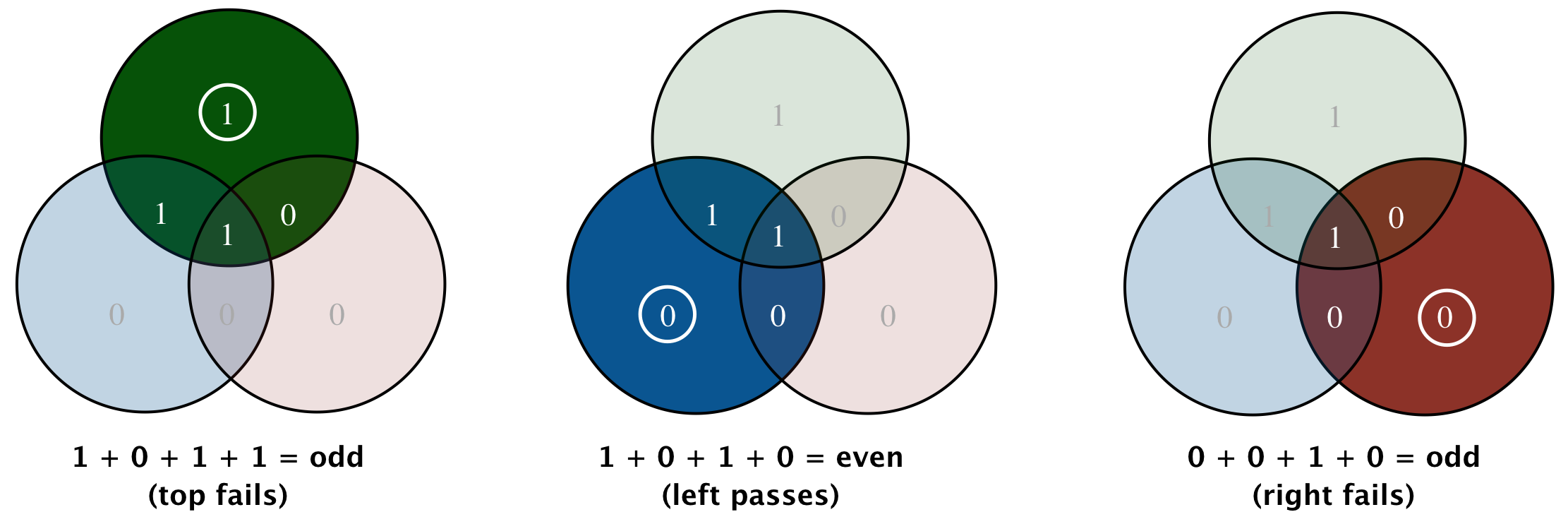
If the center bit m4 is corrupted, then all three parity checks will fail. If a parity bit itself is corrupted, then only one parity check will fail. If the communication channel is so noisy that two or more bits are simultaneously corrupted, then the scheme will not work. Can you see why? More sophisticated types of error-correcting codes can handle such situations.
Of course, in practice, only the seven bits are transmitted, rather than the Venn diagrams.
Part 1. Write a TOY program encode.toy to encode a binary message using the scheme described above. Repeatedly read 4 bits m1, m2, m3, and m4 from TOY standard input and write the 7 bits m1, m2, m3, m4, p1, p2, p3 to TOY standard output. Stop upon reading FFFF from standard input.
Recall that ^ is the exclusive or operator in Java and TOY. This captures the parity notion described above.Part 2. Write a TOY program decode.toy to correct a Hamming encoded message. Repeatedly read 7 bits m1, m2, m3, m4, p1, p2, p3 from TOY standard input and write 4 bits to TOY standard output. Stop upon reading FFFF from standard input. Recall, to determine which one, if any, of the message bits is corrupted, perform the parity checks:
Input format. The input format for encode.toy is a text file that contains the sequence of bits to be transmitted. Each line consists of a sequence of 4 bits, with each bit specified as a 4-digit hexadecimal integer (either 0000 or 0001), separated by whitespace. The last line consists of the single integer FFFF. The input format for decode.toy is the same, except that each line consists of a sequence of 7 bits. Here are input files for encode.toy and decode.toy in the specified format:
Files for this assignment. The file hamming.zip includes two Java programs that illustrate the encoding and decoding procedures; sample input and output files for both encode.toy and decode.toy; the TOY reference card; the readme.txt template; a sample TOY program; and the TOY simulator TOY.java.
Using the TOY simulator. To execute your TOY program using the command-line simulator TOY.java, type the commands that appear in bold below. You should see the following output:
Alternatively, you can use the Visual X-TOY simulator.
Documentation. Include a standard header at the top of each TOY program; comment each line of TOY code with the corresponding pseudocode; optionally, include a comment describing the Java equivalent. See multiply.toy for an example. In the readme.txt file, describe what you used each of the registers for in your programs.
Submission. Submit encode.toy, decode.toy, and a completed readme.txt.
Leaderboard (optional). Rewrite decode.toy using the fewest number of (nonzero) words of TOY main memory. Submit decode.toy to the leaderboard for class fame and glory. Under 40 (in decimal) is very good; under 35 is great; the all-time record is 29.