COS441 Lecture 5

Princeton University
Computer Science Dept.

Computer Science 441
Programming Languages
Fall 1998

Lecture 5

Abstraction

Programming language creates a virtual machine for programmer

Dijkstra: Originally we were obligated to write programs so that a computer could execute them. Now we write the programs and the computer has the obligation to understand and execute them.

Progress in programming language design marked by increasing support for abstraction.

Computer at lowest level is set of charged particles racing through wires w/ memory locations set to one and off - very hard to deal with.

In computer organization look at higher level of abstraction: interpret sequences of on/off as data (reals, integers, char's, etc) and as instructions.

Computer looks at current instruction and contents of memory, then does something to another chunk of memory (incl. registers, accumulators, program counter, etc.)

When write Pascal (or other language) program - work with different virtual machine.

Integers, reals, arrays, records, etc. w/ associated operations

Language creates the illusion of more sophisticated virtual machine.

Pure translators

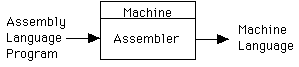
Assembler:

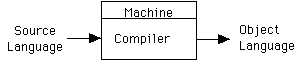
Compiler:

Preprocessor:

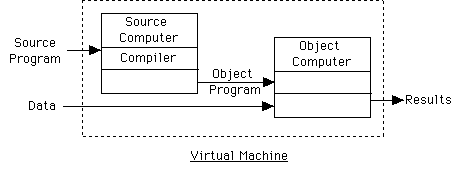
Execution of program w/ compiler:

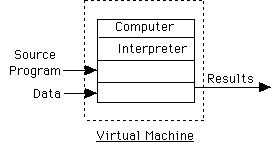
Interpreter:

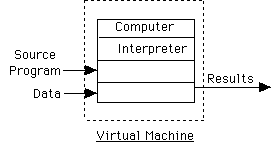
We will speak of virtual machine defined by a language implementation.

Machine language of virtual machine is set of instructions supported by translator for language.

Layers of virtual machines on Mac: Bare 680x0 chip, OpSys virtual machine, MacPascal (or Lightspeed Pascal) machine, application program's virtual machine.

We will describe language in terms of virtual machine

Slight problem:

Different implementors may have different conceptions of virtual machine
Different computers may provide different facilities and operations
Implementors may make different choices as to how to simulate elts of virtual computer

May lead to different implementations of same language - even on same machine.

Problem : How can you ensure different implementations result in same semantics?

Sometimes virtual machines made explicit:

Pascal P-code and P-machine,
Modula-2 M-machine and M-code,
Java virtual machine.

Compilers and Interpreters

While exist few special purpose chips which execute high-level languages (LISP machine) most have to be translated into machine language.

Two extreme solutions:

Pure interpreter: Simulate virtual machine (our approach to run-time semantics)

    REPEAT
        Get next statement
        Determine action(s) to be executed
        Call routine to perform action
    UNTIL done

Pure Compiler:

Translate all units of program into object code (say, in machine language)
Link into single relocatable machine code
Load into memory

Comparison of Compilation vs Interpretation

compiler	interpreter
Only translate each statement once	Translate only if executed
Speed of execution	Error messages tied to source More supportive environment
Only object code in memory when executing. May take more space because of expansion	Must have interp. in memory when executing (but source may be more compact)

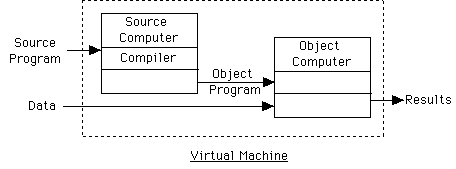
Rarely have pure compiler or interpreter.

Typically compile source into more easy to interpret form.
Ex. Remove white space & comments, build symbol table, or parse each line and store in more compact form (e.g. tree)

Can go farther and compile into intermediate code (e.g., P-code) and then interpret.

In FORTRAN, Format statements (I/O) are always interpreted.

Overview of structure of a compiler

Two primary phases:

Analysis:: Break into lexical items, build parse tree, generate simple intermediate code (type checking)
Synthesis:: Optimization (look at instructions in context), code generation, linking and loading.

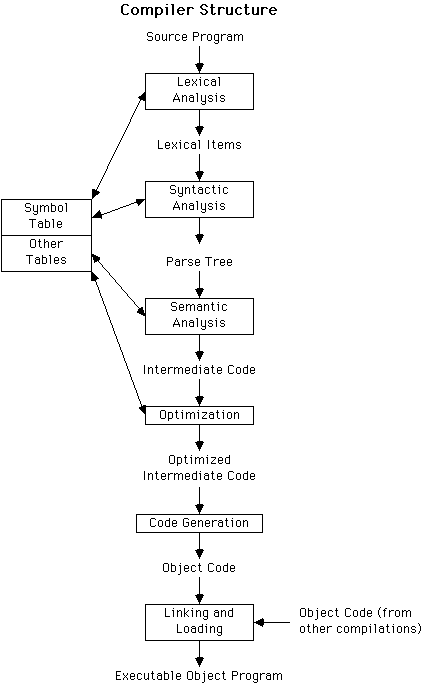
Lexical analysis:

Break source program into lexical items, e.g. identifiers, operation symbols, key words, punctuation, comments, etc. Enter id's into symbol table. Convert lexical items into internal form - often pair of kind of item and actual item (for id, symbol table reference)

Syntactical analysis:

Use formal grammar to parse program and build tree (either explicitly or implicitly through stack)

Semantic analysis:

Update symbol table (e.g., by adding type info). Insert implicit info (e.g., resolve overloaded ops's - like "+"), error detection - type-checking, jumps into loops, etc. Traverse tree generating intermediate code

Optimization:

Catch adjacent store-reload pairs, eval common sub-expressions, move static code out of loops, allocate registers, optimize array accesses, etc.
Example:

   for i := .. do ...
       for j:= 1 to n do
           A[i,j] := ....

Code generation:

Generate real assembly or machine code (now sometimes generate C code)

Linking & loading:

Get object code for all pieces of program (incl separately compiled modules, libraries, etc.). Resolve all external references - get locations relative to beginning location of program. Load program into memory at some start location - do all addressing relative to base address.

Symbol table: Contains all identifier names, kind of id (vble, array name, proc name, formal parameter), type of value, where visible, etc. Used to check for errors and generate code. Often thrown away at end of compilation, but may be held for error reporting or if names generated dynamically.

Like to have easily portable compilers front-end vs back-end

Front-end generate intermediate code and do some peep-hole optimization

Back-end generate real code and do more optimization.

Semantics

Meaning of a program (once know it is syntactically correct).

Operational semantics for most of course.
How would an interpreter for the language work on virtual machine?

Work with virtual (or abstract) machine when discuss semantics of programming language constructs.

Represent Code and Data portions of memory
Has instruction pointer, ip , incremented by one after each command if not explicitly modified by the instruction.

Run program by loading it into memory and initializing ip to beginning of program

Official language definitions: Standardize syntax and semantics - promote portability.

All compilers should accept the same programs (i.e. compile w/o errors)
All legal programs should give the same answers (modulo round-off errors, etc)
Designed for compiler writers and as programmer reference.

Often better to standardize after experience. -- Ada standardized before a real implementation.

Common Lisp, Scheme, ML now standardized, Fortran '9x.

Good formal description of syntax, semantics still hard.

Backus, in Algol 60 Report promised formal semantics.

Said forthcoming in few months - still waiting.
Years after introduction still problems and ambiguities remaining.

Lambda Calculus

Think of the lambda calculus as an assembly language for functional programming languages.

    <exp> ::= <id> | λ<id>.<exp> | <exp> <exp> | (<exp>)
     <id> ::= x | y | ...

λx.E represents a function with formal parameter x, and is equivalent to ML's

   fn x => E

M N represents the application of a function Mto actual parameter N.

The pure lambda calculus does not include numbers, booleans, arithmetic operations, etc., but we will occasionally use them in examples.

   (λx.x+5) 7

evaluates to 12 using the same kind of rule we discussed earlier in the term, which involves substituting the actual parameter in place of the formal parameter. To explain this we must carefully define substitution in terms.

First we give a definition of free variables:

Definition:

FV(x) = {x}
FV(λx.M) = FV(M) - {x}
FV(M N) = FV(M) ∪ FV(N)

We write [N/x] M to denote replacing all (free) occurrences of x by M in term N.

Definition:

[N/x] x = N
[N/x] y = y, if y ≠ x
[N/x] (L M) = ([N/x] L) ([N/x] M)
[N/x](λy.M) = λy. ([N/x] M), if y ≠ x and y not in FV(N).

Once we have this notation, we can consider the reduction or evaluation rules for the lambda calculus:

(α)λx.M →_α λ y. ([y/x] M), if y not occur in M.

(β) (λx.M)N →_β [N/x] M

(η)λx.(M x) →_η M

Other ( δ) rules may be introduced to take care of constants (like arithmetic operations). We write M → N when we don't wish to distinguish between the types of reduction rules.

Now we can see how the earlier example works:

(λx.x+5) 7 →_β 7+5 → _δ 12

We'll talk about the order of applying reduction later, for now we simply note that one can apply a reduction rule to any subterm of a lambda expression. Thus if M is a lambda expression, then M (( λx.x+5) 7) reduces to M 12.

From now on we will concentrate on the pure lambda calculus (no constants).

Definability in the lambda calculus

Even without constants for natural numbers, we can define terms that behave like the natural numbers. In Peano arithmetic, the natural numbers are defined as follows:

0 is a natural number
If n is a natural number, then so is Succ n.

Thus Succ (Succ (Succ 0))) represents the natural number 4.

We'd like to emulate this construction with the lambda calculus. Unfortunately we don't have constants 0 and Succ, so we'll use variable z to stand for 0 and s to stand for Succ. We'll make these formal parameters of our number encodings just in case someone provides us with the real thing:

    0 = λz.λs.z
    1 = λz.λs.s z
    2 = λz.λs.s (s z)
    ...
    n+1 = λz.λs.s (n z s)

Notice that n 0 Succ = Succ(Succ(....(Succ 0)...)) = n. That is, if we apply our encoding to the natural number 0 and the successor function we get the natural number n. In general it is useful to think of n z s in an expression as standing for applying s to z a total of n times.

With this understanding, the following definition of addition should make sense:

   Plus = λm.λn.λz.λs.m (n z s) s

In the body of Plus, the term n z s represents applying s to z a total of n times. Thus m (n z s) s represents applying s a total of m times to a term which already has s applied to z a total of n times. Thus we have a total of m+n applications of s to z

Exercise: Prove by induction on m, that Plus m n = m+n.

CS441 | CS Department | Princeton University

Princeton University Computer Science Dept.

Computer Science 441 Programming Languages Fall 1998 Lecture 5