COS 402: Artificial
Intelligence
Programming
Assignment
|
Fall 2016
|
Implementing MCMC
Automobile insurance
The code we are
providing
The code that you need to write
What to turn in
This assignment is about using the Markov Chain Monte Carlo technique for approximate inference in Bayes nets. The main components of the assignment are the following:
- Implement the MCMC algorithm.
- Test the MCMC algorithm on a number of Bayes nets.
Implementing
MCMC for Bayes Nets
The first part of the assignment is to implement the MCMC algorithm, Gibbs sampling, which is a special case of the Metropolis-Hastings algorithm covered in class. Instead of sampling a value based on the ratio of the probability of next state to the probability of the current state, Gibbs sampling samples a value for the selected non-evidence variable from the conditional probability distribution of Xj given the settings of all other variables. The purpose of this algorithm is to estimate the probability distribution of one variable in a Bayes net, given the settings of a subset of the other variables. As described below, we are providing code for reading in a Bayes net and a query to the Bayes net. A query is a probability distribution of a variable given settings of some other variables. Your code should then run MCMC some specified number of iterations to estimate the required probability.
Since MCMC is a randomized, iterative algorithm, the actual number of iterations needed to estimate probabilities is an important (and not fully understood) issue, and one that will be explored as part of this assignment.
Sampling from a probability distribution: For one part of the MCMC algorithm, you will need to sample randomly from an arbitrary distribution over a small set of possible values. Here is a simple way to do this, given access to the kind of (pseudo-)random numbers provided by Java. Suppose we want to choose among four values, A, B, C and D, and suppose further that we want to pick A with probability 0.22, B with probability 0.43, C with probability 0.05 and D with probability 0.30. In Java, it is possible to obtain (approximately) uniformly distributed random numbers in the range [0, 1), where [a, b) denotes the set of real numbers bigger than or equal to a, and (strictly) smaller than b. Let r be such a random number. Then, to sample according to the given distribution over A, B, C and D, we just need to pick A if r is in [0.00, 0.22), B if r is in [0.22, 0.65), C if r is in [0.65, 0.70), and D if r is in [0.70, 1.00). Because r is equally likely to be any real number in [0,1), the chance of choosing each of the four values is simply equal to the length of the interval that we associated with it (for instance, the chance of choosing B is the length of the interval [0.22, 0.65), which is 0.43). Thus, each of the four values will be selected with exactly the desired probability.
If implemented properly, this procedure, when selecting randomly among k values, can be made to run in O(k) time. For generating random numbers, see the documentation for the Random class which is provided as part of the Standard Java Platform. Specifically, you should use the nextDouble() method.
Recall that for Bayes nets, some variables are hidden and some are fixed, also called evidence variables.
Which variation of MCMC to use: There are many ways to implement the "Search Rule" for MCMC. For this assignment, please use the random-update version, in which a single randomly selected non-evidence variable Xj is updated on each iteration (where each non-evidence variable is chosen with equal probability), and then you need to sample a value for Xj randomly from the conditional probability distribution of Xj given the settings of all other variables. Also, your estimated probability distribution should be based on all iterations of the algorithm.
Once your MCMC implementation is working and has been tested for correctness, the second part of the assignment is to try it out on a number of Bayes nets and queries, some of which we are providing, and others that you are asked to create.
The next Bayes net attempts to estimate the risk posed by an individual seeking car insurance. In other words, the network attempts to relate variables like the age and driving history of the individual to the cost and likelihood of property damage or bodily injury. Here is a graphical depiction of the network:
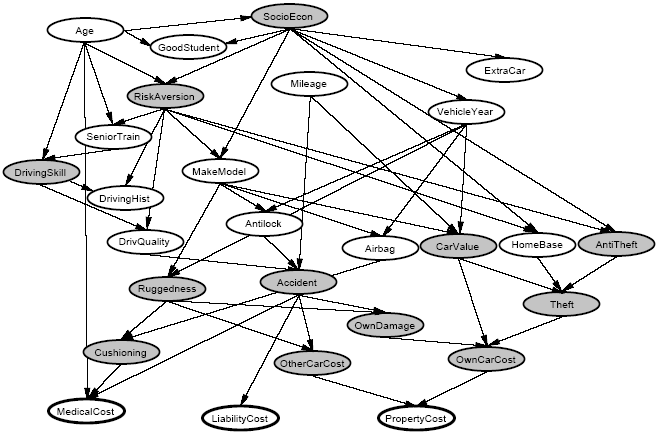
The 12 shaded variables are considered hidden or unobservable, while the
other 15 are observable. The network has over 1400 parameters. An insurance
company would be interested in predicting the bottom three "cost"
variables, given all or a subset of the other observable variables. For
instance, for an adolescent driving a car with about 50,000 miles and no
anti-lock brakes, we can estimate the cost of property damage to have the
following distribution:
|
Estimated Cost |
Probability |
|
$1,000 |
0.457 |
|
$10,000 |
0.343 |
|
$100,000 |
0.173 |
|
$1,000,000 |
0.028 |
The network has been provided in the file insurance.bn.
- The query above (the probability distribution of the
cost for an adolescent driving a car with about 50,000 miles and no
anti-lock brakes) is provided in the file insurance1.qry. Run MCMC on this
query for enough iterations that you are
convinced that it has converged (say, to a value that is correct to two
significant digits of the true probability). For instance, you might print
out the answer, say, every 1000 iterations, and watch until it seems that
the estimated probabilities are not changing significantly. What answer
did you get? How many iterations did you need?
Print out 10 last answers in your report.
- Try out at least one other query of your own invention
using MCMC, and report the results. For instance, you might see what
happens when it is learned that the driver above has an excellent or very
poor driving record. Or you can try out entirely different
queries. (Note that, unless you have a good reason for doing so,
your queries should not involve hidden variables.) Call your query
file(s) insurance2a.qry, insurance2b.qry, etc. Describe
what you tried and what results you got. Comment on why your results
did or did not make sense, and how they reflect realistic or unrealistic
assumptions that have been built into the network.
Next, we will explore the convergence properties of MCMC on a very simple family of Bayes nets. Theoretically, MCMC will converge to the right answer asymptotically, that is, as the number of iterations becomes very large. However, in practice, it is not always clear how many iterations actually suffice, as this example demonstrates.
Each network in this family has a single "leader" variable, and some number of "follower" variables. The idea is that the leader selects a bit at random (0 or 1 with equal probability), and then all of the followers choose their own bits, each one copying the leader's bit with 90% probability, or choosing the opposite of the leader's bit with 10% probability. (For instance, to be concrete, the "leader" might be President Eisgruber, and the "followers" might be members of the university's Board of Trustees; the bits then might represent voting for or against a particular motion. We are assuming that each of the board members follows President E.'s lead in how they vote on this motion with 90% probability.)
Here is the topology of such a network with four followers:

Leader-follower networks with k followers have been provided in the files leader-follower-k.bn for k = 5, 10, 15, 20, 25, 30, 35, 50.
The query we will study in each case is rather trivial: We will simply ask what the (marginal) probability distribution is for the leader variable, in the absence of any evidence (i.e., none of the other variables have been set to specified values). This query is encoded in the file leader-follower.qry.
Here are things to try and questions to answer:
- What is the correct answer for the query given
above? (This should not be difficult to answer.)
- Run MCMC on a network with 10 followers using the given
query. Run for at least 100 million (108) iterations,
printing the partial results at least every 100,000 iterations. Make
a plot of the estimated probability (as estimated by MCMC) of the leader
choosing the bit 0 as a function of the number of iterations executed by
MCMC. (In other words, the x-axis gives the number of iterations
t, and the y-axis gives the probability of the leader bit
being 0 as estimated after t iterations of MCMC.) Does MCMC
seem to converge to the right answer? If so, roughly how long does
it seem to take? (You can use any standard graph plotting software,
such as gnuplot, excel or matlab.)
- Now repeat the last question on networks with 25
followers and 50 followers. Run for at least a billion (109)
iterations, printing partial results at least every million (106)
iterations.
- Can you explain what you observed? Why does MCMC
have such a hard time with these networks? What do these experiments
say about the difficulty of detecting convergence?
The code we are providing
We are providing a class called BayesNet for reading in a description of a Bayes net from a data file. A description of the topology of the Bayes net is stored in public fields of the BayesNet object, while the conditional probability tables are accessed using a public method. Internally, variables are identified with the integers 0, 1, 2, ..., up to (but not including) the number of variables. The values that each variable can take are also given as integers in a similar manner. Here are the public fields of a BayesNet object: numVariables is the number of variables; varName[i] is the name (as a String) of variable i; numValues[i] is the number of values that variable i can take, and valueNames[i][j] gives the name of variable i's j-th value; numParents[i] is the number of parents of variable i; and parents[i][] is an array listing the parents of variable i.
Access to the conditional probabilities which define the Bayes net is via the public method getCondProb(). This method returns the conditional probability of a specified variable x taking a particular value, given the settings of variable x's parents. The first argument to this method is simply the variable x whose (conditional) probability is to be looked up. The second argument vals[] is an integer array of length equal to the total number of variables, where vals[i] is a provided value for variable i. Values must be provided in this array for x and for all of x's parents; all other values in this array will be ignored. The value returned by the method is the conditional probability of variable x taking the value vals[x], given that all of x's parents are set to the values specified in the vals[] array.
A BayesNet object can be constructed using a constructor which takes as argument the name of the file containing a description of the Bayes net. These files should have a format like this one, alarm.bn, which encodes the "burglar alarm" network (R&N Figure 14.2):
variable Burglary t f
variable Earthquake t f
variable Alarm t f
variable JohnCalls t f
variable MaryCalls t f
probability Burglary
0.001 0.999
probability Earthquake
0.002 0.998
probability Alarm | Burglary Earthquake
t t 0.95 0.05
t f 0.94 0.06
f t 0.29 0.71
f f 0.001 0.999
probability JohnCalls | Alarm
t 0.90 0.10
f 0.05 0.95
probability MaryCalls | Alarm
t 0.70 0.30
f 0.01 0.99
The first line specifies the name of a variable called "Burglary" which can take two values called "t" and "f". Throughout the program, the ordering of the values of this variable should follow the ordering given here in the .bn file; thus, in this case, "t" will be associated with value 0 for the Burglary variable, and "f" with value 1. The next several lines in the first block similarly define variables and their values.
The next block (beginning "probability
Burglary") specifies the probability of each of Burglary's two values: t has probability 0.001 and f has probability 0.999. Note that,
because Burglary has no parents,
nothing follows the word "Burglary"
in this block. Skipping ahead, the fourth block (beginning "probability Alarm") specifies that
variable Alarm's parents are Burglary and Earthquake. The lines that follow within this block
define Alarm's conditional
probability table. For instance, the second line gives the probability
distribution of Alarm when Burglary is set to value
MCMC can have difficulties when the conditional probability tables include probabilities that are equal to zero since this can cause the variables to be initialized to values that would actually be impossible (i.e., have zero probability), which in turn can lead to, for instance, division by zero problems when updating the values of non-evidence variables. To avoid these difficulties, when zero probability values are read in from a file describing a Bayes net, the BayesNet code replaces all such values by a tiny positive constant, say, 1e-50. (In fact, any value smaller than this constant gets replaced.)
We also are providing a Query class for reading in queries from files or from standard input. The query itself is stored in public fields of the Query object. Queries are always of the form: what is the probability distribution of some particular variable, given the settings of some other variables (the so-called evidence variables)? Accordingly, Query objects have two public fields: queryVar is the variable whose value is being queried, and evidence[] is an array specifying the settings of a subset of the other variables. More specifically, evidence[i] gives the value that variable i is to be set to if it is one of the evidence variables for this query; otherwise, if variable i is not an evidence variable, then evidence[i] is set to -1.
Here is an example file, alarm1.qry, showing the format of query files:
Burglary
JohnCalls t
MaryCalls t
The first line specifies the query variable. Each of the subsequent
lines specifies an evidence variable and the value to which it should be
set. This particular query asks for the probability distribution of the
The class RunMcmc provides a main that you can use for testing, or you may wish to write your own (although it is still required that your code work with the main that we provided). Once MCMC has been implemented, this main simply runs MCMC for some number of rounds, printing partial results with a specified frequency, on a given Bayes net and query. For instance, the following command might produce the following output (of course, the output will be different each time that the algorithm is run since MCMC is a randomized algorithm):
> java RunMcmc alarm.bn alarm1.qry 100 20
20 0.85000000 0.15000000
40 0.47500000 0.52500000
60 0.31666667 0.68333333
80 0.37500000 0.62500000
100 0.37000000 0.63000000
>
The command-line arguments are: name of the file describing the Bayes net; name of the file describing the query; maximum number of iterations; frequency with which results should be printed. Here, the specified Bayes net and query correspond to the example files given above. The first line of the output means that, after 20 iterations, the estimated probability that Burglary equals t or f is 0.85 or 0.15, respectively. Similarly for the lines that follow.
The code and all data files are available as a single zip file here. Data is included in the data subdirectory. Documentation on the provided Java classes is available here.
As a general reminder, you should not modify any of the code that we are providing, other than template files, or unless specifically allowed in the instructions. You also should not change the "signature" of any of the methods or constructors that you are required to write, i.e., the parameters of the method (or constructor), their types, and the type of the value returned by the method.
The code that you need to write
Your job is to fill in the MCMC algorithm in the template file Mcmc.java. You need to first fill in a constructor which will take as input a BayesNet and Query, and which will initialize all data structures you are using appropriately, but which will not actually run MCMC. You then need to fill in the method runMoreIterations(). This method takes an integer argument specifying how many additional iterations of MCMC are to be executed. So, calling the constructor does not run MCMC, but only sets everything up. Calling runMoreIterations(1000), for instance, would run MCMC for 1000 iterations. Calling runMoreIterations(1000) again would run MCMC for an additional 1000 iterations. It is therefore imperative that you save the state of the current run of MCMC between calls to runMoreIterations(); do not re-start your run of MCMC each time that this method is called.
Each call to runMoreIterations() should return a double array specifying the probability distribution over the values of the query variable.
What
to turn in
Using this DropBox link, you should turn in the following electronically:
- The class Mcmc.java with the constructor
and the runMoreIterations() method filled in.
- Any query files that you created, including at a
minimum: insurance2a.qry.
- If appropriate, a readme.txt
file explaining briefly how your code is organized, what data structures
you are using, or anything else that will help the graders understand how
your code works and is organized.
In addition, you should submit a hard copy containing all of the following:
- The java code you wrote
(Mcmc.java)
- Any query files that you created, including at a
minimum: insurance2a.qry
- Your answers to all of the questions above.
- Any plots that you made (clearly annotated).
Acknowledgments
The (fictional) insurance network was extracted from the paper "Adaptive Probabilistic Networks with Hidden Variables" by J. Binder, D. Koller, S. Russell and K. Kanazawa (Machine Learning, 29, 213?244 (1997)).