Write a program that produces pseudo-random bits by simulating a linear feedback shift register, and then use it to implement a simple encode/decode facility for photographs.

LFSR review.  A linear feedback shift register is a register of bits that performs discrete step operations that

• shift all the bits one position to the left and
• replace the vacated bit by the exclusive or of the bit shifted off and the bit at a given tap position in the register.

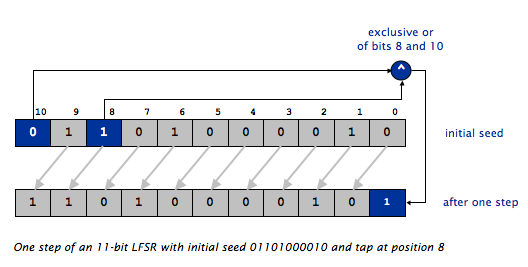
A LFSR has three parameters that characterize the sequence of bits it produces: the number of bits N, the tap position tap, and the initial seed (the sequence of bits that initializes the register). As in the example in Lecture 1, the following gives the contents of the LFSR with initial seed 01101000010 and tap position 8 after one step.

Simulate a LFSR.  Your first task is to write a class that simulates the operation of a LFSR by implementing the following API:

public class LFSR
-------------------------------------------------------------------------------------------------------------------
       LFSR(String seed, int tap)  //  create LFSR with the given initial seed and tap
   int step()                      //  simulate one step and return the least significant (rightmost) bit as 0 or 1
   int generate(int k)             //  simulate k steps and return k-bit integer
String toString()                  //  return a string representation of the LFSR

To implement LFSR you need to choose the internal representation (instance variables) and to implement the constructor and three methods in the API. These are all interrelated, and there are several possible approaches.

• Constructor. For simplicity, the constructor takes the initial seed as a String whose characters are all 0 or 1. The length of the register is the length of the seed. We will generate each new bit by xoring the most significant (leftmost) bit and the tap bit. The position of the tap bit comes from the constructor argument. For example, the following code should create the LFSR described above.

  LFSR lfsr = new LFSR("01101000010", 8);
  

• String representation. The toString() method should return a string representation of the LFSR by concatenating the values in the registers. For example,

  LFSR lfsr = new LFSR("01101000010", 8);
  System.out.println(lfsr);
  

  should output

  01101000010
  

• Simulate one step. The step() method simulates one step of the LFSR and returns the least significant (rightmost) bit as an integer (0 or 1). For example,

  LFSR lfsr = new LFSR("01101000010", 8);
  for (int i = 0; i < 10; i++) {
      int bit = lfsr.step();
      System.out.println(lfsr + " " + bit);
  }
  

  should output

  11010000101 1
  10100001011 1
  01000010110 0
  10000101100 0
  00001011001 1
  00010110010 0
  00101100100 0
  01011001001 1
  10110010010 0
  01100100100 0
  

• Extracting multiple bits.  The method generate() takes an integer k as an argument and returns a k-bit integer obtained by simulating k steps of the LFSR. This task is easy to accomplish with a little arithmetic: initialize a variable to zero and, for each bit extracted, double the variable and add the bit returned by step(). For example, given the bit sequence 1 1 0 0 1 the variable takes the values 1, 3, 6, 12, 25, ending with the binary representation of the bit sequence.

  LFSR lfsr = new LFSR("01101000010", 8);
  for (int i = 0; i < 10; i++) {
      int r = lfsr.generate(5);
      System.out.println(lfsr + " " + r);
  }
  

  should output

  00001011001 25
  01100100100 4
  10010011110 30
  01111011011 27
  01101110010 18
  11001011010 26
  01101011100 28
  01110011000 24
  01100010111 23
  01011111101 29
  

  Note: The easiest way to implement the generate() method is to call the step() method k times.

A client to encrypt and decrypt images.  Your next task is write a LFSR client PhotoMagic.java that can encrypt images. PhotoMagic should take three command-line arguments, an image name, a binary password (an initial LFSR seed), and a tap number. It should save an encrypted image in a file named by prepending an X to the given file name (use the save() method in the Picture class). It should also show the encrypted image on the screen (use the show() method, also in the Picture class). For example, typing

% java PhotoMagic pipe.png 01101000010100010000 16

takes as input the image on the left below and produces the image (in a file) on the right below.

	pipe.png	Xpipe.png

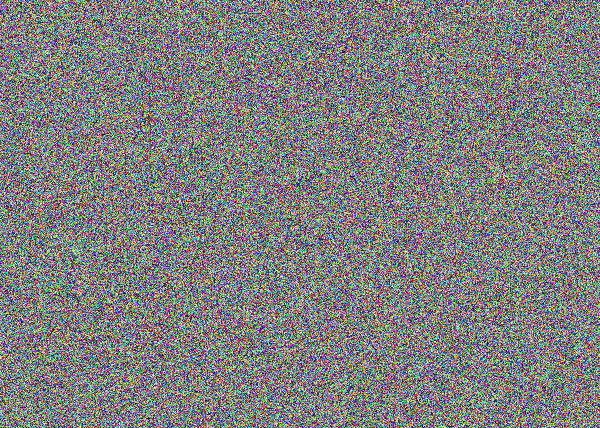
Important notes: We use the .png format because it is a lossless format that preserves the precise bits in the colors. Also, it is best to use a password (and LFSR) that is longer than 12 bits because images have a large number of bits and also because our use of fixed tap position (such as 8) per run does not guarantee that the register will cycle through all values for all lengths. You might enjoy experimenting with violating these rules.

Implementing PhotoMagic is the easiest part of this assignment. It can be accomplished by a few additions and changes to Grayscale.java (Program 3.1.4 of the book), which relies on the Picture.java data type (Section 3.1). For each pixel (x, y), in the order (0, 0), (0, 1), (0, 2), ..., extract the red, green, and blue components of the color (each component is an integer between 0 and 255). Then, xor the red component with 8 newly generated bits. Do the same for the green (using another 8 newly generated bits) and, finally, the blue. Create a new color using the result of the xor operations, and set the pixel to that color.

Now, here's the magic: If you understood Lecture 1, you know that running the same program with the same password on this picture recovers the original image!

% java PhotoMagic Xpipe.png 01101000010100010000 16

will produce the following result.

	Xpipe.png	XXpipe.png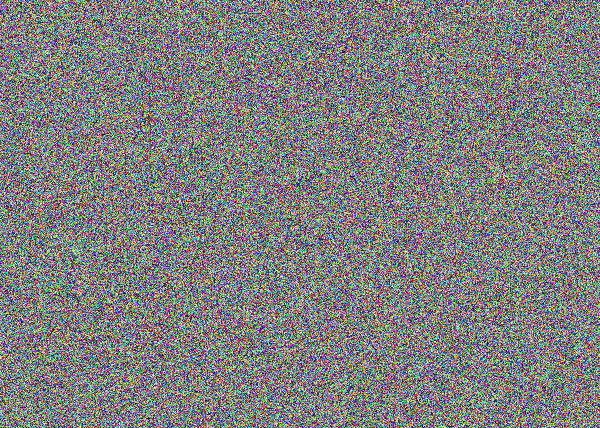

Getting started. The subdirectory lfsr from the COS126 ftp site contains a template LFSR.java file to get you started. It also contains Picture.java, pipe.png, Xbaboon-red.png, Xscarpet-cookies.png and this assignment's readme.txt file.

Picking a good tap number. Here are suggested tap numbers for maximizing the cycle of different size binary registers: 5 bits, tap 2; 6 bits, tap 4; 9 bits, tap 4; 10 bits, tap 6; 11 bits, tap 8; 20 bits, tap 16; 30 bits, tap 22; 36 bits, tap 24; 48 bits, tap 42.

Submission.   Submit LFSR.java and PhotoMagic.java. Also, submit a readme.txt file and answer the questions.

Midterm Evaluation.  Please fill out the following anonymous questionnaire to provide us with feedback to help us improve this course.

Extra Credit.  Using a binary password is weak protection (see Challenge for the Bored) and inconvenient, so create a PhotoMagicDeluxe.java implementation to take an alphanumeric password. To avoid problems with special characters, use a six-bit code where the ith character in the string

"ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/" 

Your PhotoMagicDeluxe program should take three command-line arguments: an image name, an alphanumeric password, a tap number. Like PhotoMagic.java, it should show the encrypted image and save that image in a file named by prepending an X to the input file name.

Note for Extra Credit.  Work modularly. Don't just copy huge sections of your homework code into your extra credit program. Have your Extra Credit client call any methods it needs to use. Yes, you can call any public method from another class.

Challenge for the bored.  Assume that you know the password has N bits (where N is the second command-line argument). Write a program BreakPhotoMagic.java that tries all possible seeds and all possible taps and finds the picture. Hint: all but the correct seed and tap will produce pseudo-random colors, so you can track the frequencies of each 8-bit value and pick the seed and tap that results in the frequencies that deviate the most from 128.

Warning: this program can take a very long time to run, so you want to debug it using small passwords with only 5 or 6 bits (even though 5 or 6 bits is not long enough to generate a very good encryption).