

The original "killer app" for personal computers was an Apple II program called VisiCalc, written in 1978 by Dan Bricklin and Bob Frankston. VisiCalc made it possible to use a computer for the kind of analyses that generations of business people had previously done by hand with paper "spreadsheets": rows and columns of related numbers that could be used to organize data and assess alternatives in a systematic way.
Today, spreadsheets are the quantitative reasoning tool for many people. In terms of market share, Microsoft's Excel is the de facto standard, with Lotus 1-2-3 (the lineal descendant of VisiCalc) a distant second choice; there are also free open-source spreadsheets like Gnumeric and OpenOffice Calc, and Google has a web-based spreadsheet. All such programs have a common computational model and similar visual appearance, however, and although we will use Excel in this lab, whatever you see will transfer in spirit, though not in detail, to the others. We're also using the Windows version; the Mac version of Excel is quite similar, so you should be able to do this lab on a Mac without major changes.
Excel is enormously powerful and complicated, so we will investigate only a tiny fraction of its features. As you work through the specific instructions in this lab, take time to leave the official track and experiment on your own with anything that looks interesting. There's little risk in this: Excel's Undo and Redo feature let you back out of something that went wrong, or repeat the steps that got you someplace interesting. Undo and Redo are the small curved arrows near the middle of this screenshot:

If you want to know more about Excel, there are many hundreds of books, some good, and many web pages. The party line is found at Microsoft's Excel site, while John Walkenbach's spreadsheet page provides independent material from the author of several good books.
Part 1: Cells and Formulas
Part 2: Ranges and Functions
Part 3: Importing and Graphing Data
Part 4: How to Lie with Statistics (1)
Part 5: How to Lie with Statistics (2)
Part 6: Submitting your work

Take some time now to explore the menus, toolbars, and the like.
The individual elements of a spreadsheet are called cells. A cell is identified by its row and column; thus the cell in the upper left corner (highlighted when you started Excel) is named A1. The highlighted cell is called the active cell.
Cells can contain numbers (the most common case) or text, and their values can be set by what you type into them, loaded from files or the Internet, or computed by a formula that derives a value from the values of other cells.
Time to do some experimenting.
You can change the format of cell data by "Format | Cells", and then select "Number" to set the numeric display, "Alignment" to control centering, "Font" to set size and color, and so on. The most common reason to adjust cell format is to cause data to be treated as numeric and displayed with the same number of significant digits, or to define the format for data that represent dates. You can instead put text in cells to serve as headings for columns or rows; text can be set in various sizes and fonts as well.
You can use commands under "Edit" to clear cell contents entirely. In all of these, you can select a single cell, a group of cells, one or more entire rows, or one or more entire columns; the action applies to the selected range.
To insert an additional row or column, highlight the row or column before which you want to insert, then use the "Insert" menu.
A formula is typed into a cell just like data except that the first character must be an equals sign =. To experiment with this:
A further experiment:
It takes a lot of typing to enter data values and formulas this way, so Excel provides some convenient shortcuts.
Finally,
Excel, like Word, uses Visual Basic as a scripting language. All of Excel's myriad capabilities (including anything you can do with keyboard and mouse) are accessible from VB code. This can be used to organize much more complicated computation than would be feasible with simple formulas in cells, to tailor the interface for specific purposes, and to access all of the repertoire of other components on Windows. And of course the bad news is that spreadsheets can be just as much carriers of VB-based viruses as Word documents, so you should run Excel with macros disabled by default.
We won't pursue any of this further, but if you want to explore, VB is waiting for you: Tools / Macro / VB Editor.... One of the neatest features is that you can turn on the "macro recorder"; this will record whatever subsequent actions you perform and convert them into the equivalent VB code. It's a very effective learning tool and a valuable complement to the manual.
The rule of 72 tells you how to estimate the doubling time approximately: divide 72 by the interest rate, and that's the number of periods. So at 10% per year, the doubling time is about 7.2 years. If the interest rate is only 6%, the doubling time is about 12 years. Of course, you can turn it around: divide 72 by the number of periods and it gives the interest rate. Consider Moore's Law, that the capacity of semiconductor chips doubles every 18 months. By the Rule of 72, we see that capacity is compounding at about 72/18 = 4% per month.
The approximation isn't perfect, but it's pretty accurate for the kinds of percentages found in daily life for home mortgage interest rates, bond interest, car payments, tuition increases, and so on. If you want to see how it works, Google provides lots of hits; this one is pretty clear.
Your task is to make a spreadsheet that shows how good the approximation is for a variety of interest rates.
|
Try to do this with as little typing and as much use of Excel's extension feature as possible. Your table should look like this when done:

The rule shows further doublings as well; for instance, note that at 8%, one doubling takes 9 years, and the next takes another 9 years -- that is, 18 years doubles twice, or a factor of four. Check some of the other entries for similar consistency.
In this lab, you will be using a new sheet for each part, each with its own name. For this part,
|
You'll be updating this file throughout the labs, so be sure to save regularly.
For example, A1:A10 describes a column range 10 cells high but only one cell wide. The range B2:K2 represents a row of 10 cells starting at B2, and A1:J10 represents an array of 100 cells, 10 by 10, that starts in the upper left corner. As a special case, A2:A2 is a range that consists of a single cell, and that can be abbreviated to the familiar A2.
Excel provides more complicated ranges, but for the most part, simple rectangular arrays are all we need. It is also possible to name a range, which is easier to understand and refer to in a big spreadsheet; we won't be using that facility here.
The range notation gives us a way to specify an arbitrarily large group of cells, and thus write out computations more compactly and clearly. For instance, it's impractical to type a formula like =A1+A2+A3+... if there are more than a few terms in the summation; a range is a lot easier.
Excel provides a great number of mathematical functions that perform operations over a range of cells. The simplest of these is sum, which adds up the numbers in a range: the formula =SUM(range) produces the sum of the values in the cells in the specified range.
What happens if you need another row or column, because your data set has expanded? If you insert a row or a column within a range, Excel is pretty clever about guessing what you mean, and will extend the formula for you. But if you add a row or column at one end of the range, Excel isn't sure what you had in mind, and doesn't change the formula. Verify this behavior:
The task is to generate a table that displays stock prices and relative performance for two stocks for the past two or three months. You can choose any two stocks you like. We looked at Cisco vs. Microsoft in class; other interesting pairs might be selected from among Amazon, Ebay, Google, Yahoo, IBM, Oracle, Ford, GM, etc. Here we will just call the two stocks FOO and BAR.

Now merge the two data sequences into one sheet:
The prices are in most recent first order, which is wrong for graphing. Reverse them:
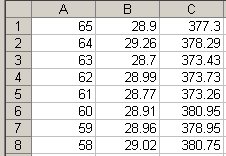
At this point, if you select columns B and C, you can produce a graph that compares the two stocks, but it won't be very interesting if their prices differ by too much, as in the table above. So the next step is to make two new columns that show how the prices have changed in proportion to the first value.
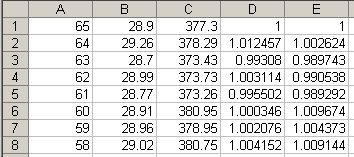

|
Now transfer the data and the graphs to your lab7.xls. (This assumes that you are also running Excel on lab7.xls.)
|

Or did they? These are examples of what Darrell Huff, in the wonderful book How to Lie with Statistics, calls the Gee-Whiz Graph, a form of statistical chicanery that is all too common in newspapers (even the Prince!) and magazines. (Six months later, the Times printed an article decrying the practice, though without acknowledging how often they did it themselves; their subsequent charts have on average been much better.)
Gee-whiz graphs are deceptive because they use the entire chart area to give the impression of a big change. This gives entirely the wrong impression when not much is happening and it makes comparisons quite misleading. Consider TRW versus Corel. TRW seems to have risen a bit more than Corel, at least graphically, but in fact their fortunes were enormously different: TRW rose a modest 3%, while Corel went up by 78%! Similarly, one could easily conclude that GE went down more than HealthSouth, but in fact, the declines are 6.5% and 55%. (This was about the beginning of a decline for HealthSouth as more and more fraud was uncovered in their accounting.)
The heart of the deception is plotting a graph that doesn't include the full range of data. Each graph should be plotted with the Y axis beginning at zero; that would give a much more accurate sense of the magnitude of the change. And then if each is plotted with a comparable upper bound, somewhat above the largest data value, that makes it possible to compare the two graphs in a meaningful way.
Your task is to produce two sensible graphs that permit such a fair comparison, by having the Y axis start at 0 and the values just about fill the vertical range, like this graph of the Corel data:

Note that the data in these text files is in the wrong order; use Excel's sorting capabilities (e.g., Data | Sort...) to get it into the right order.
|
It's always nice when others recognize one's true greatness, as US News and World Report has done every year since 2000:

But how are these rankings really determined? And just how much do they really mean?
US News explains their methodology. They collect data on a variety of factors for each school, weight the factors according to how important they seem, and then sort the results. For example, "peer assessment" accounts for 25% of the score, "student selectivity" for 15% (half of that is SAT scores), and alumni giving percentage for 5%. Princeton ties with Harvard on the first, is behind on the second, and wins big on the third. So if only SAT scores mattered, Princeton would be further down. (The details change from year to year, and each year US News becomes more circumspect about revealing anything.)
There are at least two problems with these ranking schemes: the data itself is suspect, and the weighting factors are arbitrary. (We pass over how schools themselves might try to game the system, a tactic that is not unheard of.) In this lab, we'll accept the data values, however flaky they might be, and focus on the weighting factors.
The file usnews2004.xls contains some carefully fiddled data and a set of weights, loosely based on the data from 2004, that almost preserve the 2004 ordering; many factors have been unceremoniously dropped and a few data values have been adjusted, so don't read anything into this, especially not about the merits of individual schools then or now. Here is the display:
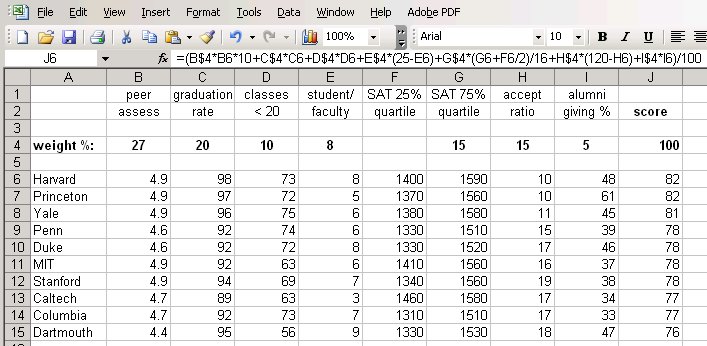
The first two rows show the factors, and the fourth row gives weights that sum to 100% (cell J4). The range J6:J15 shows the computed scores. The formula box shows the formula being used to compute J4; subsequent rows have the same formula except for cell references. A couple of factors are combined (SAT) or complemented (acceptance rate); for instance a low acceptance rate is deemed better than a high acceptance rate.
Your task is to find several sets of non-negative weights that will rearrange the schools in various ways. Note that the weights in B4:I4 must sum to 1.
|
Give this a decent effort, not just the first obvious thing that happens to make a change. You should also experiment with Excel's sorting capabilities here; at the end, you should be able to sort the schools by any combination of factors, for example, by decreasing reputation score and within that by increasing acceptance rate.
At this point you should have a workbook with four sheets: Rule72, Stocks, Lies, Rank. Check through them to make sure they look right.
When you are absolutely sure that you have all the individual sheets in lab7.xls and have saved it on your network drive, send email to cos109@princeton.edu, with lab7.xls as an attachment. The subject of the message should be "Lab 7 - Your Name".